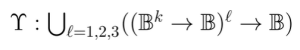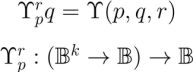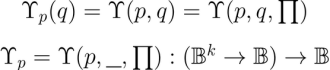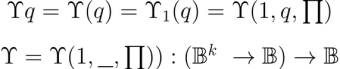The “pragmatic maxim”, also known as the “maxim of pragmatism” or the “maxim of pragmaticism”, is a maxim of logic formulated by Charles Sanders Peirce. Serving as a practical recommendation or regulative principle in the normative science of logic, its function is to guide the conduct of thought toward the achievement of its purpose, advising the addressee on an optimal way of “attaining clearness of apprehension”.
Peirce stated the pragmatic maxim in many different ways over the years, each of which adds its own bit of clarity or correction to their collective corpus.
-
The first excerpt appears in the form of a dictionary entry, intended as a definition of pragmatism.
Pragmatism. The opinion that metaphysics is to be largely cleared up by the application of the following maxim for attaining clearness of apprehension:
“Consider what effects, that might conceivably have practical bearings, we conceive the object of our conception to have. Then, our conception of these effects is the whole of our conception of the object.” (Peirce, CP 5.2, 1878/1902).
-
The second excerpt gives another version of the pragmatic maxim, a recommendation about a way of clarifying meaning that can be taken to stake out the general philosophy of pragmatism.
Pragmaticism was originally enounced in the form of a maxim, as follows: Consider what effects that might conceivably have practical bearings you conceive the objects of your conception to have. Then, your conception of those effects is the whole of your conception of the object.
I will restate this in other words, since ofttimes one can thus eliminate some unsuspected source of perplexity to the reader. This time it shall be in the indicative mood, as follows: The entire intellectual purport of any symbol consists in the total of all general modes of rational conduct which, conditionally upon all the possible different circumstances and desires, would ensue upon the acceptance of the symbol. (Peirce, CP 5.438, 1878/1905).
-
The third excerpt puts a gloss on the meaning of a practical bearing and provides an alternative statement of the maxim.
Such reasonings and all reasonings turn upon the idea that if one exerts certain kinds of volition, one will undergo in return certain compulsory perceptions. Now this sort of consideration, namely, that certain lines of conduct will entail certain kinds of inevitable experiences is what is called a “practical consideration”. Hence is justified the maxim, belief in which constitutes pragmatism; namely:
In order to ascertain the meaning of an intellectual conception one should consider what practical consequences might conceivably result by necessity from the truth of that conception; and the sum of these consequences will constitute the entire meaning of the conception. (Peirce, CP 5.9, 1905).
-
The fourth excerpt illustrates one of Peirce’s many attempts to get the sense of the pragmatic philosophy across by rephrasing the pragmatic maxim in an alternative way. In introducing this version, he addresses an order of prospective critics who do not deem a simple heuristic maxim, much less one that concerns itself with a routine matter of logical procedure, as forming a sufficient basis for a full-grown philosophy.
On their side, one of the faults that I think they might find with me is that I make pragmatism to be a mere maxim of logic instead of a sublime principle of speculative philosophy. In order to be admitted to better philosophical standing I have endeavored to put pragmatism as I understand it into the same form of a philosophical theorem. I have not succeeded any better than this:
Pragmatism is the principle that every theoretical judgment expressible in a sentence in the indicative mood is a confused form of thought whose only meaning, if it has any, lies in its tendency to enforce a corresponding practical maxim expressible as a conditional sentence having its apodosis in the imperative mood. (Peirce, CP 5.18, 1903).
-
The fifth excerpt is useful by way of additional clarification, and was aimed to correct a variety of historical misunderstandings that arose over time with regard to the intended meaning of the pragmatic maxim.
The doctrine appears to assume that the end of man is action — a stoical axiom which, to the present writer at the age of sixty, does not recommend itself so forcibly as it did at thirty. If it be admitted, on the contrary, that action wants an end, and that that end must be something of a general description, then the spirit of the maxim itself, which is that we must look to the upshot of our concepts in order rightly to apprehend them, would direct us towards something different from practical facts, namely, to general ideas, as the true interpreters of our thought. (Peirce, CP 5.3, 1902).
-
A sixth excerpt is useful in stating the bearing of the pragmatic maxim on the topic of reflection, namely, that it makes all of pragmatism boil down to nothing more or less than a method of reflection.
The study of philosophy consists, therefore, in reflexion, and pragmatism is that method of reflexion which is guided by constantly holding in view its purpose and the purpose of the ideas it analyzes, whether these ends be of the nature and uses of action or of thought. … It will be seen that pragmatism is not a Weltanschauung but is a method of reflexion having for its purpose to render ideas clear. (Peirce, CP 5.13 note 1, 1902).
-
The seventh excerpt is a late reflection on the reception of pragmatism. With a sense of exasperation that is almost palpable, Peirce tries to justify the maxim of pragmatism and to correct its misreadings by pinpointing a number of false impressions that the intervening years have piled on it, and he attempts once more to prescribe against the deleterious effects of these mistakes. Recalling the very conception and birth of pragmatism, he reviews its initial promise and its intended lot in the light of its subsequent vicissitudes and its apparent fate. Adopting the style of a post mortem analysis, he presents a veritable autopsy of the ways that the main idea of pragmatism, for all its practicality, can be murdered by a host of misdissecting disciplinarians, by what are ostensibly its most devoted followers.
This employment five times over of derivates of concipere must then have had a purpose. In point of fact it had two. One was to show that I was speaking of meaning in no other sense than that of intellectual purport. The other was to avoid all danger of being understood as attempting to explain a concept by percepts, images, schemata, or by anything but concepts. I did not, therefore, mean to say that acts, which are more strictly singular than anything, could constitute the purport, or adequate proper interpretation, of any symbol. I compared action to the finale of the symphony of thought, belief being a demicadence. Nobody conceives that the few bars at the end of a musical movement are the purpose of the movement. They may be called its upshot. (Peirce, CP 5.402 note 3, 1906).
whenever I ran across it. I suppose that small arc of revolution had been building for years but it struck me as crossing a threshold to a more explicit, self‑conscious stage about that time.
called the umpire operator, which takes 1, 2, or 3 propositions as arguments and returns a single truth value as the result. Operators with optional numbers of arguments are called 
in that form gives the following formula.
evaluates the proposition 
on each model of the proposition 
and combines the results according to the method indicated by the connective parameter 
In principle, the index 
may specify any logical connective on as many as 
arguments but in practice we usually have a much simpler form of combination in mind, typically either products or sums. By convention, each of the accessory indices 
is assigned a default value understood to be in force when the corresponding argument place is left blank, specifically, the constant proposition 
for the lower index 
for the upper index 
if and only if 
In propositional terms, this is tantamount to the assertion that 
or that 
if and only if 
The ambiguities of this usage are not a problem so long as we distinguish the context of definition from the context of application and restrict all shorthand notations to the latter.
Inquiry Into Inquiry 