Peirce’s 1870 “Logic of Relatives” • Comment 8.5

I continue with my commentary on CP 3.73, developing the Othello example as a way of illustrating Peirce’s formalism.

Since multiplication by a dyadic relative term is a logical analogue of matrix multiplication in linear algebra, all the products computed above can be represented by logical matrices, that is, by arrays of boolean coordinate values.  Absolute terms and dyadic relatives are represented as 1-dimensional and 2-dimensional arrays, respectively.

The equations defining the absolute terms are given again below, first as logical sums of individual terms and then as n-tuples of boolean coordinates.

Since we are going to be regarding these tuples as column arrays, it is convenient to arrange them in a table of the following form.

Here are the dyadic relative terms again, followed by their representation as coefficient matrices, in this case bordered by row and column labels to remind us what the coefficient values are meant to signify.

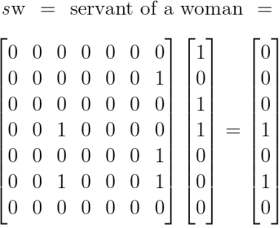
Here are the matrix representations of the products we calculated before.

Resources

• Peirce’s 1870 Logic of Relatives • Part 1 • Part 2 • Part 3 • References

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)