Fourier Transforms of Boolean Functions
Re: Another Problem
The problem is concretely about Boolean functions of
variables, and seems not to involve prime numbers at all. For any subset
of the coordinates, the corresponding Fourier coefficient is given by:
where is
if
is odd, and
otherwise.
Need to play around with this concept a while …
Gaussian Coefficients
The Gaussian coefficient, also known as the q-binomial coefficient, is notated as Gauss(n, k)q and given by the following formula:
(qn−1)(qn−1−1) … (qn−k+1−1) / (qk−1)(qk−1−1) … (q−1).
The ordinary generating function for selecting at most one positive integer is:
1/(1−q) = 1 + q + q2 + q3 + …
The ordinary generating function for selecting exactly one positive integer is:
q/(1−q) = q + q2 + q3 + q4 + …
The ordinary generating function for selecting exactly one positive integer ≥ n is:
qn/(1−q) = qn + qn+1 + qn+2 + qn+3 + …
The ordinary generating function for selecting exactly one positive integer < n is:
q/(1−q) − qn/(1−q) = q + q2 + … + qn−2 + qn−1
(q − qn) / (1 − q) = q + q2 + … + qn−2 + qn−1
(qn − q) / (q − 1) = q + q2 + … + qn−2 + qn−1
The ordinary generating function for selecting at most one positive integer < n is:
(qn − 1) / (q − 1) = 1 + q + q2 + … + qn−2 + qn−1
The ordinary generating function for selecting at most one positive multiple of k is:
1/(1−qk) = 1 + qk + q2k + q3k + …

We have come to a critical point in the arc of democratic societies, where the idea that money can regulate itself, evangelized by the Church of the Invisible Hand, has tipped its hand to the delusion that money itself can regulate society.
Laßt uns rechnen …
One … Two … Three …
— Robert Musil • The Man Without Qualities
eiπ
Benjamin Peirce apparently liked this mathematical synonym for the additive inverse of 1 so much that he introduced three special symbols for e, i, π — ones that enable eiπ to be written in a single cursive ligature, as shown here.
This reminds me of some things I used to think about — I always loved
workingplaying with generating functions and I can remember a time in the 80s when I was very pleased with myself for working out the q-analogue of integration by parts — but it will probably take me a while to warm up those old gray cells today.Let me first see if I can get LaTeX to work in these comment boxes …
The Gaussian coefficient, also known as the q-binomial coefficient, is notated as Gauss(n, k)q and given by the following formula:
(qn−1)(qn−1−1) … (qn−k+1−1) / (qk−1)(qk−1−1) … (q−1).
Groups like acting on the space of
acting on the space of  boolean functions on
boolean functions on  variables come up in my explorations of differential logic.
variables come up in my explorations of differential logic.
Here’s one indication of a context where these groups come up —
Here’s a discussion of the case where
Notes
All Learning Is But Recollection
All Leaning Is But Reïnclination
And they will lean that way forever …
I lean that way myself, inclined to believe
All leaning inclines to preserve the swerve.
If
Then the Shadow falls in a moat
Between the castle of invention
And the undiscovered country.
If
Then the Shadow falls in a moat
Between the castle of invention
And the undiscovered country.
Plato, “Timaeus”, 38 A
Benjamin Jowett (trans.)
Try 9001 and 9002 = 〈 and 〉
Or 12296 and 12297 = 〈 and 〉
⟨ ⟩ = ⟨ ⟩ = ⟨ ⟩
Other possibilities short of using LaTeX —
〈 〉 = 〈 〉
〈 〉 = 〈 〉
If we are thinking about records of a fixed finite length and a fixed signature
and a fixed signature  then a relational data base is a finite subset
then a relational data base is a finite subset  of a
of a  -dimensional coordinate space
-dimensional coordinate space 
Given a non-empty subset of the indices
of the indices ![K = [1, k],](https://s0.wp.com/latex.php?latex=K+%3D+%5B1%2C+k%5D%2C&bg=ffffff&fg=333333&s=0&c=20201002) we can take the projection
we can take the projection  of
of  on the subspace
on the subspace 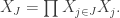
Saying that “a query is likely to use only a few columns” amounts to saying that most of the time we can get by with the help of our small dimension projections. This is akin to a very old idea, having its ancestor in Descartes’ suggestion that “we should never attend to more than one or two” dimensions at a time.
cf. Château Descartes
Just a thought, more loose than lucid most likely —
There is another kind of “discrete logarithm” that I used to call the “vector logarithm” of a positive integer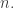 Consider the primes factorization of
Consider the primes factorization of  and write the exponents of the primes in order as a coordinate tuple
and write the exponents of the primes in order as a coordinate tuple 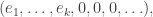 where
where  for any prime
for any prime 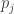 not dividing
not dividing  and where the exponents are all
and where the exponents are all  after some finite point. Then multiplying two positive integers maps to adding the corresponding vectors.
after some finite point. Then multiplying two positive integers maps to adding the corresponding vectors.
Emeticon
http://s583.photobucket.com/user/metasonix/media/vomit.gif.html
[URL=http://s583.photobucket.com/user/metasonix/media/vomit.gif.html][IMG]http://i583.photobucket.com/albums/ss273/metasonix/vomit.gif[/IMG][/URL]
The following tag would normally force invisible borders on a table:
<table border="0" style="border-width:0">But WordPress still leaves a light border line on top of each cell, so you have to add the following parameter to each table datum:
<td style="border-top:1px solid white">Sign relations are just a special case of triadic relations, in much the same way that groups and group actions are special types of triadic relations. It’s a bit of a complication that we participate in sign relations whenever we try to talk about anything else, but it still makes sense to try and tease the separate issues apart as much as we can.
As far as relations in general go, relative terms are often expressed by slotted frames like “brother of __”, “divisor of __”, or “sum of __ and __”. Peirce referred to these kinds of incomplete expressions as rhemes or rhemata and Frege used the adjective ungesättigt or unsaturated to convey more or less the same idea.
Switching the focus to sign relations, it’s a fair question to ask what sorts of objects might be denoted by pieces of code like “brother of __”, “divisor of __”, or “sum of __ and __”. And while we’re at it, what is this thing called denotation, anyway?
It may help to clarify the relationship between logical relatives and mathematical relations. The word relative as used in logic is short for relative term — as such it refers to a piece of language that is used to denote a formal object. So what kind of object is that? The way things work in mathematics, we are free to make up a formal object that corresponds directly to the term, so long as we can form a consistent theory of it, but in our case it is probably easier to relate the relative term to the kinds of relations we already know and love in mathematics and database theory.
In those contexts a relation is just a set of ordered tuples and, if you are a fan of strong typing like I am, such a set is always set in a specific setting, namely, it’s a subset of a specific Cartesian product.
Peirce wrote -tuples
-tuples  in the form
in the form  and referred to them as elementary
and referred to them as elementary  -adic relatives. He expressed a set of
-adic relatives. He expressed a set of  -tuples as a “logical sum” or “logical aggregate”, what we would call a logical disjunction of these elementary relatives, and he frequently regarded them as being arranged in the form of
-tuples as a “logical sum” or “logical aggregate”, what we would call a logical disjunction of these elementary relatives, and he frequently regarded them as being arranged in the form of  -dimensional arrays.
-dimensional arrays.
Time for some concrete examples, which I will give in the next comment …
Table 1 shows the first few ordered pairs in the relation on positive integers that corresponds to the relative term, “divisor of”. Thus, the ordered pair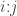 appears in the relation if and only if
appears in the relation if and only if 
Table 2 shows the same information in the form of a logical matrix. This has a coefficient of in row
in row  and column
and column  when
when  , otherwise it has a coefficient of
, otherwise it has a coefficient of  (The zero entries have been omitted here for ease of reading.)
(The zero entries have been omitted here for ease of reading.)
In much the same way that matrices in linear algebra represent linear transformations, these logical arrays and matrices represent logical transformations.
To be continued …
Ð ð
Arrays like the ones sampled above supply a way to understand the difference between a relation and its associated relative terms. To make a long story short, we could say that a relative term is a relation plus an indication of its intended application. But explaining what that means will naturally take a longer story.
In his first paper on the “Logic of Relatives” (1870) Peirce treated sets — in other words, the extensions of concepts — as logical aggregates or logical sums. He wrote a plus sign with a comma to indicate an operation of logical addition, abstractly equivalent to inclusive “or”, that was used to form these sums.
to indicate an operation of logical addition, abstractly equivalent to inclusive “or”, that was used to form these sums.
For example, letting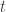 be the concept of the first ten positive integers, it can be expressed as the following logical sum.
be the concept of the first ten positive integers, it can be expressed as the following logical sum.
Relations, as sets of tuples, can also be expressed as logical sums.
For example, letting be the divisibility relation on positive integers, it is possible to think of
be the divisibility relation on positive integers, it is possible to think of  as a logical sum that begins in the following way.
as a logical sum that begins in the following way.
It should be apparent that this is only a form of expression, not a definition, since it takes a prior concept of divisibility to say what ordered pairs appear in the sum, but it’s a reformulation that has its uses, nonetheless.
To be continued …
Define operations on the elementary relatives that obey the following rules:
Extending these rules in the usual distributive fashion to sums of elementary monadic and dyadic relatives allows us to define relative multiplications of the following forms:
For example, expressed in terms of coefficients, the relative product of 2-adic relatives
of 2-adic relatives  and
and 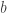 is given by the following formula:
is given by the following formula:
This will of course remind everyone of the formula for multiplying matrices in linear algebra, but I have affixed a comma atop the summation symbol to remind us that the logical sum is the inclusive disjunction — that Peirce wrote as
— that Peirce wrote as  — and not the exclusive disjunction that corresponds to the linear algebraic sum
— and not the exclusive disjunction that corresponds to the linear algebraic sum 
To be continued …
To the extent that mathematics has to do with reasoning about possible existence, or inference from pure hypothesis, a line of thinking going back to Aristotle and developed greatly by C.S. Peirce may have some bearing on the question of How and Why Mathematics is Possible. In that line of thought, hypothesis formation is treated as a case of “abductive” inference, whose job in science generally is to supply suitable raw materials for deduction and induction to develop and test. In that light, a large part of our original question becomes, as Peirce once expressed it —
Is it reasonable to believe that “we can trust to the human mind’s having such a power of guessing right that before very many hypotheses shall have been tried, intelligent guessing may be expected to lead us to the one which will support all tests, leaving the vast majority of possible hypotheses unexamined”? (Peirce, Collected Papers, CP 6.530).
The question may fit the situation in mathematics slightly better if we modify the word hypothesis to say proof.
The Jug of Punch
Bein’ on the twenty-third of June,
As I sat weaving all at my loom,
Bein’ on the twenty-third of June,
As I sat weaving all at my loom,
I heard a thrush, singing on yon bush,
And the song she sang was The Jug of Punch.
What more pleasure can a boy desire,
Than sitting down beside the fire?
What more pleasure can a boy desire,
Than sitting down beside the fire?
And in his hand a jug of punch,
And on his knee a tidy wench.
When I am dead and left in my mould,
At my head and feet place a flowing bowl,
When I am dead and left in my mould,
At my head and feet place a flowing bowl,
And every young man that passes by,
He can have a drink and remember I.
All Liar, No Paradox
According to my understanding of it, the so-called Liar Paradox is just the most simple-minded of fallacies, involving nothing more mysterious than the acceptance of a false assumption, from which anyone can prove anything at all.
Let us contemplate one of the shapes in which the putative Liar Paradox is commonly cast:
Somebody writes down:
1. Statement 1 is false.
Then you are led to reason: If Statement 1 is false then by the principle that permits the substitution of equals in a true statement to obtain yet another true statement, you can derive the result:
“Statement 1 is false” is false. Ergo, Statement 1 is true, and so on, and so on, ad nauseam infinitum.
Where did you go wrong? Where were you misled?
Just here, to wit, where it is writ:
1. Statement 1 is false.
What is this really saying? Well, it’s the same as writing:
Statement 1. Statement 1 is false.
And what the heck does this dot.comment say? It is inducing you to accept this identity:
“Statement 1” = “Statement 1 is false”.
That appears to be a purely syntactic indexing,the sort of thing you are led to believe that you can do arbitrarily, with logical impunity. But you cannot, for syntactic identity implies logical equivalence, and that is liable to find itself constrained by iron bands of logical law.
And you cannot, not with logical impunity, assume the result of this transmutation, which would be as much as to say this:
“Statement 1” = “Negation of Statement 1”
And this my friends, call it “Statement 0”, is purely and simply a false statement, with no hint of paradox about it.
Statement 0 was slipped into your drink before you were even starting to think. A bit before you were led to substitute you should have examined more carefully the site proposed for the substitution!
For the principle that you rushed to use does not permit you to substitute unequals into a statement that is false to begin with, not just in the first place, but even before, in the zeroth place of argument, as it were, and still expect to come up with a truth.
Now let that be the end of that.
Of course, the solution to the conundrum is that statement 1 is sometimes false. If “statement 1 is false” is equivalent to “statement 1 is always false”, then it is an example of where it is false.
For the moment, I am viewing these questions merely as matters of classical propositional logic, even just Boolean formulas.
If we have a Boolean formula like then we do not know whether
then we do not know whether  and
and 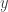 are true or false, but we do know that the formula as a whole is true, because we adopted axioms beforehand to make it so.
are true or false, but we do know that the formula as a whole is true, because we adopted axioms beforehand to make it so.
In that perspective, a form like “1. Statement 1 is true” is just a way of expressing the formula “Statement 1 = (Statement 1 = true)”, which has the form which is true on the adopted axioms.
which is true on the adopted axioms.
FYSMI (funny you should mention it), but I was thinking about Dirac holes just the other day, in connection with an inquiry into Fourier Transforms of Boolean Functions.
I have there a notion of singular propositions, which are Boolean functions that pick out single cells in their given universe of discourse, and I needed a handy name for the complements of these. I suppose I could have been gutsy and called them “Awbrey holes”, but it turns out that a long ago near-namesake of mine is already credited with the discovery of something else entirely under very nearly that name. So I finally settled on crenular propositions.
Someone might enjoy looking at the complexity of Boolean functions as expressed in terms of minimal negation operators. Such expressions have graph-theoretic representations in a species of cactus graphs called painted and rooted cacti, as illustrated here:
• Cactus Language for Propositional Logic
I know I once made a table of more or less canonical cactus expressions for the 256 Boolean functions on 3 variables, but I will have to look for that later.
Peirce’s “Pickwickian” paragraph comes to mind, said Jon Perennially —
— C.S. Peirce, Collected Papers, CP 5.421.
Charles Sanders Peirce, “What Pragmatism Is”, The Monist, Volume 15, 1905, 161–181. Reprinted in the Collected Papers, CP 5.411–437.
— Charles Dickens • Hard Times
One of the first things we learn in systems theory and engineering is that meaningless measures are always the easiest to make and to game. The one thing needful for a meaningful measure is to ask — and to keep on asking — the eminently practical question, “What is the purpose of this system?”
What is the purpose of an educational system? What is the purpose of an economic system? What is the purpose of a governmental system? Take your eyes off those prizes and you lose sight of all.
Benjamin Peirce liked Euler’s Formula so much that he introduced three special symbols for
so much that he introduced three special symbols for  — ones that enable
— ones that enable  to be written in a single cursive ligature, as shown in this note.
to be written in a single cursive ligature, as shown in this note.
… the way our DNA would prove it …
hypotheses non fingerprinto —
But I’m captivated by the fingerprints of finite partial functions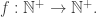
— Geoffrey Chaucer • “The Squire’s Tale”
It sometimes helps to think of a set of boolean functions as a higher order boolean function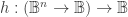 and to view these as a type of generalized quantifiers.
and to view these as a type of generalized quantifiers.
‰
‰ → ‰
Synchronicity Rules❢
I just started reworking an old exposition of mine on Cook’s Theorem, where I borrowed the Parity Function example from Wilf (1986), Algorithms and Complexity, and translated it into the cactus graph syntax for propositional calculus that I developed as an extension of Peirce’s logical graphs.
☞ Parity Machine Example
In the Realm of Riffs and Rotes —
There are pictures of 23 and 512 here.
Re: A Request That We Passed On
Source Copy
A proof predicate has the form and says that
and says that  is a valid proof (in a given formal system) of the formula
is a valid proof (in a given formal system) of the formula 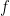 . This is the logical analogue of checking the validity of a computation
. This is the logical analogue of checking the validity of a computation  by a particular machine. A provability predicate then has the form
by a particular machine. A provability predicate then has the form  .
.
The weird fact, which applies to the same natural strong formal systems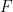 that Kurt Gödel’s famous incompleteness theorems hold for, is that there are statements
that Kurt Gödel’s famous incompleteness theorems hold for, is that there are statements 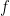 such that
such that 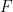 proves
proves 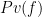 , but does not prove
, but does not prove 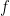 itself.
itself.
Transcription
A proof predicate has the form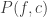 and says that
and says that  is a valid proof (in a given formal system) of the formula
is a valid proof (in a given formal system) of the formula  This is the logical analogue of checking the validity of a computation
This is the logical analogue of checking the validity of a computation  by a particular machine. A provability predicate then has the form
by a particular machine. A provability predicate then has the form 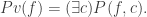
The weird fact, which applies to the same natural strong formal systems that Kurt Gödel’s famous incompleteness theorems hold for, is that there are statements
that Kurt Gödel’s famous incompleteness theorems hold for, is that there are statements  such that
such that  proves
proves 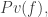 but does not prove
but does not prove  itself.
itself.
Exercise for the Reader —
Draw the Riff and Rote for
— Dante • Purgatorio 09.112–114
— Robert Musil • The Man Without Qualities
Re: “Are there more good cases of isomorphism to study?”
Just off the top of my head, as Data says, there are a couple of examples that come to mind.
Sign Relations. In computational settings, a sign relation is a triadic relation of the form
is a triadic relation of the form  where
where 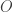 is a set of formal objects under consideration and
is a set of formal objects under consideration and  and
and  are two formal languages used to denote those objects. It is common practice to cut one’s teeth on the special case
are two formal languages used to denote those objects. It is common practice to cut one’s teeth on the special case  before moving on to more solid diets.
before moving on to more solid diets.
Cactus Graphs. In particular, a variant of cactus graphs known (by me, anyway) as painted and rooted cacti (PARCs) affords us with a very efficient graphical syntax for propositional calculus.
I’ll post a few links in the next couple of comments.
Minimal Negation Operators and Painted Cacti
Let
The mathematical objects of penultimate interest are the boolean functions for
for 
A minimal negation operator for
for 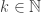 is a boolean function
is a boolean function 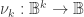 defined as follows:
defined as follows:
•
•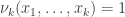 if and only if exactly one of the arguments
if and only if exactly one of the arguments 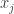 equals
equals 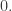
The first few of these operators are already enough to generate all boolean functions via functional composition but the rest of the family is worth keeping around for many practical purposes.
via functional composition but the rest of the family is worth keeping around for many practical purposes.
In most contexts may be written for
may be written for 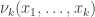 since the number of arguments determines the rank of the operator. In some contexts even the letter
since the number of arguments determines the rank of the operator. In some contexts even the letter  may be omitted, writing just the argument list
may be omitted, writing just the argument list  in which case it helps to use a distinctive typeface for the list delimiters, as
in which case it helps to use a distinctive typeface for the list delimiters, as 
A logical conjunction of arguments can be expressed in terms of minimal negation operators as
arguments can be expressed in terms of minimal negation operators as  and this is conveniently abbreviated as a concatenation of arguments
and this is conveniently abbreviated as a concatenation of arguments 
See the following article for more information:
☞ Minimal Negation Operators
To be continued …
The species of cactus graphs we want here are all constructed from a single family of logical operators called minimal negation operators. The operator
called minimal negation operators. The operator  is a boolean function
is a boolean function 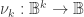 such that
such that 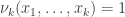 just in case exactly one of the arguments
just in case exactly one of the arguments 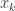 equals
equals 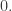
Awbrey, S.M., and Scott, D.K. (August 1993), “Educating Critical Thinkers for a Democratic Society”, in Critical Thinking : The Reform of Education and the New Global Economic Realities, Thirteenth Annual International Conference of The Center for Critical Thinking, Rohnert, CA. ERIC Document ED4703251. Online.
Aristotle understood that the affective is the basis of the cognitive.
☞ Interpretation as Action : The Risk of Inquiry
Let me get some notational matters out of the way before continuing.
I use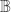 for a generic 2-point set, usually
for a generic 2-point set, usually 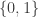 and usually but not always interpreted for logic so that
and usually but not always interpreted for logic so that 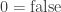 and
and  I use “teletype” parentheses
I use “teletype” parentheses  for negation, so that
for negation, so that 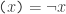 for
for  Later on I’ll be using teletype format lists
Later on I’ll be using teletype format lists  for minimal negation operators.
for minimal negation operators.
As long as we’re reading as a boolean variable
as a boolean variable  the equation
the equation 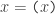 is not paradoxical but simply false. As an algebraic structure
is not paradoxical but simply false. As an algebraic structure 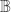 can be extended in many ways but that leaves open the question of whether those extensions have any application to logic.
can be extended in many ways but that leaves open the question of whether those extensions have any application to logic.
On the other hand, the assignment statement makes perfect sense in computational contexts. The effect of the assignment operation on the value of the variable
makes perfect sense in computational contexts. The effect of the assignment operation on the value of the variable  is commonly expressed in time series notation as
is commonly expressed in time series notation as 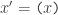 and the same change is expressed even more succinctly by defining
and the same change is expressed even more succinctly by defining  and writing
and writing 
Now suppose we are observing the time evolution of a system with a boolean state variable
with a boolean state variable  and what we observe is the following time series:
and what we observe is the following time series:
Computing the first differences we get:
Computing the second differences we get:
This leads to thinking of the system as having an extended state
as having an extended state 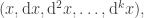 and this additional language gives us the facility of describing state transitions in terms of the various orders of differences. For example, the rule
and this additional language gives us the facility of describing state transitions in terms of the various orders of differences. For example, the rule 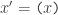 can now be expressed by the rule
can now be expressed by the rule 
The following article has a few more examples along these lines:
☞ Differential Analytic Turing Automata
To my way of thinking, boolean universes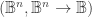 are some of the most fascinating and useful spaces around, so anything that encourages their exploration is a good thing.
are some of the most fascinating and useful spaces around, so anything that encourages their exploration is a good thing.
I doubt if there is any such thing as a perfect calculus or syntactic system for articulating their structure but some are decidedly better than others and any improvement we find makes a positive difference in the order of practical problems we can solve in the time we have at hand.
In that perspective, it seems to me that too fixed a focus on P versus NP leads to a condition of tunnel vision that obstructs the broader exploration of those spaces and the families of calculi for working with them.
Questions about a suitable analogue of differential calculus for boolean spaces keep popping (or pipping) up. Having spent a fair amount of time exploring the most likely analogies between real spaces like and the corresponding boolean spaces
and the corresponding boolean spaces  where
where  I can’t say I’ve gotten all that far, but some of my first few, halting steps are recorded here:
I can’t say I’ve gotten all that far, but some of my first few, halting steps are recorded here:
☞ Differential Logic and Dynamic Systems
We shall not cease from exploration
And the end of all our exploring
Will be to arrive where we started
And know the place for the first time.
— T.S. Eliot • Little Gidding
I can’t remember when I first started playing with Gödel codings of graph-theoretic structures, which arose in logical and computational settings, but I remember being egged on in that direction by Martin Gardner’s 1976 column on Catalan numbers, planted plane trees, polygon dissections, etc.
Codings being injections from a combinatorial species to integers, either non-negative integers
to integers, either non-negative integers 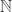 or positive integers
or positive integers 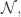 I was especially interested in codings that were also surjective, thereby revealing something about the target domain of arithmetic.
I was especially interested in codings that were also surjective, thereby revealing something about the target domain of arithmetic.
The most interesting bijection I found was between positive integers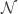 and finite partial functions from
and finite partial functions from 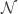 to
to  All of this comes straight out of the primes factorizations. That type of bijection may remind some people of Dana Scott’s
All of this comes straight out of the primes factorizations. That type of bijection may remind some people of Dana Scott’s  Corresponding to the positive integers there arose two species of graphical structures, which I dubbed riffs and rotes.
Corresponding to the positive integers there arose two species of graphical structures, which I dubbed riffs and rotes.
Re: Why Is Congruence Hard To Learn?
I always have pictures like this in my head.
in my head.
I remember having a similar discussion a number of times in the early days of object-oriented programming, or at least when the “fadding crowd” first latched onto it.
We might picture the dyadic relation between Objects and Processes as a rectangular matrix with an entry of indicating where Process
indicating where Process  has meaningful application to Object
has meaningful application to Object 
Then the process orientation amounts to slicing the matrix along columns while the object orientation amounts to slicing it along rows.
But a more general orientation might consider the possibility that the tuples naturally cluster in different ways, partitioning the space into shapes more general than vertical or horizontal stripes.
On Boole’s Ark all cases come two by two. Here’s a sketch of the Case Analysis-Synthesis Theorem (CAST) that weathers any deluge:
Case Analysis-Synthesis Theorem
The most striking example of a “Primitive Insight Proof” (PIP❢) known to me is the Dawes–Utting proof of the Double Negation Theorem from the CSP–GSB axioms for propositional logic. There is a graphically illustrated discussion here. I cannot guess what order of insight it took to find this proof — for me it would have involved a whole lot of random search through the space of possible proofs, and that’s even if I got the notion to look for one.
There is of course a much deeper order of insight into the mathematical form of logical reasoning that it took C.S. Peirce to arrive at his maximally elegant 4-axiom set.
The insight that it takes to find a succinct axiom set for a theoretical domain falls under the heading of abductive or retroductive reasoning, a knack as yet refractory to computational attack, but once we’ve lucked on a select-enough set of axioms we can develop theorems that afford us a more navigable course through the subject.
For example, back on the range of propositional calculus, it takes but a few pivotal theorems and the lever of mathematical induction to derive the Case Analysis-Synthesis Theorem (CAST), which provides a bridge between proof-theoretic methods that demand a modicum of insight and model-theoretic methods that can be run routinely.
“And if we don’t, who puts us away?”
One’s answer, or at least one’s initial response to that question will turn on how one feels about formal realities. As I understand it, reality is that which persists in thumping us on the head until we get what it’s trying to tell us. Are there formal realities, forms that drive us in that way?
Discussions like these tend to begin by supposing we can form a distinction between external and internal. That is a formal hypothesis, not yet born out as a formal reality. Are there formal realities that drive us to recognize them, to pick them out of a crowd of formal possibilities?
Thanks for all that. My snippet was from the B.S. Miller rendering, and I did get an inkling while reading it of an Eleatic influence on the translator. Your recent mention of Arjuna sent me reeling back to some readings and writings I was immersed in 20 years ago. A few days’ digging turned up hard and soft copies of a WinWord mutilation of MacWord document that unfortunately lost all the graphics and half the formatting, but LibreOffice was able to export a MediaWiki text that I could paste up on one of my wikis. Traveling coming up so it may be another couple weeks before I can LaTeX what needs to be LaTeXed, but here is the link for future reference:
☸ Inquiry Driven Systems : Fields Of Inquiry
❤
Skew = Agonic =
Chiaroscuro =
As I read him, Peirce began with a quest to understand how science works, which required him to examine how symbolic mediations inform inquiry, which in turn required him to develop the logic of relatives beyond its bare beginnings in De Morgan. There are therefore intimate links, which I am still trying to understand, among his respective theories of inquiry, signs, and relations.
There’s a bit on the relation between interpretation and inquiry here and a bit more on the three types of inference — abduction, deduction, induction — here.
There is a deep and pervasive analogy between systems of commerce and systems of communication, turning on their near-universal use of symbola (images, media, proxies, signs, symbols, tokens, etc.) to stand for pragmata (objects, objective values, the things we really care about, or would really care about if we examined our values in practice thoroughly enough).
Both types of sign-using systems are prey to the same sort of dysfunction or functional disease — it sets in when their users confuse signs with objects so badly that signs become ends instead of means.
There is a vast literature on this topic, once you think to go looking for it. And it’s a perennial theme in fable and fiction.
☞ Recycling a comment on Cathy O’Neil’s blog from two years ago …
My brother James is a social anthropologist who wrote a dissertation with constant reference to Weber and we used to have long discussions about the routinization of charisma. I came to it from the direction of Meno’s question whether virtue can be taught. So let us add virtuoso, adjective and substantive, to the krater before us.
From what I’ve seen, Peirce’s brand of pragmatism, as an application of the closure cum representation principle known as the pragmatic maxim and incorporating realism about generals, is a sturdier stage for mathematical performance than the derivative styles of neo-pragmatism that Gene Halton aptly described as “fragmatism”.
Immanuel Kant discussed the correspondence theory of truth in the following manner:
Truth is said to consist in the agreement of knowledge with the object. According to this mere verbal definition, then, my knowledge, in order to be true, must agree with the object. Now, I can only compare the object with my knowledge by this means, namely, by taking knowledge of it. My knowledge, then, is to be verified by itself, which is far from being sufficient for truth. For as the object is external to me, and the knowledge is in me, I can only judge whether my knowledge of the object agrees with my knowledge of the object. Such a circle in explanation was called by the ancients Diallelos. And the logicians were accused of this fallacy by the sceptics, who remarked that this account of truth was as if a man before a judicial tribunal should make a statement, and appeal in support of it to a witness whom no one knows, but who defends his own credibility by saying that the man who had called him as a witness is an honourable man. (Kant, 45)
Kant, Immanuel (1800), Introduction to Logic. Reprinted, Thomas Kingsmill Abbott (trans.), Dennis Sweet (intro.), Barnes and Noble, New York, NY, 2005.
There are bits of ambiguity in the use of words like empirical and external.
If by empirical we mean based on experience, then it brings to mind the maxim of a famous intuitionist (whose name I’ve misplaced for the moment, maybe Brouwer?) — There are no non-experienced truths.
When it comes to external, I cannot say how to define that mathematically, but if we replace our criterion of objectitude by independent or universal then those are concepts about which mathematics has definite things to say.
You can still get the old editor by going to:
https://yourblogname.wordpress.com/wp-admin/post-new.php.Réseau
Réseaux
Rousseau
Social compacts come and go
And may converge one day
To one that comes
And never goes
So reap what you réseau
⁂
Manifold • Atlas of Charts
Intersecting circles of competence
Overlapping neighborhoods of expertise
Communities of inquiry as social networks
Some networks are more compact than others
The 12 Latin Squares of Order 3
Re: Did you desire to know this?
To read the writing on the walls, I musta, since I did.
So there must be desires we don’t know we have until we bear their fruits.
Re: Wouldn’t you like to know what’s going on in my mind?
Crazy Old Guy Syndrome
Related discussion at MathBabe
Version 1
As always, it’s a matter of whether our models are adequate to the thing itself, the phenomenon before us.
When it comes to a network that has the capacity to inquire into itself, the way our universe inquires into itself, the main thing lacking in almost all our network models has always been a logical capacity that is adequate to the task.
Version 2
As always, it’s a matter of whether our models are adequate to the thing itself, the phenomenon before us.
If the universe is a network that has the capacity to inquire into itself, the way our universe appears to do through us, then what order of logical capacity is up to that task?
For my part, I don’t think the common run of network models that we are seeing today have enough “logic” in them to do the job. Just to be cute about it, they need more nots in their ether.
Happy Vita Nova❢ You may wish eventually to look into the way that networks, or graphs, can be used to do logic. Doing that requires getting beneath purely positive connections to the varieties of negation that can be used to generate all the rest. Peirce was a pioneer in this pursuit, as evidenced by his logical graphs.
The Alfred E. Neumann Computer &madash;
Maybe it’s a madder of bisociative alge〈bra|s
Less in the way of error-correction and
More in the way of punkreation codes
I used to think about the heap problem a lot when I was programming and I decided the heap quits being a heap as soon as you remove one grain because then it becomes two heaps.
The Pascal sorting of the sorites played on moves between heaps and stacks, but I’ve forgotten the details of that particular epiphany. The whole-system-theoretic point is clear enough though — the system as a whole makes a discrete transition from one state of organization to another.
One classical tradition views logic as a normative science, the one whose object is truth. This puts it on a par with ethics, whose object is justice or morality in action, and aesthetics, whose object is beauty or the admirable in itself.
The pragmatic spin on this line of thinking views logic, ethics, and aesthetics as a concentric series of normative sciences, each a subdiscipline of the next. Logic tells us how we ought to conduct our reasoning in order to achieve the goals of reasoning in general. Thus logic is a special application of ethics. Ethics tells us how we ought to conduct our activities in general in order to achieve the good appropriate to each enterprise. What makes the difference between a normative science and a prescriptive dogma is whether this telling is based on actual inquiry into the relationship of conduct to result, or not.
Here’s a bit more I wrote on this a long time ago in a galaxy not far away —
☞ Logic, Ethics, Aesthetics
Version 2
Making reality our friend is necessary to survival and finding good descriptions of reality is the better part of doing that, so I don’t think we have any less interest in truth than the Ancients. From what I remember, Plato had specific objections to specific styles of art, not to art in general. There is even a Pythagorean tradition that reads The Republic as a metaphorical treatise on music theory, one that serves as a canon for achieving harmony in human affairs. Truth in fiction and myth is a matter of interpretation and — come to think of it — that’s not essentially different from truth in more literal forms of expression.
Version 3
Making reality our friend is necessary to survival and finding good descriptions of reality is the better part of doing that, so I shouldn’t imagine we have any less interest in truth than the Ancients. From what I remember, Plato had specific objections to specific styles of art, not to art in general. There is even a Pythagorean tradition that interprets The Republic as a metaphorical treatise on music theory, no doubt serving incidentally as a canon of harmony in human affairs. Truth in fiction and myth is a matter of interpretation and, come to think of it, that is not essentially different from truth in more literal forms of expression.
These are the forms of time,
which imitates eternity and
revolves according to a law
of number.
Plato • Timaeus • 38 A
Benjamin Jowett (trans.)
It is clear from Aristotle and even Plato in places that the good of reasoning from fair samples and freely chosen examples was bound up with notions of probability, which in the Greek idiom meant likeness, likelihood, and likely stories, in effect, how much the passing image could tell us of the original idea.
Re: Michael Harris • Are Your Colleagues Zombies?
Comment 1
There are many things that could be discussed in this connection, but coming from a perspective informed by Peirce on the nature of inquiry and the whole tradition augured by Freud and Jung on the nature of the unconscious makes for a slightly shifted view of things compared, say, to the pet puzzles of analytic philosophy and rationalistic cognitive psychology.
Comment 2
Let me just ramble a bit and scribble a list of free associative questions that came to mind as I perused your post and sampled a few of its links.
There is almost always in the back of my mind a question about how the species of mathematical inquiry fits within the genus of inquiry in general.
That raises a question about the nature of inquiry. Do machines or zombies — unsouled creatures — inquire or question at all? Is awareness or consciousness necessary to inquiry? Inquiry in general? Mathematical inquiry as a special case?
Comment 3
One of the ideas we get from Peirce is that inquiry begins with the irritation of doubt (IOD) and ends with the fixation of belief (FOB). This fits nicely in the frame of our zombie flick for a couple of reasons: (1) it harks back to Aristotle’s idea that the cognitive is derivative of the affective, (2) it reminds me of what my middle to high school biology texts always enumerated as a defining attribute of living things, their irritability.
Re: John Baez • The Internal Model Principle
Comment 1
Ashby’s book was my own first introduction to cybernetics and I recently returned to his discussion of regulation games in connection with some issues in Peirce’s logic of science or “theory of inquiry”.
In that context it seems like the formula![\rho \subset [\psi^{-1}(G)]\phi](https://s0.wp.com/latex.php?latex=%5Crho+%5Csubset++%5B%5Cpsi%5E%7B-1%7D%28G%29%5D%5Cphi&bg=ffffff&fg=333333&s=0&c=20201002) would have to be saying that the Regulator’s choices are a subset given by applying that portion of the game matrix with goal values in the body to the Disturber’s input.
would have to be saying that the Regulator’s choices are a subset given by applying that portion of the game matrix with goal values in the body to the Disturber’s input.
Comment 2
There’s a far-ranging discussion that could take off from this point — touching on the links among analogical reasoning, arrows and morphisms, cybernetic images, iconic representations, mental models, systems simulations, etc., and just how categorically or not those functions are necessary to intelligent agency, all of which questions have enjoyed large and overlapping literatures for a long time now — but I’m not sure how much of that you meant to open up.
☞ mno
So many modes of mathematical thought,
So many are learned, so few are taught.
There are streams that flow beneath the sea,
There are waves that crash upon the strand,
Lateral thoughts that spread and meander —
Who knows what springs run under the sand?
There are many modes of mathematical thought. The way I see it they all play their part. We have the byways of lateral thinking. We have that “laser-like focus on one topic”. At MathOverFlow they prefer the latter to the exclusion of the lateral. Their logo paints a picture of overflow but they color mostly inside the box.
You May Already Be Subscribed❢
Up till now quantification theory has been based on the assumption of individual variables ranging over universal collections of perfectly determinate elements. Merely to write down quantified formulas like and
and  involves a subscription to such notions, as shown by the membership relations invoked in their indices.
involves a subscription to such notions, as shown by the membership relations invoked in their indices.
The book that struck the deepest chord with me was To Mock a Mockingbird : And Other Logic Puzzles Including an Amazing Adventure in Combinatory Logic, Alfred A. Knopf, New York, NY, 1985.
I once attended a conference at Michigan State on “Creativity in Logic and Math” or some such theme and there was another conference going on down the hall on Birdcalls — seriously — complete with sound effects all afternoon. It made me wonder a little …
At any rate, I found much study there —
☞ Propositions As Types
Contrapositive or modus tollens arguments are very common in mathematics. Since it’s Comedy Hour, I can’t help thinking of Chrysippus, who is said to have died laughing, and his dog — not the one tied to a cart, the one chasing a rabbit or stag or whatever.
Let me resort to a Peircean usage of for
for  and
and 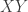 for
for 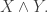
Then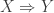 is written
is written 
From a functional point of view it was a step backward when we passed from Peirce’s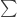 and
and 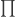 to the present
to the present 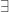 and
and 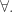 There’s a rough indication of what I mean at the following location:
There’s a rough indication of what I mean at the following location:
☞ Functional Logic : Higher Order Propositions
C.S. Peirce is one who recognized the constitutional independence of mathematical inquiry, finding at its core a mode of operation tantamount to observation and more primitive than logic itself. Here is one place where he expressed that idea.
Normative science rests largely on phenomenology and on mathematics;
metaphysics on phenomenology and on normative science.
— Charles Sanders Peirce, Collected Papers, CP 1.186 (1903)
Syllabus : Classification of Sciences (CP 1.180–202, G-1903-2b)
Re: Gil Kalai • Three Puzzles on Mathematics, Computation, and Games (Part 2 of 3)
Just a tangential association with respect to 2.2.2. I have been exploring questions related to pivotal variables (“Differences that Make a Difference” or “Difference In ⟹ Difference Out”) by means of logical analogues to partial and total differentials.
For example, letting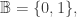 the partial differential operator
the partial differential operator  sends a function
sends a function 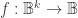 with fiber
with fiber  to a function
to a function 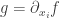 whose fiber
whose fiber  consists of all the places where a change in the value of
consists of all the places where a change in the value of  makes a change in the value of
makes a change in the value of 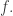
Ref: Differential Logic
If you don’t mind using model-theoretic language, there is for the fact that sentence
for the fact that sentence  is true in model
is true in model 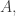 where
where  is defined as a subset of the relevant set
is defined as a subset of the relevant set 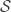 of simple sentences.
of simple sentences.
Cf: My notes on Chang and Keisler (1973) • (4) • (8)
Venn diagrams make for very iconic representations of their universes of discourse. That is one of the main sources of their intuitive utility and also the main source of their logical limitations — they begin to exceed our human capacity for visualization once we climb to 4 or 5 circles (Boolean variables) or so.
Peirce’s logical graphs at the Alpha level (propositional calculus) are somewhat iconic but far less so than Venn diagrams. They are more properly regarded as symbolic representations, in a way that exceeds the logical capacities of icons. That is the source of their considerably greater power as a symbolic calculus.
Here’s a primer on all that:
☞ Logical Graphs • Introduction
C.S. Peirce put forth the idea that what he called “the laws of information” were key to solving “the puzzle of the validity of scientific inference” and thus to understanding the “logic of science”. See my notes on his notorious formula:
Information = Comprehension × Extension
(1 + ⓪ + ① + ② + ③ + ④ + ⑤ + ⑥ + ⑦ + ⑧ + ⑨ + Ⓐ + Ⓑ + Ⓒ + Ⓓ + Ⓔ + Ⓕ)³
Measurement is an extension of perception. Measurement gives us data about an object system the way perception gives us percepts, which we may consider just a species of data.
If we ask when we first became self-conscious about this whole process of perception and measurement, I don’t know, but Aristotle broke ground in a very articulate way with his treatise On Interpretation. Sense data are impressions on the mind and they have their consensual, communicable derivatives in spoken and written signs. This triple interaction among objects, ideas, and signs is the cornerstone of our contemporary theories of signs, commonly known as semiotics.
In many applications a predicate is a function from a universe of discourse to a binary value in
to a binary value in  that is, a characteristic function or indicator function
that is, a characteristic function or indicator function 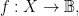 and
and 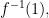 the fiber of
the fiber of  under
under  is the set of elements denoted or indicated by the predicate. That is the semantics, anyway. As far as syntax goes, there are many formal languages whose syntactic expressions serve as names for those functions and nominally speaking one may call those names predicates.
is the set of elements denoted or indicated by the predicate. That is the semantics, anyway. As far as syntax goes, there are many formal languages whose syntactic expressions serve as names for those functions and nominally speaking one may call those names predicates.
Here’s two lines of inquiry I suspect intersect —
☞ http://intersci.ss.uci.edu/wiki/index.php/Differential_Logic_and_Dynamic_Systems_2.0
☞ http://intersci.ss.uci.edu/wiki/index.php/Information_%3D_Comprehension_%C3%97_Extension
Meet you at the corner …
Going back to Aristotle:
Words spoken are symbols or signs (symbola) of affections or impressions (pathemata) of the soul (psyche); written words are the signs of words spoken. As writing, so also is speech not the same for all races of men. But the mental affections themselves, of which these words are primarily signs (semeia), are the same for the whole of mankind, as are also the objects (pragmata) of which those affections are representations or likenesses, images, copies (homoiomata). (Aristotle, De Interp. i. 16a4).
From a Peircean semiotic perspective we can distinguish an object domain and a semiotic plane, so we can have three types of type/token relations: (1) within the object domain, (2) between objects and signs, (3) within the semiotic plane. We could subtilize further but this much is enough for a start.
Type/token relations of type (1) are very common in mathematics and go back to the origins of mathematical thought. These days computer science is rife with them. I’ve seen a lot of confusion about this in Peircean circles as it’s not always grasped that type/token relations are not always all about signs. It can help to speak of types versus instances or instantiations instead.
Aristotle covers type/token relations of types (2) and (3) in De Interp., the latter since he recognizes signs of signs in the clause, “written words are the signs of words spoken”.
I remember a time I was working on a dissertation proposal and having trouble communicating its main points to my advisor. And then it occurred to me that Peirce’s theory of sign relations was the very thing needed to capture the problematics of that communication situation.
I think the underlying issue is whether we want our connectives to be truth-functional or whether we are seeking some sort of “relevance logic”. In the first case the supposed “content” of a proposition, e.g., “Mayo can fly” is irrelevant, only its truth-value enters into the truth-functional conditional. And the truth value of “Mayo can fly” is further irrelevant to the truth of “p ⇒ Mayo can fly” if p is false.
I think the underlying issue is whether we want our connectives to be truth-functional or whether we are seeking some sort of “relevance logic”. In the first case the supposed “content” of a proposition, e.g., is irrelevant, only its truth-value enters into the truth-functional conditional. And the truth value of
is irrelevant, only its truth-value enters into the truth-functional conditional. And the truth value of  is further irrelevant to the truth of
is further irrelevant to the truth of 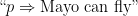 if
if 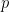 is false.
is false.
These are the forms of time,
which imitates eternity and
revolves according to a law
of number.
Plato • Timaeus • 38 A
Benjamin Jowett (trans.)
The basic idea behind problem reduction goes back to Aristotle’s απαγωγη, variously translated as “abduction”, “reduction”, or “retroduction”, and even earlier to Plato’s question, “Can virtue be taught?” See the following discussion:
🙞 Aristotle’s “Apagogy” • Abductive Reasoning as Problem Reduction
The First Thing About Logic
❝Upon this first, and in one sense this sole, rule of reason, that in order to learn you must desire to learn, and in so desiring not be satisfied with what you already incline to think, there follows one corollary which itself deserves to be inscribed upon every wall of the city of philosophy:
☞ Do not block the way of inquiry ☜
❝Although it is better to be methodical in our investigations, and to consider the economics of research, yet there is no positive sin against logic in trying any theory which may come into our heads, so long as it is adopted in such a sense as to permit the investigation to go on unimpeded and undiscouraged. On the other hand, to set up a philosophy which barricades the road of further advance toward the truth is the one unpardonable offence in reasoning, as it is also the one to which metaphysicians have in all ages shown themselves the most addicted.❞
C.S. Peirce, Collected Papers, CP 1.135–136.
From an unpaginated ms. “F. R. L.”, circa 1899.
http://web.archive.org/web/20061013235600/http://stderr.org/pipermail/inquiry/2004-January/001027.html
Greek nomos
custom, habit, law, manner,
melody, mode or mood (in music),
course of masonry (in architecture)
❝Thus when mothers have children suffering from sleeplessness, and want to lull them to rest, the treatment they apply is to give them, not quiet, but motion, for they rock them constantly in their arms; and instead of silence, they use a kind of crooning noise; and thus they literally cast a spell upon the children (like the victims of a Bacchic frenzy) by employing the combined movements of dance and song as a remedy.❞
❧ Plato • Laws, VII, 790D
☉ ♁ ♃ ☌ ♄ ☺
le stelle ☆ alle stelle ☆ l’amor ♥ che move il sole ☼ e l’altre stelle ☆☆☆
Born in Japan during my Dad and Mom’s tour of occupation duty at the end of WW II and settled back in the Lone Star State when Dad took his Yankee bride and the first 3 of what would come to number 6 kids home. So I grew up in Texas — well, nobody grows up in Texas if you catch my drift — until it was time to head off to college. Had a small scholarship to UT for Fall entry and a larger one to Michigan State but starting Summer. Still planned on heading to Austin but a fight with my Mom — by this time my Dad had been forced to follow the oil to Kuwait and so we saw him but once a year — and the next thing you know I was packing Dad’s old Army footlocker and on the bus North. Texas was still what they now call a Blue State when I left … I do feel partly to blame for what happened after I deprived the State of my moderating influence, but what can a poor boy do? Lived here and there in the Midwest until Reaganomics drove me and my bride South to Galveston and UTMB. University towns are bearable in Texas and Galveston had that distinctive Island culture going for it … but if you wander into the badlands … well, lookout. Better times, barely, brought us back to Mich Again so don’t look for my stone on the Lone Prairie.
It’s funny you should mention Tennyson’s poem in the context of an author’s view of publication as I once laid out a detailed interpretation of the poem as a metaphor on the poet’s quest to communicate. I know I wrote a shorter, sweeter essay on that somewhere I can’t find right now but here’s one of my more turgid dilatations where I used the poem as an “epitext” — a connected series of epigraphs — for a discussion of what I called ostensibly recursive texts (ORTs).
🙞 Inquiry Driven Systems • The Informal Context
“Tennyson’s poem The Lady of Shalott is akin to an ORT, but a bit more remote, since the name styled as ‘The Lady of Shalott’, that the author invokes over the course of the text, is not at first sight the title of a poem, but a title its character adopts and afterwards adapts as the name of a boat. It is only on a deeper reading that this text can be related to or transformed into a proper ORT. Operating on a general principle of interpretation, the reader is entitled to suspect the author is trying to say something about himself, his life, and his work, and that he is likely to be exploiting for this purpose the figure of his ostensible character and the vehicle of his manifest text. If this is an aspect of the author’s intention, whether conscious or unconscious, then the reader has a right to expect several forms of analogy are key to understanding the full intention of the text.”
“Those Who Can Make You Believe Absurdities,
Can Make You Commit Atrocities”
— Voltaire • “Questions sur les Miracles” (1765)
If the People rule, then the People must be wise
It is not a mistake to think people can be educated and informed well enough to rule themselves wisely. But no one should dream that is automatic or easy. But the founders of many a noble experiment in self-rule likely never anticipated the power of modern techno-illogically-amplified mis-education, mis-information, and viral propaganda to create the waking nightmare of every educator — that You Can’t Fix Stupid no matter how hard you try.
Somehow or other I was raised or trained to see crises and problematic situations in general as learning experiences and teachable moments. Later I ran across the following old tag and adopted it as a motto —
🙞 τὰ δὲ μοι παθήματα ἐόντα ἀχάριτα μαθήματα γέγονε
But I recently noticed a strange thing during Facebook exchanges where anyone taking an attitude like that toward the Big Freeze In Texas would find themselves roundly lambasted by a certain sort of person. After some reflection I recognized the pattern and summed it up this way —
Have you noticed the First Rule of Energy Policy —
“Don’t talk about Energy Policy if there’s a current Energy Tragedy”
Imitates the First Rule of Gun Control —
“Don’t talk about Gun Control if there’s a current Tragic Shooting”
Coincidence? I don’t think so …
“It doesn’t matter what one does,” the Man Without Qualities said to himself, shrugging his shoulders. “In a tangle of forces like this it doesn’t make a scrap of difference.” He turned away like a man who has learned renunciation, almost indeed like a sick man who shrinks from any intensity of contact. And then, striding through his adjacent dressing-room, he passed a punching-ball that hung there; he gave it a blow far swifter and harder than is usual in moods of resignation or states of weakness.
❧ Robert Musil • The Man Without Qualities
❝And if he is told that something is the way it is, then he thinks: Well, it could probably just as easily be some other way. So the sense of possibility might be defined outright as the capacity to think how everything could “just as easily” be, and to attach no more importance to what is than to what is not.❞
❧ Robert Musil • The Man Without Qualities
Re: In this post I was less concerned with philosophy than with philology …
Not that I don’t love wisdom and words, however often their stars may cross, but I invoked Musil rather for the way he syzygied the way of the engineer, the way of the mathematician, and the recursive point where their ways diverge. It’s in this frame I think of the word entelechy, which I got from readings in Aristotle, Goethe, and Peirce and promptly gave a personal gloss as end in itself, partly on the influence of Conway’s game theory.
And that’s where I remember all those two-bit pieces I gave up to pinball machines in the early 70s and the critical point in my own trajectory when I realized I would never beat those machines, not that way, not ever, and I turned to the more collaboratory ends of teaching machines how to learn and reason.
♩ On A Related Note ♪ The Music Of The Primes ♫ Riffs & Rotes ♬
Now there’s a progression of progressions I could enjoy, musically speaking, ad infinitum, and yet this pilgrim would consider it progress, mathematically speaking, if he could understand why the sequentiae should be sequenced as they are. Would that understanding add to my enjoyment? On jugera …
Dear Jon,
about riff and rotes, some years ago I create by the prime series, two different series, one starting by 5 and one by 7. All two are structured as rooted tree. All nodes ditance of 6*n (where n is 1,2,3,4,..) by the previous one. Together they create the prime series.
I publish a little example here: https://bertanimauro.github.io/PrimeSeries/ . I don’t know if it can interesting you.
There’s a related discussion with respect to science in general on Thony Christie’s blog —
❧ Both sides of history : Some thoughts on a history of science cliché
I blogged my 2 drachmas’ worth here —
🙞 History, Its Arc, Its Tangents
See Riffs and Rotes for the basic idea.
Here is the Rote for
❝Thus we can understand that “the entire sensible world and all the beings with which we have dealings sometimes appear to us as a text to be deciphered”.❞
❧ Paul Ricoeur • The Conflict of Interpretations
☞ citing Jean Nabert • Elements for an Ethic
🙞 Inquiry Into Inquiry • The Light in the Clearing
Re: Peter Woit • Sabine Hossenfelder
I think Sabine’s point about statistics is instructive. I wish the situation in psychology and the social sciences in general were as halcyon as all that. But the “statistics wars” in that theatre are still ongoing. There’s coverage of the stormier fronts on Deborah Mayo’s blog. I tend to read irreproducible results as a symptom the concepts we are trying to apply are not adequate to the complexity of the thing we are studying, and that’s likely to be the case in many fields.
Also for the daily chatter, if you have time for that sort of thing.
for the daily chatter, if you have time for that sort of thing.
Non‑Breaking Hyphen #8209
Ask for me tomorrow, and you shall find me a grave man.
— Romeo and Juliet • Mercutio 3.1.97–98
Maybe it’s time for a reanimation …