Peirce’s 1870 “Logic of Relatives” • Comment 10.5
We have sufficiently covered the application of the comma functor to absolute terms, so let us return to where we were in working our way through CP 3.73 and see whether we can validate Peirce’s statements about the commafications of dyadic relative terms and the corresponding diagonal extensions to triadic relations.
But not only may any absolute term be thus regarded as a relative term, but any relative term may in the same way be regarded as a relative with one correlate more. It is convenient to take this additional correlate as the first one.
Then
will denote a lover of a woman that is a servant of that woman.
The comma here after should not be considered as altering at all the meaning of
but as only a subjacent sign, serving to alter the arrangement of the correlates.
Just to plant our feet on a more solid stage, let us apply this idea to the Othello example. For this performance only, just to make the example more interesting, let us assume that is secretly in love with
Then we begin with the modified data set:
And next we derive the following results:
Now what are we to make of that?
If we operate in accordance with Peirce’s example of as the “giver of a horse to an owner of that horse” then we may assume the associative and distributive laws remain in force, allowing us to derive the following equation.
Evidently what Peirce means by the associative principle, as it applies to this type of product, is that a product of elementary relatives having the form is equal to
but that no other form of product yields a non-null result. Scanning the implied terms of the triple product tells us that only the case
is non‑null.
It follows that:
And so what Peirce says makes sense in this case.
Resources
cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

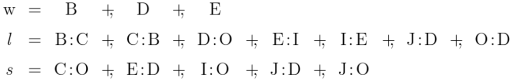
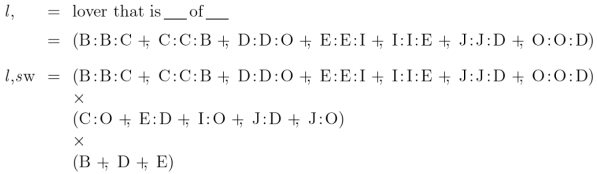
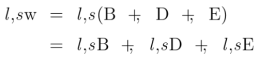

Pingback: Survey of Relation Theory • 3 | Inquiry Into Inquiry
Pingback: Peirce’s 1870 “Logic Of Relatives” • Overview | Inquiry Into Inquiry
Pingback: Peirce’s 1870 “Logic Of Relatives” • Comment 1 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 4 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 5 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 6 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 7 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 8 | Inquiry Into Inquiry