Peirce’s 1870 “Logic of Relatives” • Comment 11.5
Everyone knows the right sort of diagram can be a great aid in rendering complex matters comprehensible. With that in mind, let’s extract what we need from the Relation Theory article to illuminate Peirce’s 1870 Logic of Relatives and use it to fashion what icons we can within the current frame of discussion.
For the immediate present, we may begin with dyadic relations and describe the most frequently encountered species of relations and functions in terms of their local and numerical incidence properties.
Let be an arbitrary dyadic relation. The following properties of
can then be defined.
If is tubular at
then
is known as a partial function or a pre-function from
to
frequently signalized by renaming
with an alternate lower case name, say
and writing
Just by way of formalizing the definition:
To illustrate these properties, let us fashion a generic enough example of a dyadic relation, where
and where the bigraph picture of
is shown in Figure 30.
If we scan along the dimension from
to
we see that the incidence degrees of the
nodes with the
domain are
in that order.
If we scan along the dimension from
to
we see that the incidence degrees of the
nodes with the
domain are
in that order.
Thus, is not total at either
or
since there are nodes in both
and
having incidence degrees less than
Also, is not tubular at either
or
since there are nodes in both
and
having incidence degrees greater than
Clearly then the relation cannot qualify as a pre-function, much less as a function, on either of its relational domains.
Resources
cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)


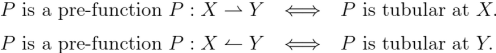

Pingback: Survey of Relation Theory • 3 | Inquiry Into Inquiry
Pingback: Peirce’s 1870 “Logic Of Relatives” • Overview | Inquiry Into Inquiry
Pingback: Peirce’s 1870 “Logic Of Relatives” • Comment 1 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 4 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 5 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 6 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 7 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 8 | Inquiry Into Inquiry