Peirce’s 1870 “Logic of Relatives” • Comment 10.11
Let us return to the point where we left off unpacking the contents of CP 3.73. Here Peirce remarks that the comma operator can be iterated at will.
In point of fact, since a comma may be added in this way to any relative term, it may be added to one of these very relatives formed by a comma, and thus by the addition of two commas an absolute term becomes a relative of two correlates.
So interpreted like
means a man that is a rich individual and is a black [person] that is that rich individual. But this has no other meaning than
or a man that is a black [person] that is rich.
Thus we see that, after one comma is added, the addition of another does not change the meaning at all, so that whatever has one comma after it must be regarded as having an infinite number.
Again, let’s check whether this makes sense on the stage of our small but dramatic model. Let’s say Desdemona and Othello are rich and, among the persons of the play, only they. On this premiss we obtain a sample of absolute terms sufficiently ample to work through Peirce’s example.
One application of the comma operator yields the following dyadic relatives.
Another application of the comma operator generates the following triadic relatives.
Assuming the associativity of multiplication among dyadic relatives, the product may be computed by a brute force method to yield the following result.
This says that a man that is black that is rich is Othello, which is true on the premisses of our present universe of discourse.
Following the standard associative combinations of the product
is multiplied out along the following lines, where the trinomials of the form
are the only ones producing a non‑null result, namely,
So we have that
In closing, observe how the teridentity relation has turned up again in this context, as the second comma‑ing of the universal term itself.
Resources
cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)


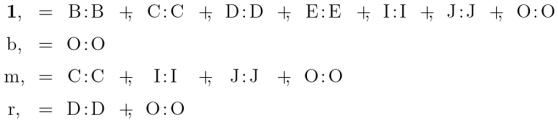
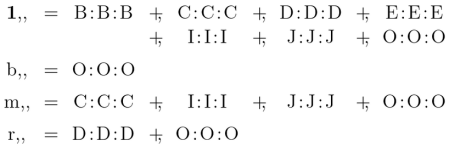

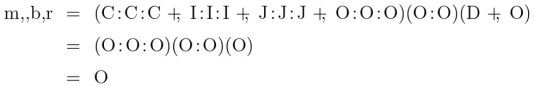

Pingback: Survey of Relation Theory • 3 | Inquiry Into Inquiry
Pingback: Peirce’s 1870 “Logic Of Relatives” • Overview | Inquiry Into Inquiry
Pingback: Peirce’s 1870 “Logic Of Relatives” • Comment 1 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 4 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 5 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 6 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 7 | Inquiry Into Inquiry
Pingback: Survey of Relation Theory • 8 | Inquiry Into Inquiry