A Curious Truth of Classical Logic
Peirce’s law is a propositional calculus formula which states a non‑obvious truth of classical logic and affords a novel way of defining classical propositional calculus.
Introduction
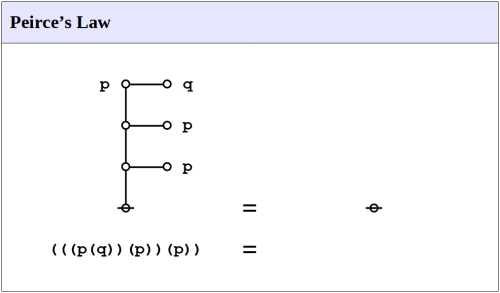
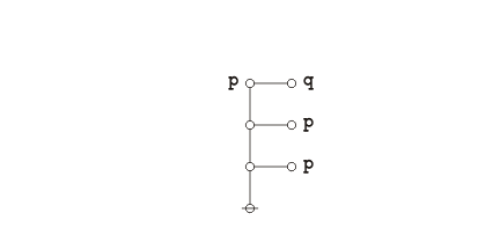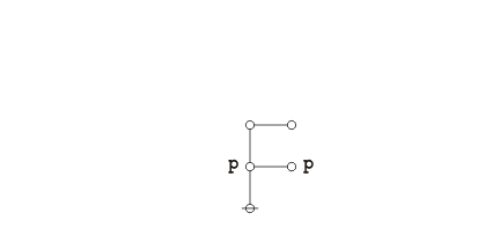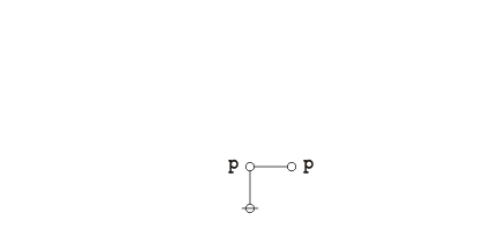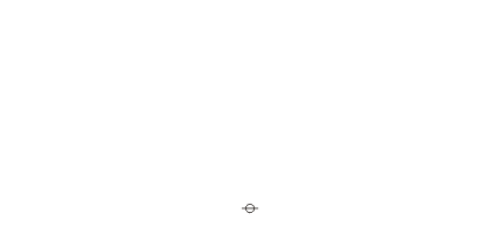
Peirce’s law is commonly expressed in the following form.
Peirce’s law holds in classical propositional calculus, but not in intuitionistic propositional calculus. The precise axiom system one chooses for classical propositional calculus determines whether Peirce’s law is taken as an axiom or proven as a theorem.
History
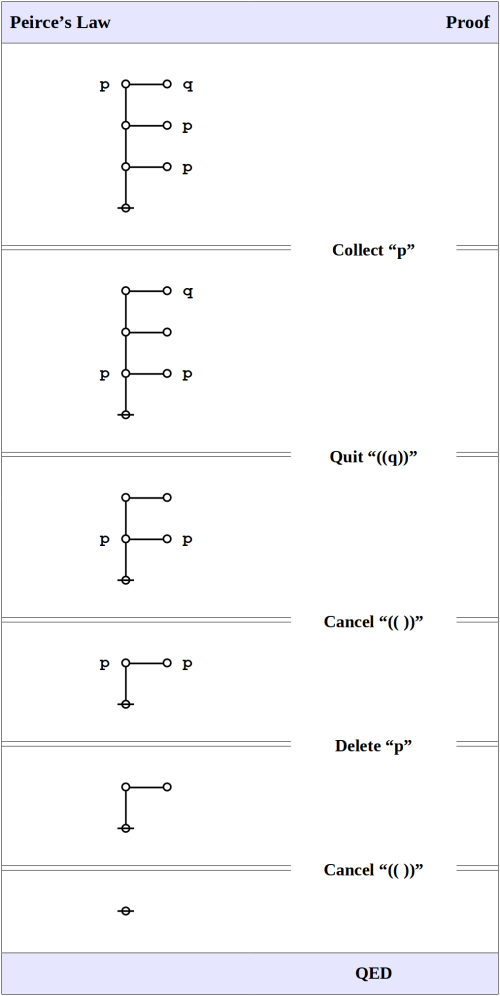
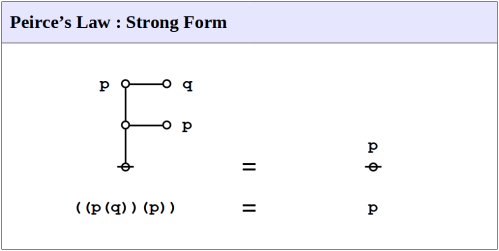
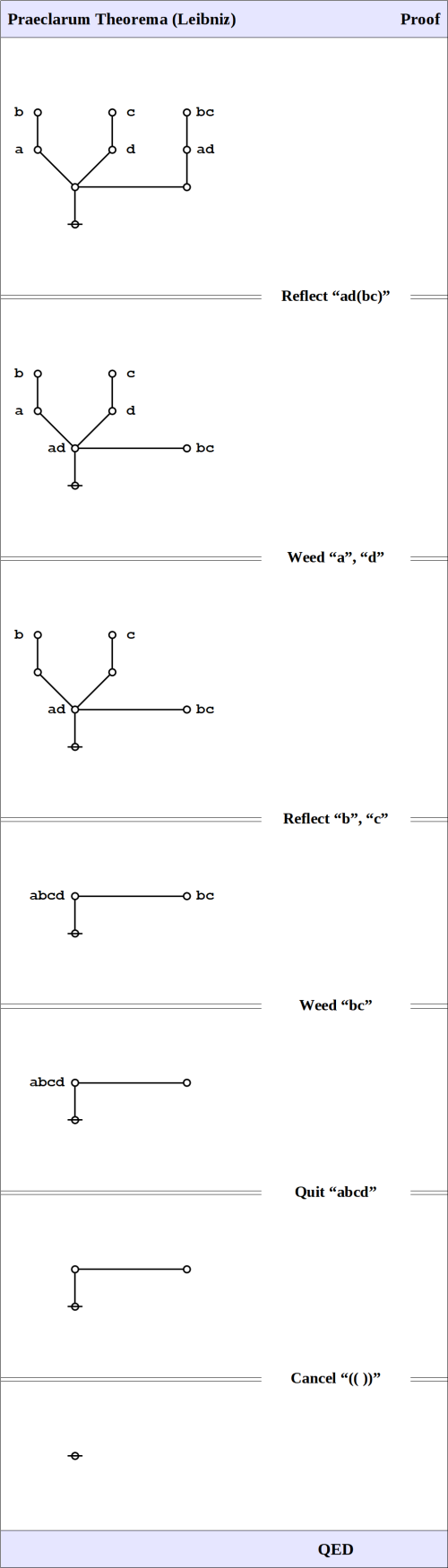
Here is Peirce’s own statement and proof of the law:
A fifth icon is required for the principle of excluded middle and other propositions connected with it. One of the simplest formulae of this kind is:
This is hardly axiomatical. That it is true appears as follows. It can only be false by the final consequent being false while its antecedent
is true. If this is true, either its consequent,
is true, when the whole formula would be true, or its antecedent
is false. But in the last case the antecedent of
that is
must be true. (Peirce, CP 3.384).
Peirce goes on to point out an immediate application of the law:
From the formula just given, we at once get:
where the is used in such a sense that
means that from
every proposition follows. With that understanding, the formula states the principle of excluded middle, that from the falsity of the denial of
follows the truth of
(Peirce, CP 3.384).
Note. Peirce uses the sign of illation for implication. In one place he explains
as a variant of the sign
for less than or equal to; in another place he suggests that
is an iconic way of representing a state of affairs where
in every way that it can be, is
References
- Peirce, Charles Sanders (1885), “On the Algebra of Logic : A Contribution to the Philosophy of Notation”, American Journal of Mathematics 7 (1885), 180–202. Reprinted (CP 3.359–403), (CE 5, 162–190).
- Peirce, Charles Sanders (1931–1935, 1958), Collected Papers of Charles Sanders Peirce, vols. 1–6, Charles Hartshorne and Paul Weiss (eds.), vols. 7–8, Arthur W. Burks (ed.), Harvard University Press, Cambridge, MA. Cited as (CP volume.paragraph).
- Peirce, Charles Sanders (1981–), Writings of Charles S. Peirce : A Chronological Edition, Peirce Edition Project (eds.), Indiana University Press, Bloomington and Indianapolis, IN. Cited as (CE volume, page).
Resources
- Logic Syllabus • Logical Graphs • Peirce’s Law
- Metamath Proof Explorer • Peirce’s Axiom
- Charles Sanders Peirce • Bibliography
cc: FB | Logical Graphs • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science