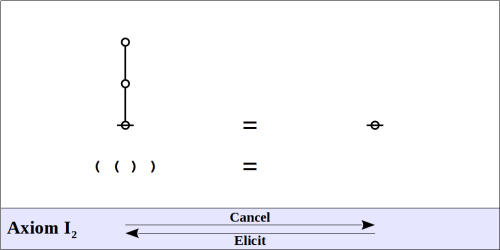
The formal system of logical graphs is defined by a foursome of formal equations, called initials when regarded purely formally, in abstraction from potential interpretations, and called axioms when interpreted as logical equivalences.  There are two arithmetic initials and two algebraic initials, as shown below.

Arithmetic Initials

Algebraic Initials

Spencer Brown uses a different formal equation for his first algebraic initial — where I use    he uses    For the moment, let’s refer to my as and his as and use that notation to examine the relationship between the two systems.

It is easy to see that the two systems are equivalent, since we have the following proof of by way of and

 a   a
 o---o
 |
 @

 =======J1a {delete}

 o---o
 |
 @

 =======I2  {cancel}

 @

 =======QED J1b

In choosing between systems I am less concerned with small differences in the lengths of proofs than I am with other factors.  It is difficult for me to remember all the reasons for decisions I made forty or fifty years ago — as a general rule, Peirce’s way of looking at the relation between mathematics and logic has long been a big influence on my thinking and the other main impact is accountable to the nuts and bolts requirements of computational representation.

But looking at the choice with present eyes, I think I continue to prefer the system over the alternative simply for the fact it treats two different types of operation separately, namely, changes in graphical structure versus changes in the placement of variables.

cc: Cybernetics • Laws of Form • Ontolog • Peirce • Structural Modeling • Systems Science