Re: Genus, Species, Pie Charts, Radio Buttons • 1
Re: Laws of Form • William Bricken

A problem we often encounter is the need to relate a variety of formal languages to the same domain of formal objects.  In our present engagement we are using languages not only to describe but further to compute with the objects in question and so we call our languages so many diverse calculi.

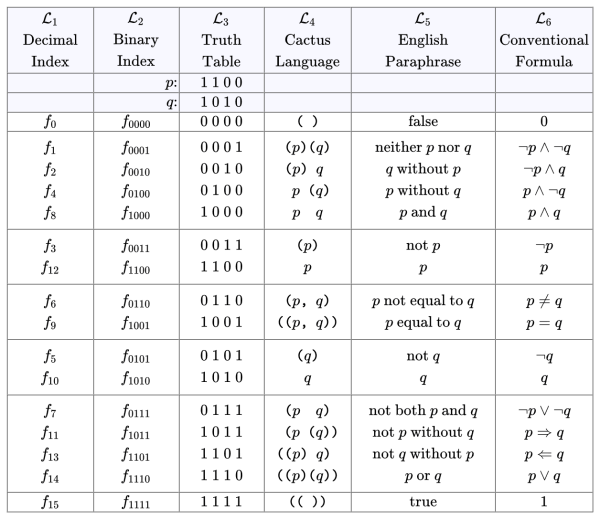
When it comes to propositional calculi, a couple of Tables may be useful at this point and also for future reference.  They present two arrangements of the sixteen boolean functions on two variables, collating their truth tables with their expressions in several systems of notation, including the parenthetical versions of cactus expressions, here read under the existential interpretation.  They appear as the first two Tables on the following page.

Differential Logic and Dynamic Systems • Appendices

The copies I posted to my blog will probably load faster.

Differential Logic • 8

Table A1.  Propositional Forms on Two Variables • Index Order

Differential Logic • 9

Table A2.  Propositional Forms on Two Variables • Orbit Order

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Minimal Negation Operators • Laws of Form • Peirce List (1) (2) (3)