Inquiry Into Inquiry

§1.  Three Kinds Of Signs (concl.)

In this paper, I purpose to develop an algebra adequate to the treatment of all problems of deductive logic, showing as I proceed what kinds of signs have necessarily to be employed at each stage of the development.  I shall thus attain three objects.  The first is the extension of the power of logical algebra over the whole of its proper realm.  The second is the illustration of principles which underlie all algebraic notation.  The third is the enumeration of the essentially different kinds of necessary inference;  for when the notation which suffices for exhibiting one inference is found inadequate for explaining another, it is clear that the latter involves an inferential element not present to the former.  Accordingly, the procedure contemplated should result in a list of categories of reasoning, the interest of which is not dependent upon the algebraic way of considering the subject.

I shall not be able to perfect the algebra sufficiently to give facile methods of reaching logical conclusions:  I can only give a method by which any legitimate conclusion may be reached and any fallacious one avoided.  But I cannot doubt that others, if they will take up the subject, will succeed in giving the notation a form in which it will be highly useful in mathematical work.  I even hope that what I have done may prove a first step toward the resolution of one of the main problems of logic, that of producing a method for the discovery of methods in mathematics.  (3.364).

§1.  Three Kinds Of Signs (cont.)

For instance, take the syllogistic formula,

This is really a diagram of the relations of and   The fact that the middle term occurs in the two premisses is actually exhibited, and this must be done or the notation will be of no value.

As for algebra, the very idea of the art is that it presents formulæ which can be manipulated, and that by observing the effects of such manipulation we find properties not to be otherwise discerned.  In such manipulation, we are guided by previous discoveries which are embodied in general formulæ.  These are patterns which we have the right to imitate in our procedure, and are the icons par excellence of algebra.  The letters of applied algebra are usually tokens, but the etc. of a general formula, such as

are blanks to be filled up with tokens, they are indices of tokens.  Such a formula might, it is true, be replaced by an abstractly stated rule (say that multiplication is distributive);  but no application could be made of such an abstract statement without translating it into a sensible image.  (3.363).

§1.  Three Kinds Of Signs (cont.)

I have taken pains to make my distinction of icons, indices, and tokens clear, in order to enunciate this proposition:  in a perfect system of logical notation signs of these several kinds must all be employed.  Without tokens there would be no generality in the statements, for they are the only general signs;  and generality is essential to reasoning.  Take, for example, the circles by which Euler represents the relations of terms.  They well fulfill the function of icons, but their want of generality and their incompetence to express propositions must have been felt by everybody who has used them.  Mr. Venn has, therefore, been led to add shading to them;  and this shading is a conventional sign of the nature of a token.  In algebra, the letters, both quantitative and functional, are of this nature.

But tokens alone do not state what is the subject of discourse;  and this can, in fact, not be described in general terms;  it can only be indicated.  The actual world cannot be distinguished from a world of imagination by any description.  Hence the need of pronouns and indices, and the more complicated the subject the greater the need of them.  The introduction of indices into the algebra of logic is the greatest merit of Mr. Mitchell’s system.  He writes to mean that the proposition is true of every object in the universe, and to mean that the same is true of some object.  This distinction can only be made in some such way as this.  Indices are also required to show in what manner other signs are connected together.

With these two kinds of signs alone any proposition can be expressed;  but it cannot be reasoned upon, for reasoning consists in the observation that where certain relations subsist certain others are found, and it accordingly requires the exhibition of the relations reasoned with in an icon.  It has long been a puzzle how it could be that, on the one hand, mathematics is purely deductive in its nature, and draws its conclusions apodictically, while on the other hand, it presents as rich and apparently unending a series of surprising discoveries as any observational science.  Various have been the attempts to solve the paradox by breaking down one or other of these assertions, but without success.  The truth, however, appears to be that all deductive reasoning, even simple syllogism, involves an element of observation;  namely, deduction consists in constructing an icon or diagram the relations of whose parts shall present a complete analogy with those of the parts of the object of reasoning, of experimenting upon this image in the imagination, and of observing the result so as to discover unnoticed and hidden relations among the parts.  (3.363).

§1.  Three Kinds Of Signs

Any character or proposition either concerns one subject, two subjects, or a plurality of subjects.  For example, one particle has mass, two particles attract one another, a particle revolves about the line joining two others.  A fact concerning two subjects is a dual character or relation;  but a relation which is a mere combination of two independent facts concerning the two subjects may be called degenerate, just as two lines are called a degenerate conic.  In like manner a plural character or conjoint relation is to be called degenerate if it is a mere compound of dual characters.  (3.359).

A sign is in a conjoint relation to the thing denoted and to the mind.  If this triple relation is not of a degenerate species, the sign is related to its object only in consequence of a mental association, and depends upon a habit.  Such signs are always abstract and general, because habits are general rules to which the organism has become subjected.  They are, for the most part, conventional or arbitrary.  They include all general words, the main body of speech, and any mode of conveying a judgment.  For the sake of brevity I will call them tokens.  [Note. Peirce more frequently calls these symbols.]  (3.360).

But if the triple relation between the sign, its object, and the mind, is degenerate, then of the three pairs

two at least are in dual relations which constitute the triple relation.  One of the connected pairs must consist of the sign and its object, for if the sign were not related to its object except by the mind thinking of them separately, it would not fulfill the function of a sign at all.  Supposing, then, the relation of the sign to its object does not lie in a mental association, there must be a direct dual relation of the sign to its object independent of the mind using the sign.  In the second of the three cases just spoken of, this dual relation is not degenerate, and the sign signifies its object solely by virtue of being really connected with it.  Of this nature are all natural signs and physical symptoms.  I call such a sign an index, a pointing finger being the type of this class.

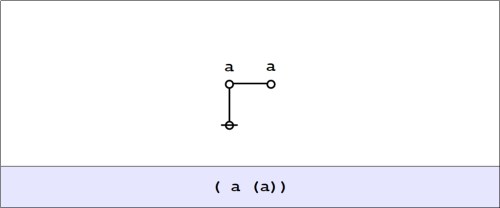
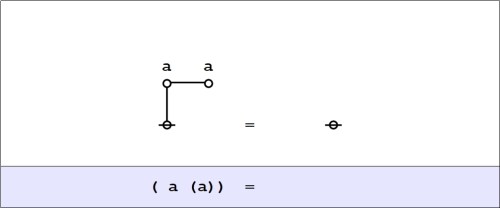
The index asserts nothing;  it only says “There!”  It takes hold of our eyes, as it were, and forcibly directs them to a particular object, and there it stops.  Demonstrative and relative pronouns are nearly pure indices, because they denote things without describing them;  so are the letters on a geometrical diagram, and the subscript numbers which in algebra distinguish one value from another without saying what those values are.  (3.361).

The third case is where the dual relation between the sign and its object is degenerate and consists in a mere resemblance between them.  I call a sign which stands for something merely because it resembles it, an icon.  Icons are so completely substituted for their objects as hardly to be distinguished from them.  Such are the diagrams of geometry.  A diagram, indeed, so far as it has a general signification, is not a pure icon;  but in the middle part of our reasonings we forget that abstractness in great measure, and the diagram is for us the very thing.  So in contemplating a painting, there is a moment when we lose consciousness that it is not the thing, the distinction of the real and the copy disappears, and it is for the moment a pure dream — not any particular existence, and yet not general.  At that moment we are contemplating an icon.  (3.362).