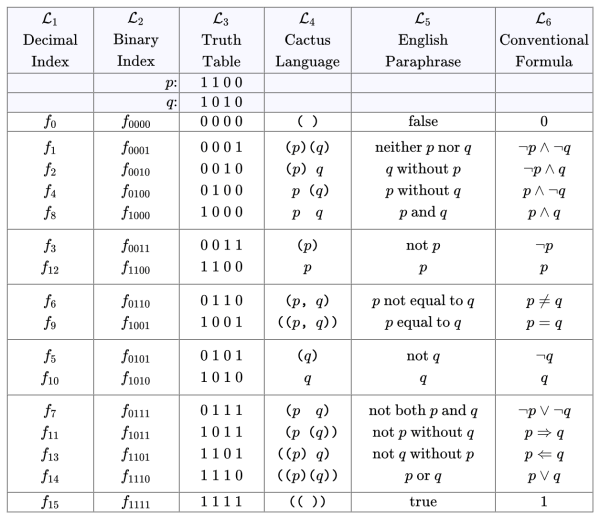
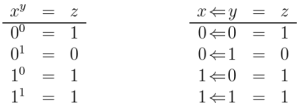In this Survey of blog and wiki posts on Relation Theory, relations are viewed from the perspective of combinatorics, in other words, as a topic in discrete mathematics, with special attention to finite structures and concrete set-theoretic constructions, many of which arise quite naturally in applications. This approach to relation theory is distinct from, though closely related to, its study from the perspectives of abstract algebra on the one hand and formal logic on the other.
Elements
Relational Concepts
| Relation Construction | Relation Composition | Relation Reduction |
| Relative Term | Sign Relation | Triadic Relation |
| Logic of Relatives | Hypostatic Abstraction | Continuous Predicate |
Illustrations
Blog Series
Peirce’s 1870 “Logic of Relatives”
- Overview
- Preliminaries
- Selection 1 • Use of the Letters
- Selection 2 • Numbers Corresponding to Letters
- Selection 3 • The Signs of Inclusion, Equality, Etc.
- Selection 4 • The Signs for Addition
- Selection 5 • The Signs for Multiplication
- Selection 6 • The Signs for Multiplication (cont.)
- Comment 6.1 • Sets as Sums
- Selection 7 • The Signs for Multiplication (cont.)
- Comment 7.1 • Proto-Graphical Syntax
- Selection 8 • The Signs for Multiplication (cont.)
- Selection 9 • The Signs for Multiplication (cont.)
- Selection 10 • The Signs for Multiplication (cont.)
- Selection 11 • The Signs for Multiplication (concl.)
- Comment 11.1
- Comment 11.2
- Comment 11.3
- Comment 11.4
- Comment 11.5
- Comment 11.6
- Comment 11.7
- Comment 11.8
- Comment 11.9
- Comment 11.10
- Comment 11.11
- Comment 11.12
- Comment 11.13
- Comment 11.14
- Comment 11.15
- Comment 11.16
- Comment 11.17
- Comment 11.18
- Comment 11.19
- Comment 11.20
- Comment 11.21
- Comment 11.22
- Comment 11.23
- Comment 11.24
- Selection 12 • The Sign of Involution
- Intermezzo
Peirce’s 1880 “Algebra of Logic” Chapter 3
- Preliminaries
- Selections • (1) • (2) • (3) • (4) • (5) • (6) • (7) • (8)
- Comments • (7.1) • (7.2) • (7.3) • (7.4) • (7.5)