Casual Introduction (cont.)

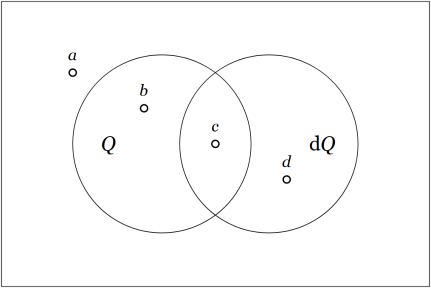
Figure 3 returns to the situation in Figure 1, but this time interpolates a new quality specifically tailored to account for the relation between Figure 1 and Figure 2.

This new quality, is an example of a differential quality, since its absence or presence qualifies the absence or presence of change occurring in another quality.  As with any other quality, it is represented in the venn diagram by means of a “circle” distinguishing two halves of the universe of discourse, in this case, the portions of outside and inside the region

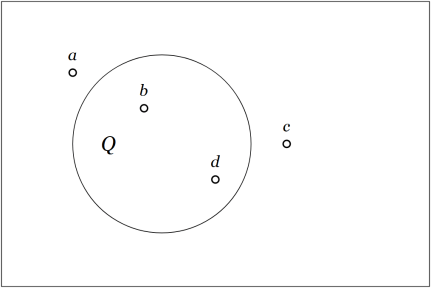
Figure 1 represents a universe of discourse, together with a basis of discussion, for expressing propositions about the contents of that universe.  Once the quality is given a name, say, the symbol we have the basis for a formal language specifically cut out for discussing in terms of   This language is more formally known as the propositional calculus with alphabet

In the context marked by and there are just four distinct pieces of information which can be expressed in the corresponding propositional calculus, namely, the constant proposition the negative proposition the positive proposition and the constant proposition

For example, referring to the points in Figure 1, the constant proposition holds of no points, the negative proposition holds of and the positive proposition holds of and and the constant proposition holds of all points in the sample.

Figure 3 preserves the same universe of discourse and extends the basis of discussion to a set of two qualities,   In corresponding fashion, the initial propositional calculus is extended by means of the enlarged alphabet,

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Casual Introduction (cont.)

Now consider the situation represented by the venn diagram in Figure 2.

Figure 2 differs from Figure 1 solely in the circumstance that the object is outside the region while the object is inside the region   So far, nothing says our encountering these Figures in this order is other than purely accidental but if we interpret this sequence of frames as a “moving picture” representation of their natural order in a temporal process then it would be natural to suppose and have remained as they were with regard to the quality while and have changed their standings in that respect.  In particular, has moved from the region where is true to the region where is false while has moved from the region where is false to the region where is true.

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

A differential propositional calculus is a propositional calculus extended by a set of terms for describing aspects of change and difference, for example, processes taking place in a universe of discourse or transformations mapping a source universe to a target universe.

Casual Introduction

Consider the situation represented by the venn diagram in Figure 1.

The area of the rectangle represents a universe of discourse,   The universe under discussion may be a population of individuals having various additional properties or it may be a collection of locations occupied by various individuals.  The area of the “circle” represents the individuals having the property or the locations in the corresponding region   Four individuals, are singled out by name.  It happens that and currently reside in region while and do not.

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Here’s the outline of a sketch I wrote on differential propositional calculi, which extend propositional calculi by adding terms for describing aspects of change and difference, for example, processes taking place in a universe of discourse or transformations mapping a source universe to a target universe.  I wrote this as an intuitive introduction to differential logic, which is my best effort so far at dealing with the ancient and persistent problems of treating diversity and mutability in logical terms.  I’ll be looking at ways to improve this draft as I serialize it to my blog.

Part 1

Casual Introduction

Cactus Calculus

Part 2

Formal_Development

Elementary Notions

Special Classes of Propositions

Linear Propositions

Positive Propositions

Singular Propositions

Differential Extensions

Appendices

Appendices

Appendix 1. Propositional Forms and Differential Expansions

Table A1. Propositional Forms on Two Variables

Table A2. Propositional Forms on Two Variables

Table A3. Ef Expanded Over Differential Features

Table A4. Df Expanded Over Differential Features

Table A5. Ef Expanded Over Ordinary Features

Table A6. Df Expanded Over Ordinary Features

Appendix 2. Differential Forms

Table A7. Differential Forms Expanded on a Logical Basis

Table A8. Differential Forms Expanded on an Algebraic Basis

Table A9. Tangent Proposition as Pointwise Linear Approximation

Table A10. Taylor Series Expansion Df = df + d²f

Table A11. Partial Differentials and Relative Differentials

Table A12. Detail of Calculation for the Difference Map

Appendix 3. Computational Details

Operator Maps for the Logical Conjunction f₈(u, v)

Computation of εf₈

Computation of Ef₈

Computation of Df₈

Computation of df₈

Computation of rf₈

Computation Summary for Conjunction

Operator Maps for the Logical Equality f₉(u, v)

Computation of εf₉

Computation of Ef₉

Computation of Df₉

Computation of df₉

Computation of rf₉

Computation Summary for Equality

Operator Maps for the Logical Implication f₁₁(u, v)

Computation of εf₁₁

Computation of Ef₁₁

Computation of Df₁₁

Computation of df₁₁

Computation of rf₁₁

Computation Summary for Implication

Operator Maps for the Logical Disjunction f₁₄(u, v)

Computation of εf₁₄

Computation of Ef₁₄

Computation of Df₁₄

Computation of df₁₄

Computation of rf₁₄

Computation Summary for Disjunction

Appendix 4. Source Materials

Appendix 5. Various Definitions of the Tangent Vector

References

References

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science