Formal Development (cont.)

Before moving on, let’s unpack some of the assumptions, conventions, and implications involved in the array of concepts and notations introduced above.

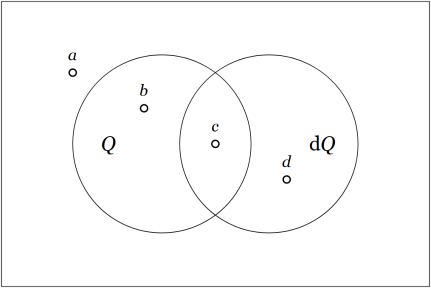
A universe of discourse qualified by the logical features is a set plus the set of all functions from the space to the boolean domain   There are elements in often pictured as the cells of a venn diagram or the nodes of a hypercube.  There are possible functions from to accordingly pictured as all the ways of painting the cells of a venn diagram or the nodes of a hypercube with a palette of two colors.

A logical proposition about the elements of is either true or false of each element in while a function evaluates to or on each element of   The analogy between logical propositions and boolean-valued functions is close enough to adopt the latter as models of the former and simply refer to the functions as propositions about the elements of

Resources

• Logic Syllabus
• Differential Logic and Dynamic Systems
• Functional Conception of Propositional Calculus
• Qualitative Logic and Quantitative Analogy
• Formal Terms and Flexible Types

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Formal Development

The preceding discussion outlined the ideas leading to the differential extension of propositional logic.  The next task is to lay out the concepts and terminology needed to describe various orders of differential propositional calculi.

Elementary Notions

Logical description of a universe of discourse begins with a collection of logical signs.  For simplicity in a first approach we assume the signs are collected in the form of a finite alphabet,   The signs are interpreted as denoting logical features, for example, properties of objects in the universe of discourse or simple propositions about those objects.  Corresponding to the alphabet there is then a set of logical features,

A set of logical features affords a basis for generating an -dimensional universe of discourse, written   It is useful to consider a universe of discourse as a categorical object incorporating both the set of points and the set of propositions implicit with the ordinary picture of a venn diagram on features.  Accordingly, the universe of discourse may be regarded as an ordered pair having the type and this last type designation may be abbreviated as or even more succinctly as   For convenience, the data type of a finite set on elements may be indicated by either one of the equivalent notations, or

Table 7 summarizes the notations needed to describe ordinary propositional calculi in a systematic fashion.

Resources

• Logic Syllabus
• Differential Logic and Dynamic Systems
• Functional Conception of Propositional Calculus

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Cactus Calculus

Table 6 outlines a syntax for propositional calculus based on two types of logical connectives, both of variable -ary scope.

• A bracketed sequence of propositional expressions is taken to mean exactly one of the propositions is false, in other words, their minimal negation is true.
• A concatenated sequence of propositional expressions is taken to mean every one of the propositions is true, in other words, their logical conjunction is true.

All other propositional connectives can be obtained through combinations of the above two forms.  Strictly speaking, the concatenation form is dispensable in light of the bracket form, but it is convenient to maintain it as an abbreviation for more complicated bracket expressions.  While working with expressions solely in propositional calculus, it is easiest to use plain parentheses for logical connectives.  In contexts where parentheses are needed for other purposes “teletype” parentheses or barred parentheses may be used for logical operators.

The briefest expression for logical truth is the empty word, abstractly denoted or in formal languages, where it forms the identity element for concatenation.  It may be given visible expression in this context by means of the logically equivalent form or, especially if operating in an algebraic context, by a simple   Also when working in an algebraic mode, the plus sign may be used for exclusive disjunction.  For example, we have the following paraphrases of algebraic expressions:

It is important to note the last expressions are not equivalent to the triple bracket

More information about this syntax for propositional calculus can be found at the following locations.

Resources

• Logic Syllabus
• Zeroth Order Logic
• Minimal Negation Operators

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Casual Introduction (concl.)

Table 5 shows the rules of inference responsible for giving the differential quality its meaning in practice.

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Casual Introduction (cont.)

Figure 3 extends the basis of description for the space to a set of two qualities and the corresponding terms of description to an alphabet of two symbols

Any propositional calculus over two basic propositions allows for the expression of sixteen propositions all together.  Salient among those propositions in the present setting are the four which single out the individual sample points at the initial moment of observation.  Table 4 lists the initial state descriptions, using overlines to express logical negations.

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Casual Introduction (cont.)

Figure 3 returns to the situation in Figure 1, but this time interpolates a new quality specifically tailored to account for the relation between Figure 1 and Figure 2.

This new quality, is an example of a differential quality, since its absence or presence qualifies the absence or presence of change occurring in another quality.  As with any other quality, it is represented in the venn diagram by means of a “circle” distinguishing two halves of the universe of discourse, in this case, the portions of outside and inside the region

Figure 1 represents a universe of discourse, together with a basis of discussion, for expressing propositions about the contents of that universe.  Once the quality is given a name, say, the symbol we have the basis for a formal language specifically cut out for discussing in terms of   This language is more formally known as the propositional calculus with alphabet

In the context marked by and there are just four distinct pieces of information which can be expressed in the corresponding propositional calculus, namely, the constant proposition the negative proposition the positive proposition and the constant proposition

For example, referring to the points in Figure 1, the constant proposition holds of no points, the negative proposition holds of and the positive proposition holds of and and the constant proposition holds of all points in the sample.

Figure 3 preserves the same universe of discourse and extends the basis of discussion to a set of two qualities,   In corresponding fashion, the initial propositional calculus is extended by means of the enlarged alphabet,

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Casual Introduction (cont.)

Now consider the situation represented by the venn diagram in Figure 2.

Figure 2 differs from Figure 1 solely in the circumstance that the object is outside the region while the object is inside the region   So far, nothing says our encountering these Figures in this order is other than purely accidental but if we interpret this sequence of frames as a “moving picture” representation of their natural order in a temporal process then it would be natural to suppose and have remained as they were with regard to the quality while and have changed their standings in that respect.  In particular, has moved from the region where is true to the region where is false while has moved from the region where is false to the region where is true.

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

A differential propositional calculus is a propositional calculus extended by a set of terms for describing aspects of change and difference, for example, processes taking place in a universe of discourse or transformations mapping a source universe to a target universe.

Casual Introduction

Consider the situation represented by the venn diagram in Figure 1.

The area of the rectangle represents a universe of discourse,   The universe under discussion may be a population of individuals having various additional properties or it may be a collection of locations occupied by various individuals.  The area of the “circle” represents the individuals having the property or the locations in the corresponding region   Four individuals, are singled out by name.  It happens that and currently reside in region while and do not.

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Here’s the outline of a sketch I wrote on differential propositional calculi, which extend propositional calculi by adding terms for describing aspects of change and difference, for example, processes taking place in a universe of discourse or transformations mapping a source universe to a target universe.  I wrote this as an intuitive introduction to differential logic, which is my best effort so far at dealing with the ancient and persistent problems of treating diversity and mutability in logical terms.  I’ll be looking at ways to improve this draft as I serialize it to my blog.

Part 1

Casual Introduction

Cactus Calculus

Part 2

Formal_Development

Elementary Notions

Special Classes of Propositions

Linear Propositions

Positive Propositions

Singular Propositions

Differential Extensions

Appendices

Appendices

Appendix 1. Propositional Forms and Differential Expansions

Table A1. Propositional Forms on Two Variables

Table A2. Propositional Forms on Two Variables

Table A3. Ef Expanded Over Differential Features

Table A4. Df Expanded Over Differential Features

Table A5. Ef Expanded Over Ordinary Features

Table A6. Df Expanded Over Ordinary Features

Appendix 2. Differential Forms

Table A7. Differential Forms Expanded on a Logical Basis

Table A8. Differential Forms Expanded on an Algebraic Basis

Table A9. Tangent Proposition as Pointwise Linear Approximation

Table A10. Taylor Series Expansion Df = df + d²f

Table A11. Partial Differentials and Relative Differentials

Table A12. Detail of Calculation for the Difference Map

Appendix 3. Computational Details

Operator Maps for the Logical Conjunction f₈(u, v)

Computation of εf₈

Computation of Ef₈

Computation of Df₈

Computation of df₈

Computation of rf₈

Computation Summary for Conjunction

Operator Maps for the Logical Equality f₉(u, v)

Computation of εf₉

Computation of Ef₉

Computation of Df₉

Computation of df₉

Computation of rf₉

Computation Summary for Equality

Operator Maps for the Logical Implication f₁₁(u, v)

Computation of εf₁₁

Computation of Ef₁₁

Computation of Df₁₁

Computation of df₁₁

Computation of rf₁₁

Computation Summary for Implication

Operator Maps for the Logical Disjunction f₁₄(u, v)

Computation of εf₁₄

Computation of Ef₁₄

Computation of Df₁₄

Computation of df₁₄

Computation of rf₁₄

Computation Summary for Disjunction

Appendix 4. Source Materials

Appendix 5. Various Definitions of the Tangent Vector

References

References

cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science