Formal Development
The preceding discussion outlined the ideas leading to the differential extension of propositional logic. The next task is to lay out the concepts and terminology needed to describe various orders of differential propositional calculi.
Elementary Notions
Logical description of a universe of discourse begins with a collection of logical signs. For simplicity in a first approach we assume the signs are collected in the form of a finite alphabet, The signs are interpreted as denoting logical features, for example, properties of objects in the universe of discourse or simple propositions about those objects. Corresponding to the alphabet
there is then a set of logical features,
A set of logical features affords a basis for generating an
-dimensional universe of discourse, written
It is useful to consider a universe of discourse as a categorical object incorporating both the set of points
and the set of propositions
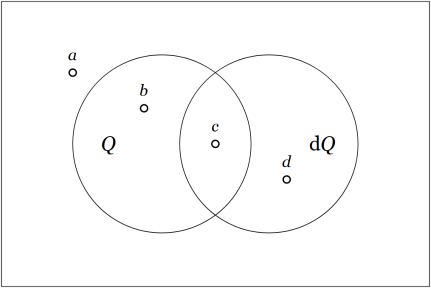
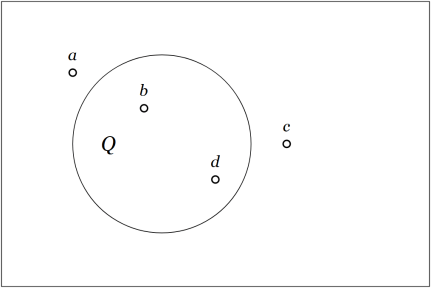
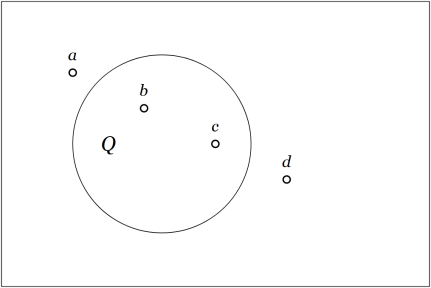
implicit with the ordinary picture of a venn diagram on
features. Accordingly, the universe of discourse
may be regarded as an ordered pair
having the type
and this last type designation may be abbreviated as
or even more succinctly as
For convenience, the data type of a finite set on
elements may be indicated by either one of the equivalent notations,
or
Table 7 summarizes the notations needed to describe ordinary propositional calculi in a systematic fashion.
Resources
- Logic Syllabus
- Differential Logic and Dynamic Systems
- Functional Conception of Propositional Calculus
cc: FB | Differential Logic • Laws of Form • Mathstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science