Suppose we add another individual to our initial universe of discourse, arriving at a three-point universe 
It might be thought that adding one more element to the universe of discourse would allow slightly more complicated relations to be compounded from its basic ingredients, but the truth is that crossing the threshold from a two-point universe to a three-point universe occasions a steep ascent in the complexity of relations generated.
Looking back from the ascent we see that the two-point universe  manifests a type of formal degeneracy (loss of generality) compared with the three-point universe
manifests a type of formal degeneracy (loss of generality) compared with the three-point universe  This is due to the circumstance that the number of “diagonal” pairs, those of the form
This is due to the circumstance that the number of “diagonal” pairs, those of the form  equals the number of “off-diagonal” pairs, those of the form
equals the number of “off-diagonal” pairs, those of the form  so the two-point case exhibits symmetries that will be broken as soon as one adds another element to the universe.
so the two-point case exhibits symmetries that will be broken as soon as one adds another element to the universe.
A universe of three individuals 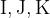 yields exactly nine individual dual relatives or ordered pairs of universe elements:
yields exactly nine individual dual relatives or ordered pairs of universe elements:

It is convenient arrange the pairs in a square array:
![\left( \begin{matrix} \mathrm{I\!:\!I} & \mathrm{I\!:\!J} & \mathrm{I\!:\!K} \\[4pt] \mathrm{J\!:\!I} & \mathrm{J\!:\!J} & \mathrm{J\!:\!K} \\[4pt] \mathrm{K\!:\!I} & \mathrm{K\!:\!J} & \mathrm{K\!:\!K} \end{matrix} \right)](https://s0.wp.com/latex.php?latex=%5Cleft%28+%5Cbegin%7Bmatrix%7D++%5Cmathrm%7BI%5C%21%3A%5C%21I%7D+%26+%5Cmathrm%7BI%5C%21%3A%5C%21J%7D+%26+%5Cmathrm%7BI%5C%21%3A%5C%21K%7D++%5C%5C%5B4pt%5D++%5Cmathrm%7BJ%5C%21%3A%5C%21I%7D+%26+%5Cmathrm%7BJ%5C%21%3A%5C%21J%7D+%26+%5Cmathrm%7BJ%5C%21%3A%5C%21K%7D++%5C%5C%5B4pt%5D++%5Cmathrm%7BK%5C%21%3A%5C%21I%7D+%26+%5Cmathrm%7BK%5C%21%3A%5C%21J%7D+%26+%5Cmathrm%7BK%5C%21%3A%5C%21K%7D++%5Cend%7Bmatrix%7D+%5Cright%29&bg=ffffff&fg=000000&s=1&c=20201002)
There are  dual relatives over this universe of discourse, since each one is formed by choosing a subset of the nine ordered pairs and then “aggregating” them, forming their logical sum, or simply regarding them as a subset. Taking the square array of ordered pairs as a backdrop, any one of the
dual relatives over this universe of discourse, since each one is formed by choosing a subset of the nine ordered pairs and then “aggregating” them, forming their logical sum, or simply regarding them as a subset. Taking the square array of ordered pairs as a backdrop, any one of the  dual relatives may be represented by a square matrix of binary values, a value of
dual relatives may be represented by a square matrix of binary values, a value of  occupying the place of each ordered pair that belongs to the subset and a value of
occupying the place of each ordered pair that belongs to the subset and a value of  occupying the place of each ordered pair that does not belong to the subset in question.
occupying the place of each ordered pair that does not belong to the subset in question.
The matrix representations of the  dual relatives or dyadic relations over the universe
dual relatives or dyadic relations over the universe  are tabulated below according to the following plan:
are tabulated below according to the following plan:
- Since the diagonal and off-diagonal components of the matrices vary independently of each other, the whole set of matrices factors as a product of two smaller sets, making the break along the lines of the corresponding cardinalities,
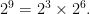
- The eight diagonal matrices are shown in the first row of the display, omitting the off-diagonal zeroes for ease of reading and pattern recognition.
- The
 off-diagonal matrices are shown in the rest of the display, arranged in rank order by increasing numbers of
off-diagonal matrices are shown in the rest of the display, arranged in rank order by increasing numbers of 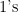 and decreasing numbers of
and decreasing numbers of  suppressing the fixed zeroes along the diagonals to make the changing patterns of
suppressing the fixed zeroes along the diagonals to make the changing patterns of 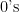 and
and 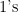 easier to follow.
easier to follow.
- The number of off-diagonal matrices of rank
 is equal to the binomial coefficient
is equal to the binomial coefficient 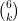 or
or 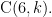 The values of
The values of  are given by the row of Pascal’s Triangle that contains the sequence
are given by the row of Pascal’s Triangle that contains the sequence 
References
- Peirce, C.S. (1880), “On the Algebra of Logic”, American Journal of Mathematics 3, 15–57. Collected Papers (CP 3.154–251), Chronological Edition (CE 4, 163–209).
- Peirce, C.S., Collected Papers of Charles Sanders Peirce, vols. 1–6, Charles Hartshorne and Paul Weiss (eds.), vols. 7–8, Arthur W. Burks (ed.), Harvard University Press, Cambridge, MA, 1931–1935, 1958. Volume 3 : Exact Logic, 1933.
- Peirce, C.S., Writings of Charles S. Peirce : A Chronological Edition, Peirce Edition Project (eds.), Indiana University Press, Bloomington and Indianapolis, IN, 1981–. Volume 4 (1879–1884), 1986.
Resources
