Re: Peirce List Discussion • Helmut Raulien
In discussing Peirce’s concept of a triadic sign relation as existing among objects, signs, and interpretant signs the question arises whether any of the classes so related are classes by themselves, that is, whether there is necessarily anything distinctive about the being of an object, the being of a sign, or the being of an interpretant sign.
Maybe I can clear up a few points about the relational standpoint by resorting to a familiar case of a triadic relation, one I’m guessing we all mastered early in our schooling, namely, the one involved in the operation of subtraction, 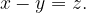 When I was in school we learned a set of quaint terms for the numbers
When I was in school we learned a set of quaint terms for the numbers  in the relation and I wasn’t sure they still taught such things so I checked the web and found a page that described the terms just as I remembered them:
in the relation and I wasn’t sure they still taught such things so I checked the web and found a page that described the terms just as I remembered them:
☞ Maths Is Fun • Subtraction
- The number
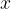 is called the minuend.
is called the minuend.
- The number
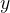 is called the subtrahend.
is called the subtrahend.
- The number
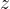 is called the difference.
is called the difference.
So we come to the questions:
- Are minuends a class by themselves?
- Are subtrahends a class by themselves?
- Are differences a class by themselves?
To answer these questions we need to observe the distinction between relational roles and absolute essences (inherent qualities, ontological substances, or permanent properties).
If our notion of number is generous enough to include negative numbers then any number can appear in any one of the three places, so minuend, subtrahend, and difference are relational roles and not absolute essences. We can tell this because it follows from the definition of the subtraction operation.
When it comes time to ask the same questions of objects, signs, and interpretant signs then any hope of a definitive answer must come from the definition of a sign relation we’ve chosen to fit our subject matter.
