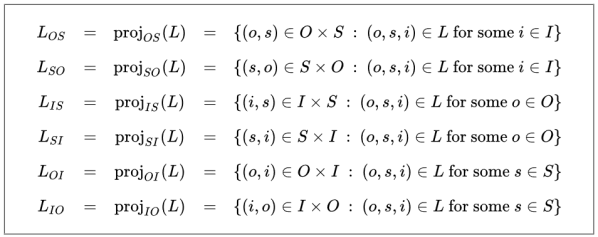Inquiry Into Inquiry

Sign Relations • Semiotic Equivalence Relations 1

Posted on July 1, 2020 by Jon Awbrey

A semiotic equivalence relation (SER) is a special type of equivalence relation arising in the analysis of sign relations. Generally speaking, any equivalence relation induces a partition of the underlying set of elements, known as the domain or space of the relation, into a family of equivalence classes. In the case of a SER the equivalence classes are called semiotic equivalence classes (SECs) and the partition is called a semiotic partition (SEP).

The sign relations $L_\mathrm{A}$ and $L_\mathrm{B}$ have many interesting properties over and above those possessed by sign relations in general. Some of these properties have to do with the relation between signs and their interpretant signs, as reflected in the projections of $L_\mathrm{A}$ and $L_\mathrm{B}$ on the $SI$ -plane, notated as $\mathrm{proj}_{SI} L_\mathrm{A}$ and $\mathrm{proj}_{SI} L_\mathrm{B},$ respectively. The dyadic relations on $S \times I$ induced by these projections are also referred to as the connotative components of the corresponding sign relations, notated as $\mathrm{Con}(L_\mathrm{A})$ and $\mathrm{Con}(L_\mathrm{B}),$ respectively. Tables 6a and 6b show the corresponding connotative components.

A nice property of the sign relations $L_\mathrm{A}$ and $L_\mathrm{B}$ is that their connotative components $\mathrm{Con}(L_\mathrm{A})$ and $\mathrm{Con}(L_\mathrm{B})$ form a pair of equivalence relations on their common syntactic domain $S = I.$ This type of equivalence relation is called a semiotic equivalence relation (SER) because it equates signs having the same meaning to some interpreter.

Each of the semiotic equivalence relations, $\mathrm{Con}(L_\mathrm{A}), \mathrm{Con}(L_\mathrm{B}) \subseteq S \times I \cong S \times S$ partitions the collection of signs into semiotic equivalence classes. This makes for a strong form of representation in that the structure of the interpreters’ common object domain $\{ \mathrm{A}, \mathrm{B} \}$ is reflected or reconstructed, part for part, in the structure of each one’s semiotic partition of the syntactic domain $\{ {}^{\backprime\backprime} \mathrm{A} {}^{\prime\prime}, {}^{\backprime\backprime} \mathrm{B} {}^{\prime\prime}, {}^{\backprime\backprime} \mathrm{i} {}^{\prime\prime}, {}^{\backprime\backprime} \mathrm{u} {}^{\prime\prime} \}.$ But it needs to be observed that the semiotic partitions for interpreters $\mathrm{A}$ and $\mathrm{B}$ are not identical, indeed, they are orthogonal to each other. This allows us to regard the form of these partitions as corresponding to an objective structure or invariant reality, but not the literal sets of signs themselves, independent of the individual interpreter’s point of view.

Information about the contrasting patterns of semiotic equivalence corresponding to the interpreters $\mathrm{A}$ and $\mathrm{B}$ is summarized in Tables 7a and 7b. The form of these Tables serves to explain what is meant by saying the SEPs for $\mathrm{A}$ and $\mathrm{B}$ are orthogonal to each other.

References

Peirce, C.S. (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73. Online.
Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), pp. 40–52. Archive. Journal. Online.

Resources

Document History

Portions of the above article were adapted from the following sources under the GNU Free Documentation License, under other applicable licenses, or by permission of the copyright holders.

cc: Cybernetics • Ontolog • Peirce List (1) (2) • Structural Modeling • Systems Science

Posted in C.S. Peirce, Logic, Logic of Relatives, Mathematics, Peirce, Peirce's Categories, Philosophy, Pragmatic Semiotic Information, Pragmatism, Relation Theory, Semiotics, Sign Relations, Thirdness, Triadic Relations, Triadicity | Tagged C.S. Peirce, Logic, Logic of Relatives, Mathematics, Peirce, Peirce's Categories, Philosophy, Pragmatic Semiotic Information, Pragmatism, Relation Theory, Semiotics, Sign Relations, Thirdness, Triadic Relations, Triadicity | 3 Comments

Sign Relations • Ennotation

Posted on June 29, 2020 by Jon Awbrey

A third aspect of a sign’s complete meaning concerns the reference its objects have to its interpretants, which has no standard name in semiotics. It would be called an induced relation in graph theory or the result of relational composition in relation theory. If an interpretant is recognized as a sign in its own right then its independent reference to an object can be taken as belonging to another moment of denotation, but this neglects the mediational character of the whole transaction in which this occurs. Denotation and connotation have to do with dyadic relations in which the sign plays an active role but here we are dealing with a dyadic relation between objects and interpretants mediated by the sign from an off-stage position, as it were.

As a relation between objects and interpretants mediated by a sign, this third aspect of meaning may be referred to as the ennotation of a sign and the dyadic relation making up the ennotative aspect of a sign relation $L$ may be notated as $\mathrm{Enn}(L).$ Information about the ennotative aspect of meaning is obtained from $L$ by taking its projection on the object-interpretant plane. We may visualize this as the “shadow” $L$ casts on the 2-dimensional space whose axes are the object domain $O$ and the interpretant domain $I.$ The ennotative component of a sign relation $L,$ alternatively written in any of forms, $\mathrm{proj}_{OI} L,$ $L_{OI},$ $\mathrm{proj}_{13} L,$ and $L_{13},$ is defined as follows.

$\begin{matrix} \mathrm{Enn}(L) & = & \mathrm{proj}_{OI} L & = & \{ (o, i) \in O \times I ~:~ (o, s, i) \in L ~\text{for some}~ s \in S \}. \end{matrix}$

As it happens, the sign relations $L_\mathrm{A}$ and $L_\mathrm{B}$ are fully symmetric with respect to exchanging signs and interpretants, so all the data of $\mathrm{proj}_{OS} L_\mathrm{A}$ is echoed unchanged in $\mathrm{proj}_{OI} L_\mathrm{A}$ and all the data of $\mathrm{proj}_{OS} L_\mathrm{B}$ is echoed unchanged in $\mathrm{proj}_{OI} L_\mathrm{B}.$

Tables 5a and 5b show the ennotative components of the sign relations associated with the interpreters $\mathrm{A}$ and $\mathrm{B},$ respectively. The rows of each Table list the ordered pairs $(o, i)$ in the corresponding projections, $\mathrm{Enn}(L_\mathrm{A}), \mathrm{Enn}(L_\mathrm{B}) \subseteq O \times I.$