Inquiry Into Inquiry

Because the examples to follow have been artificially constructed to be as simple as possible, their detailed elaboration can run the risk of trivializing the whole theory of sign relations.  Despite their simplicity, however, these examples have subtleties of their own, and their careful treatment will serve to illustrate many important issues in the general theory of signs.

Imagine a discussion between two people, Ann and Bob, and attend only to the aspects of their interpretive practice involving the use of the following nouns and pronouns:

“Ann”,   “Bob”,   “I”,   “you”.

• The object domain of their discussion is the set of two people
• The sign domain of their discussion is the set of four signs

Ann and Bob are not only the passive objects of linguistic references but also the active interpreters of the language they use.  The system of interpretation (SOI) associated with each language user can be represented in the form of an individual three-place relation known as the sign relation of that interpreter.

In terms of its set-theoretic extension, a sign relation 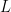is a subset of a cartesian product   The three sets are known as the object domain, the sign domain, and the interpretant domain, respectively, of the sign relation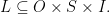

Broadly speaking, the three domains of a sign relation may be any sets at all but the types of sign relations contemplated in formal settings are usually constrained to having 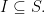  In those situations it becomes convenient to lump signs and interpretants together in a single class called the sign system or the syntactic domain.  In the forthcoming examples and 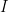are identical as sets, so the same elements manifest themselves in two different roles of the sign relations in question.

When it becomes necessary to refer to the whole set of objects and signs in the union of the domains for a given sign relation we will call this set the World of 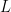and write

To facilitate an interest in the formal structures of sign relations and to keep notations as simple as possible as the examples become more complicated, it serves to introduce the following general notations:

Introducing a few abbreviations for use in this Example, we have the following data:

In the present example,

Tables 1a and 1b show the sign relations associated with the interpreters 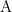and 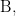respectively.  In this arrangement the rows of each Table list the ordered triples of the form belonging to the corresponding sign relations,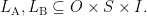

These Tables codify a rudimentary level of interpretive practice for the agents 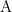and and provide a basis for formalizing the initial semantics appropriate to their common syntactic domain.  Each row of a Table lists an object and two co-referent signs, making up an ordered triple of the form called an elementary relation, that is, one element of the relation’s set-theoretic extension.

Already in this elementary context, there are several different meanings that might attach to the project of a formal semiotics, or a formal theory of meaning for signs.  In the process of discussing these alternatives, it is useful to introduce a few terms occasionally used in the philosophy of language to point out the needed distinctions.  That is the task we’ll turn to next.

References

• Peirce, C.S. (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73.  Online.
• Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), pp. 40–52.  Archive.  Journal.  Online.

Resources

• Semeiotic
• Logic Syllabus
• Sign Relations
• Triadic Relations
• Relation Theory

Document History

Portions of the above article were adapted from the following sources under the GNU Free Documentation License, under other applicable licenses, or by permission of the copyright holders.

• Sign Relation • OEIS Wiki
• Sign Relation • InterSciWiki
• Sign Relation • MyWikiBiz
• Sign Relation • PlanetMath
• Sign Relation • Wikiversity
• Sign Relation • Wikipedia

cc: Cybernetics • Ontolog • Peirce List (1) (2) • Structural Modeling • Systems Science

Re: Sign Relations • Discussion 4
Re: Peirce List • Jon Awbrey • Gary Fuhrman • Jon Alan Schmidt • Jon Awbrey

The transformative idea in Peirce’s case of the French interpreter is not the convertibility of term logic, propositional logic, and monadic predicate logic — a commonplace of logic from the time of Aristotle, if not in those words, obscured only by the false subtleties of the Frege-Russell tradition, though even Quine was woke enough in time to write a nice essay on it — but rather the transformation from interpreter models to interpretant models of semiosis.  The latter models are what Peirce and all in his train require for constructing abstract formal theories neutral on psychologism, materialism, biologism, and various other all too stolid -isms.

There’s more discussion of Peirce’s passage to the interpretant at the following locations.

• Inquiry Driven Systems • C’est Moi
• Information = Comprehension × Extension • Selection 18

References

• Peirce, C.S. (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73.  Online.
• Peirce, C.S., Writings of Charles S. Peirce : A Chronological Edition, Peirce Edition Project (eds.), Indiana University Press, Bloomington and Indianapolis, IN, 1981–.  Cited as (CE volume, page).

Resources

• Semeiotic
• Logic Syllabus
• Sign Relations
• Triadic Relations
• Relation Theory

cc: Cybernetics • Ontolog • Peirce List (1) (2) • Structural Modeling • Systems Science

Re: Peirce List • Edwina Taborsky

A note on a couple of recurring themes may be useful at this point.

1. Peirce’s “metaphorical argument” for transforming discussion of interpretive agents, whether individuals or communities, to discussion of interpretant signs is as follows.

There’s additional discussion of this passage at the following locations.

• Inquiry Driven Systems • C’est Moi
• Information = Comprehension × Extension • Selection 18

2. When we employ mathematical models to describe any domain of phenomena, we are always proceeding hypothetically and tentatively, and the modality of all mathematics, in its own right, is the possible.  That is because mathematical existence is existence in the modest sense of “whatever’s not inconsistent”.  In the idiom, “It’s would-be’s all the way down.”  In effect the ordinary scales of modality are flattened down to one mode, to wit, Be ♭.  It is not until we take the risk of acting on our abduced model that we encounter genuine brute force Secondness.

References

• Peirce, C.S. (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73.  Online.
• Peirce, C.S., Writings of Charles S. Peirce : A Chronological Edition, Peirce Edition Project (eds.), Indiana University Press, Bloomington and Indianapolis, IN, 1981–.  Cited as (CE volume, page).

Resources

• Semeiotic
• Logic Syllabus
• Sign Relations
• Triadic Relations
• Relation Theory

cc: Cybernetics • Ontolog • Peirce List (1) (2) • Structural Modeling • Systems Science

Re: Sign Relations • Definition
Re: Ontolog Forum • Alex Shkotin (1) (2)

Regarding Peirce’s definition of a sign linked above, Alex Shkotin writes:

Dear Alex,

Thanks for your comment.  It points to a problem lurking in the wings through all these discussions, so let’s nudge it on stage and throw a better light on it.

I remember my first formal logic prof in college being rather adamant about the difference between a logical formula, which supposedly bore its “logical form” on its sleeve — I recall the very figure he used — and any of its diverse and sundry natural language paraphrases.  As time wore on I would reconfigure many of the lessons impressed on me in those days, but that one has stuck, I’m guessing because it goes without saying in mathematical and scientific practice.

This treble clef, to vary the figure — forms as objects, formulas as signs, and paraphrases as interpretant signs — is the key to a fundamental theme.

A very wide field of discussion opens up at this point.  To begin we have the logical jump from forms to formulas and the semiotic drift from formulas to paraphrases.  Further on we’ll encounter a range of tensions between formal and informal contexts of inquiry.

Susan Awbrey and I discussed a related set of issues in our “Conceptual Barriers” paper.  Here is how we set up our treatment of three problematics.

• Problematic 1 is the tension that arises along a dimension of increasing formalization in our mental models of the world, between what we may call the ‘informal context’ of real-world practice and the ‘formal context’ of specialized study.
• Problematic 2 is the difficulty in communication that is created by differing mental models of the world, in other words, by the tendency among groups of specialists to form internally coherent but externally disparate systems of mental images.
• Problematic 3 is a special type of communication difficulty that commonly arises between the ‘Two Cultures’ of the scientific and the humanistic disciplines.  A significant part of the problem derives from the differential emphasis that each group places on its use of symbolic and conceptual systems, limiting itself to either the denotative or the connotative planes of variation, but seldom integrating the two.

Please excuse the sweeping preamble.  It wasn’t meant to sweep your observations under the rug — it’s just so many discussions here and there on the web in recent days are reminding me of the larger designs beyond my more mundane focus on brass tacks matters.  I’ll bring this all back to bear on the everyday life of signs the next chance I get.

References

• Awbrey, S.M., and Awbrey, J.L. (2001), “Conceptual Barriers to Creating Integrative Universities”, Organization : The Interdisciplinary Journal of Organization, Theory, and Society 8(2), Sage Publications, London, UK, pp. 269–284.  Abstract.  Online.
• Peirce, C.S. (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73.  Online.

Resources

• Semeiotic
• Logic Syllabus
• Sign Relations
• Triadic Relations
• Relation Theory

cc: Cybernetics • Ontolog • Peirce List (1) (2) • Structural Modeling • Systems Science

There is a close relationship between the pragmatic theory of signs and the pragmatic theory of inquiry.  In fact, the correspondence between the two studies exhibits so many congruences and parallels it is often best to treat them as integral parts of one and the same subject.  In a very real sense, inquiry is the process by which sign relations come to be established and continue to evolve.  In other words, inquiry, “thinking” in its best sense, “is a term denoting the various ways in which things acquire significance” (John Dewey).  Thus, there is an active and intricate form of cooperation that needs to be appreciated and maintained between these converging modes of investigation.  Its proper character is best understood by realizing that the theory of inquiry is adapted to study the developmental aspects of sign relations, a subject which the theory of signs is specialized to treat from structural and comparative points of view.

References

• Charles S. Peirce (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73.  Online.
• Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), pp. 40–52.  Archive.  Journal.  Online.

Resources

• Inquiry
• Semeiotic
• Logic Syllabus
• Sign Relations
• Triadic Relations
• Relation Theory

Document History

Portions of the above article were adapted from the following sources under the GNU Free Documentation License, under other applicable licenses, or by permission of the copyright holders.

• Sign Relation • OEIS Wiki
• Sign Relation • InterSciWiki
• Sign Relation • MyWikiBiz
• Sign Relation • Wikiversity
• Sign Relation • Wikipedia

cc: Cybernetics • Ontolog • Peirce List (1) (2) • Structural Modeling • Systems Science

Re: Cybernetics • Bernard C.E. Scott
Re: Sign Relations • Definition

Regarding Peirce’s definition of a sign given in the previous post, Bernard Scott writes:

It is very helpful [to] distinguish Peirce’s formal semiotic (his logic) from psychological, and by extension, ‘biosemiotic’ understandings of ‘sign’.

Dear Bernard,

You raise a very important point.  It is critical to distinguish the abstract theory from its concrete applications.  The power of a great theory lies in the diversity of its applications.  But that very power comes with a warning, as the diversity it generates can be the source of dispute and dissension among its appliers and interpreters.

We all know the parable of the seven sightless sages and the polymorphous pachyderm they ponder, so I don’t need to spend a lot of words on the moral of that story here.  But it may be useful to say more about the major misunderstandings occasioned by, the schisms, sects, and splinter groups spawned by Peirce’s extremely general and powerful theory of triadic sign relations.  I’ll attend to that when I next get a chance.

Reference

• Charles S. Peirce (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73.  Online.

Resources

• Semeiotic
• Logic Syllabus
• Sign Relations
• Triadic Relations
• Relation Theory

cc: Cybernetics • Ontolog • Peirce List (1) (2) • Structural Modeling • Systems Science