Re: Category Theory • Henry Story
- HS:
- I think in this 2020 Applied Category Theory talk by Rocco Gangle, A Generic Figures Reconstruction of Peirce’s Existential Graphs (Alpha), he is looking at showing how Peirce’s work can be expressed in terms of Category Theory.
I looked at that once, I think. I seem to recall he is still using the planar maps which I consider the mark of a novice, but I will give it another look.
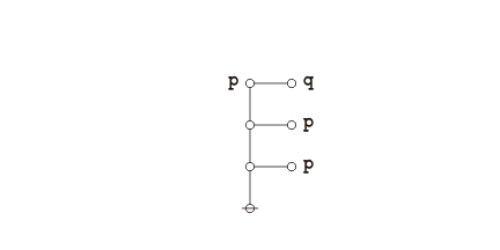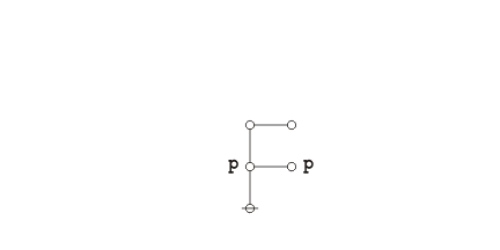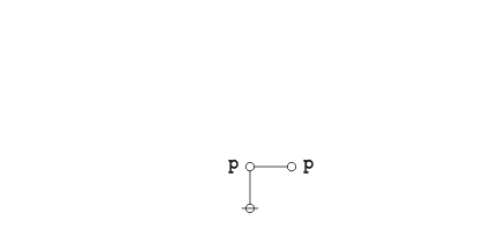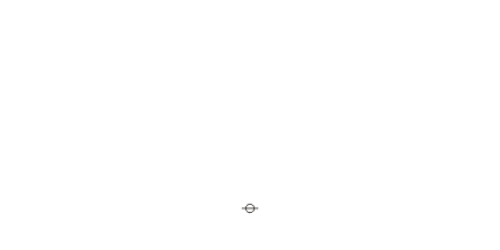
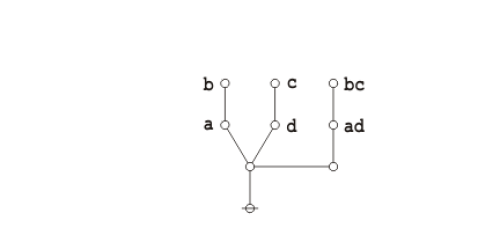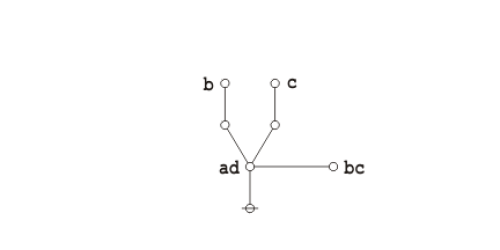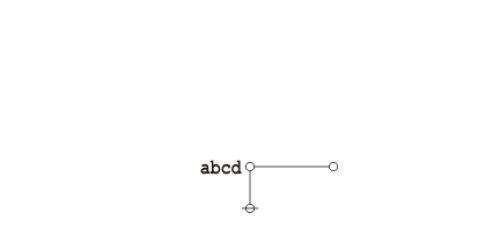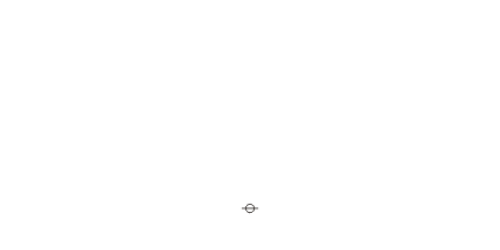
Okay, I see he introduces forests about half-way through, that’s a good thing, but he’s not up to cacti yet, which is something I found necessary early on for the sake of both conceptual and computational efficiency. So there’s a few things I will need to explain …
I started working on logical graphs early in my undergrad years, after my encounter with Peirce’s Collected Papers, quickly followed by my study of Spencer Brown’s Laws of Form, and from the outset trying everything I could hack by way of syntax handlers and theorem provers in every mix of languages and machines I got my hands on. That combination of forces and media summed to form my current direction.
Peirce broke ground and laid the groundwork, Spencer Brown shored up the infrastructure of primary arithmetic and leveled the proving grounds to facilitate equational inference, and a host of computers supplied the real-world recalcitrance of matter, the resistance to facile simplicity, and the rebuke of all too facile reductionism.
Resources
- Logical Graphs
- Minimal Negation Operators
- Logical Graphs • Introduction
- Logical Graphs • Development
- Logic Syllabus • Zeroth Order Logic
- Survey of Animated Logical Graphs
cc: Peirce List (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15) (16) (17)
cc: Category Theory • Cybernetics (1) (2) • Ontolog Forum (1) (2)
cc: Structural Modeling (1) (2) • Systems Science (1) (2)
cc: FB | Logical Graphs • Laws of Form