Re: Richard J. Lipton • Logical Complexity Of Proofs
Re: Animated Logical Graphs • (35) (36) (37) (38) (39) (40)
Last time we looked at a formula of propositional logic Leibniz called a Praeclarum Theorema (PT). We don’t concur it’s a theorem, of course, until there’s a proof it’s identically true and Leibniz gave an argument to demonstrate that. Written out in one of our more current formalisms, PT takes the following form.

Somewhat in the spirit of Reduced Instruction Set Computing, we reformulated PT in a propositional calculus using just two primitive operations, writing the logical negation of a proposition 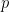 as
as  and the logical conjunction of two propositions
and the logical conjunction of two propositions 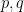 as
as  That gave us a text string in teletype parentheses and proposition letters, formatted two ways below.
That gave us a text string in teletype parentheses and proposition letters, formatted two ways below.

Our next transformation of the theorem’s expression exploits a standard correspondence in combinatorics and computer science between parenthesized symbol strings and trees with symbols attached to the nodes.

We can see the correspondence between text and tree in the case of PT by starting at the root of the tree and reading off the characters of the text string as we traverse the edges and nodes of the tree in the following manner. The initial  tells us to ascend the first edge, the next
tells us to ascend the first edge, the next  tells us to ascend the next edge on the left, where we find the letter
tells us to ascend the next edge on the left, where we find the letter 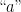 from the string checks with the letter
from the string checks with the letter 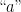 attached to the node of the tree where we are. Another
attached to the node of the tree where we are. Another  takes us up another edge, where we find the letter
takes us up another edge, where we find the letter 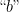 from the string checks with the letter
from the string checks with the letter 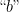 on the current tree node. Reading the first
on the current tree node. Reading the first 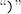 on the string entitles us to descend an edge and reading another
on the string entitles us to descend an edge and reading another 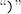 gives us licence to descend another. The way of things is most likely clear by this point — at any rate, I leave the exercise to the reader.
gives us licence to descend another. The way of things is most likely clear by this point — at any rate, I leave the exercise to the reader.
On the scene of the general correspondence between formulas and graphs the action may be summed up as follows. The tree, called a parse tree or parse graph, is constructed in the process of checking whether the text string is syntactically well-formed, in other words, whether it satisfies the prescriptions of the associated formal grammar and is therefore a member in good standing of the prescribed formal language. If the text string checks out, grammatically speaking, we call it a traversal string of the corresponding parse graph, because it can be reconstructed from the graph by a process like that illustrated above called traversing the graph.
To be continued …
Reference
- Leibniz, Gottfried W. (1679–1686?), “Addenda to the Specimen of the Universal Calculus”, pp. 40–46 in G.H.R. Parkinson (ed., trans., 1966), Leibniz : Logical Papers, Oxford University Press, London, UK.
Praeclarum Theorema
Resources
Applications
cc: Cybernetics • Ontolog • Peirce (1) (2) (3) (4) (5) (6) • Structural Modeling • Systems


