Inquiry Into Inquiry

Precursors Of Category Theory • 1

Posted on May 25, 2024 by Jon Awbrey

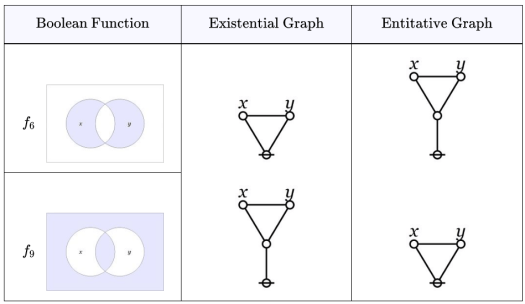
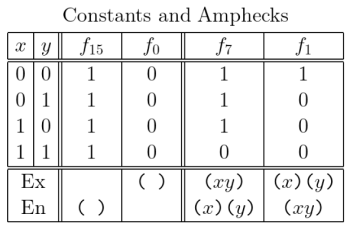
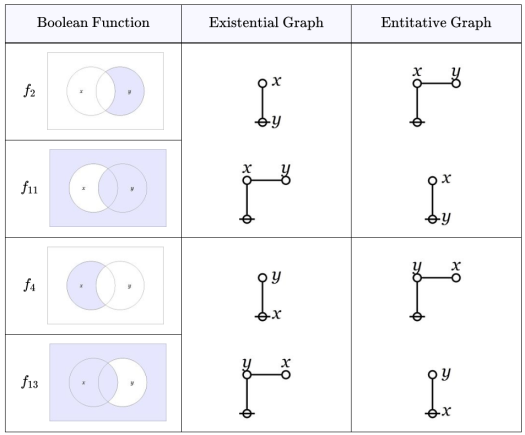
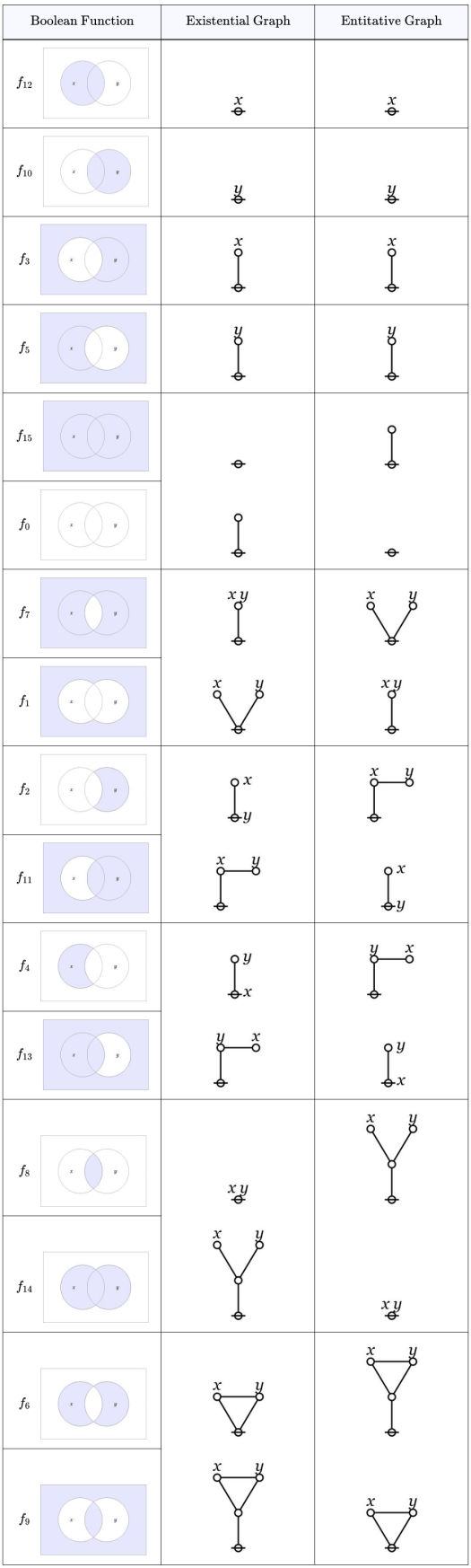
A few years ago I began a sketch on the “Precursors of Category Theory”, tracing the continuities of the category concept from Aristotle, to Kant and Peirce, through Hilbert and Ackermann, to contemporary mathematical practice. My notes on the project are still very rough and incomplete but I find myself returning to them from time to time.

Preamble

Now the discovery of ideas as general as these is chiefly the willingness to make a brash or speculative abstraction, in this case supported by the pleasure of purloining words from the philosophers: “Category” from Aristotle and Kant, “Functor” from Carnap (Logische Syntax der Sprache), and “natural transformation” from then current informal parlance.

— Saunders Mac Lane • Categories for the Working Mathematician

Resources

cc: FB | Peirce Matters • Laws of Form • Ma^thstodon • Ontolog • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in Abstraction, Ackermann, Aristotle, C.S. Peirce, Carnap, Category Theory, Hilbert, Kant, Logic, Logic of Relatives, Mathematics, Peirce, Peirce's Categories, Relation Theory, Saunders Mac Lane, Sign Relations, Type Theory | Tagged Abstraction, Ackermann, Aristotle, C.S. Peirce, Carnap, Category Theory, Hilbert, Kant, Logic, Logic of Relatives, Mathematics, Peirce, Peirce's Categories, Relation Theory, Saunders Mac Lane, Sign Relations, Type Theory | 3 Comments

Survey of Precursors Of Category Theory • 5

Posted on May 24, 2024 by Jon Awbrey

A few years ago I began a sketch on the “Precursors of Category Theory”, tracing the continuities of the category concept from Aristotle, to Kant and Peirce, through Hilbert and Ackermann, to contemporary mathematical practice. A Survey of resources on the topic is given below, still very rough and incomplete, but perhaps a few will find it of use.

Background

Blog Series

Notes On Categories • (1)
Precursors Of Category Theory • (1) • (2) • (3) • (4) • (5) • (6)

Discussions • (1) • (2) • (3)

Categories à la Peirce

C.S. Peirce • A Guess at the Riddle

Peirce’s Categories • (1) • (2) • (3) • (4) • (5) • (6) • (7) • (8) • (9) • (10) • (11) • (12) • (13) • (14) • (15) • (16) • (17) • (18) • (19) • (20) • (21)

C.S. Peirce and Category Theory • (1) • (2) • (3) • (4) • (5) • (6) • (7) • (8)

cc: FB | Peirce Matters • Laws of Form • Ma^thstodon • Ontolog • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in Abstraction, Ackermann, Analogy, Aristotle, C.S. Peirce, Carnap, Category Theory, Diagrams, Foundations of Mathematics, Functional Logic, Hilbert, History of Mathematics, Hypostatic Abstraction, Kant, Logic, Mathematics, Peirce, Propositions As Types Analogy, Relation Theory, Saunders Mac Lane, Semiotics, Type Theory, Universals | Tagged Abstraction, Ackermann, Analogy, Aristotle, C.S. Peirce, Carnap, Category Theory, Diagrams, Foundations of Mathematics, Functional Logic, Hilbert, History of Mathematics, Hypostatic Abstraction, Kant, Logic, Mathematics, Peirce, Propositions As Types Analogy, Relation Theory, Saunders Mac Lane, Semiotics, Type Theory, Universals | 10 Comments

Transformations of Logical Graphs • Discussion 1

Posted on May 22, 2024 by Jon Awbrey

Re: Laws of Form • Mauro Bertani

Dear Mauro,

The couple of pages linked below give the clearest and quickest introduction I’ve been able to manage so far when it comes to the elements of logical graphs, at least, in the way I’ve come to understand them. The first page gives a lot of detail by way of motivation and computational implementation, so you could easily put that off till you feel a need for it. The second page lays out the precise axioms or initials I use — the first algebraic axiom varies a bit from Spencer Brown for a better fit with C.S. Peirce — and also shows the parallels between the dual interpretations.

Additional Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Interpretive Duality, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Visualization | Tagged Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Interpretive Duality, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Visualization | 2 Comments

Transformations of Logical Graphs • 14

Posted on May 21, 2024 by Jon Awbrey

Semiotic Transformations

Re: Transformations of Logical Graphs • (8) • (9) • (10) • (11) • (12) • (13)

Completing our scan of the Table in Episode 8, the last orbit up for consideration contains the logical graphs for the boolean functions $f_{6}$ and $f_{9}.$

$\text{Interpretive Duality} \stackrel{_\bullet}{} \text{Difference and Equality}$

The boolean functions $f_{6}$ and $f_{9}$ are known as logical difference and logical equality, respectively. The values taken by $f_{6}$ and $f_{9}$ for each pair of arguments $(x, y)$ in $\mathbb{B} \times \mathbb{B}$ and the text expressions for their logical graphs are given in the following Table.

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Transformations of Logical Graphs • 13

Posted on May 18, 2024 by Jon Awbrey

Semiotic Transformations

Re: Transformations of Logical Graphs • (8) • (9) • (10) • (11) • (12)

Continuing our scan of the Table in Episode 8, the next orbit contains the logical graphs for the boolean functions $f_{8}$ and $f_{14}.$

$\text{Interpretive Duality} \stackrel{_\bullet}{} \text{Conjunction and Disjunction}$

The boolean functions $f_{8}$ and $f_{14}$ are called logical conjunction and logical disjunction, respectively. The values taken by $f_{8}$ and $f_{14}$ for each pair of arguments $(x, y)$ in $\mathbb{B} \times \mathbb{B}$ and the text expressions for their logical graphs are given in the following Table.

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Transformations of Logical Graphs • 12

Posted on May 16, 2024 by Jon Awbrey

Semiotic Transformations

Re: Transformations of Logical Graphs • (8) • (9) • (10) • (11)
Re: Interpretive Duality as Sign Relation • Orbit Order

Taking from our wallets an old schedule of orbits, let’s review the classes of logical graphs we’ve covered so far.

Self-Dual Logical Graphs

Four orbits of self‑dual logical graphs, $x, y, \texttt{(} x \texttt{)}, \texttt{(} y \texttt{)},$ were discussed in Episode 9.

The logical graphs $x, y, \texttt{(} x \texttt{)}, \texttt{(} y \texttt{)}$ denote the boolean functions $f_{12}, f_{10}, f_{3}, f_{5},$ in that order. The value of each function $f$ at each point $(x, y)$ in $\mathbb{B} \times \mathbb{B}$ is shown in the Table above.

Constants and Amphecks

Two orbits of logical graphs called constants and amphecks were discussed in Episode 10.

The constant logical graphs denote the constant functions

$f_{0} : \mathbb{B} \times \mathbb{B} \to 0 \quad \text{and} \quad f_{15} : \mathbb{B} \times \mathbb{B} \to 1.$

Under $\mathrm{Ex}$ the logical graph whose text form is “ ” denotes the function $f_{15}$
and the logical graph whose text form is $``\texttt{(} ~ \texttt{)}"$ denotes the function $f_{0}.$
Under $\mathrm{En}$ the logical graph whose text form is “ ” denotes the function $f_{0}$
and the logical graph whose text form is $``\texttt{(} ~ \texttt{)}"$ denotes the function $f_{15}.$

The ampheck logical graphs denote the ampheck functions

$f_{1}(x, y) = \textsc{nnor}(x, y) \quad \text{and} \quad f_{7}(x, y) = \textsc{nand}(x, y).$

Under $\mathrm{Ex}$ the logical graph $\texttt{(} xy \texttt{)}$ denotes the function $f_{7}(x, y) = \textsc{nand}(x, y)$
and the logical graph $\texttt{(} x \texttt{)(} y \texttt{)}$ denotes the function $f_{1}(x, y) = \textsc{nnor}(x, y).$
Under $\mathrm{En}$ the logical graph $\texttt{(} xy \texttt{)}$ denotes the function $f_{1}(x, y) = \textsc{nnor}(x, y)$
and the logical graph $\texttt{(} x \texttt{)(} y \texttt{)}$ denotes the function $f_{7}(x, y) = \textsc{nand}(x, y).$

Subtractions and Implications

The logical graphs called subtractions and implications were discussed in Episode 11.

The subtraction logical graphs denote the subtraction functions

$f_{2}(x, y) = y \lnot x \quad \text{and} \quad f_{4}(x, y) = x \lnot y.$

The implication logical graphs denote the implication functions

$f_{11}(x, y) = x \Rightarrow y \quad \text{and} \quad f_{13}(x, y) = y \Rightarrow x.$

Under the action of the $\mathrm{En} \leftrightarrow \mathrm{Ex}$ duality the logical graphs for the subtraction $f_{2}$ and the implication $f_{11}$ fall into one orbit while the logical graphs for the subtraction $f_{4}$ and the implication $f_{13}$ fall into another orbit, making these two partitions of the four functions orthogonal or transversal to each other.

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Transformations of Logical Graphs • 11

Posted on May 15, 2024 by Jon Awbrey

Semiotic Transformations

Re: Transformations of Logical Graphs • (8) • (9) • (10)

Continuing our scan of the Table in Episode 8, the next two orbits contain the logical graphs for the boolean functions $f_{2}, f_{11}, f_{4}, f_{13},$ in that order. A first glance shows the two orbits have surprisingly intricate structures and relationships to each other — let’s isolate that section for a closer look.

$\text{Interpretive Duality} \stackrel{_\bullet}{} \text{Subtractions and Implications}$

The boolean functions $f_{2}$ and $f_{4}$ are called subtraction functions.
The boolean functions $f_{11}$ and $f_{13}$ are called implication functions.

The logical graphs for $f_{2}$ and $f_{11}$ are dual to each other.
The logical graphs for $f_{4}$ and $f_{13}$ are dual to each other.

The values of the subtraction and implication functions for each $(x, y) \in \mathbb{B} \times \mathbb{B}$ and the text expressions for their logical graphs are given in the following Table.

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Transformations of Logical Graphs • 10

Posted on May 14, 2024 by Jon Awbrey

Semiotic Transformations

Re: Transformations of Logical Graphs • (4) • (5) • (6) • (7) • (8) • (9)

After the four orbits of self‑dual logical graphs we come to six orbits of dual pairs. In no particular order of importance, we may start by considering the following two.

The logical graphs for the constant functions $f_{15}$ and $f_{0}$ are dual to each other.
The logical graphs for the ampheck functions $f_{7}$ and $f_{1}$ are dual to each other.

The values of the constant and ampheck functions for each $(x, y) \in \mathbb{B} \times \mathbb{B}$ and the text expressions for their logical graphs are given in the following Table.

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Transformations of Logical Graphs • 9

Posted on May 13, 2024 by Jon Awbrey

Semiotic Transformations

Re: Transformations of Logical Graphs • (4) • (5) • (6) • (7) • (8)

Last time we took up the four singleton orbits in the action of $T$ on $X$ and saw each consists of a single logical graph which $T$ fixes, preserves, or transforms into itself. On that account those four logical graphs are said to be self‑dual or $T$ ‑invariant.

In general terms, it is useful to think of the entitative and existential interpretations as two formal languages which happen to use the same set of signs, each in its own way, to denote the same set of formal objects. Then $T$ defines the translation between languages and the self‑dual logical graphs are the points where the languages coincide, where the same signs denote the same objects in both. Such constellations of “fixed stars” are indispensable to navigation between languages, as every argot‑naut discovers in time.

Returning to the case at hand, where $T$ acts on a selection of 16 logical graphs for the 16 boolean functions on two variables, the following Table shows the values of the denoted boolean function $f : \mathbb{B} \times \mathbb{B} \to \mathbb{B}$ for each of the self‑dual logical graphs.

The functions indexed here as $f_{12}$ and $f_{10}$ are known as the coordinate projections $(x, y) \mapsto x$ and $(x, y) \mapsto y$ on the first and second coordinates, respectively, and the functions indexed as $f_{3}$ and $f_{5}$ are the negations $(x, y) \mapsto \tilde{x}$ and $(x, y) \mapsto \tilde{y}$ of those projections, respectively.

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Transformations of Logical Graphs • 8

Posted on May 12, 2024 by Jon Awbrey

Semiotic Transformations

Re: Transformations of Logical Graphs • (4) • (5) • (6) • (7)

Turning again to our Table of Orbits let’s see what we can learn about the structure of the sign relational system in view.

As we saw in Episode 2, the transformation group $T = \{ 1, t \}$ partitions the set $X$ of 16 logical graphs and also the set $O$ of 16 boolean functions into 10 orbits, all together amounting to 4 singleton orbits and 6 doubleton orbits.

Points in singleton orbits are called fixed points of the transformation group $T : X \to X$ since they are left unchanged, or changed into themselves, by all group actions. Viewed in the frame of the sign relation $L \subseteq O \times X \times X,$ where the transformations in $T$ are literally translations in the linguistic sense, these $T$ -invariant graphs have the same denotations in $O$ for both Existential Interpreters and Entitative Interpreters.

$\text{Interpretive Duality as Sign Relation} \stackrel{_\bullet}{} \text{Orbit Order}$

Resources

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

	Survey of Semiotics,… on Sign Relations • Graphical…
	Sign Relations • Gra… on Survey of Semiotics, Semiosis,…
	Survey of Semiotics,… on Sign Relations • Graphical…
	Sign Relations • Gra… on Survey of Semiotics, Semiosis,…
	Jon Awbrey on Sign Relations • Definiti…
	Jon Awbrey on Sign Relations • Definiti…
	Jon Awbrey on Sign Relations • Definiti…
	Survey of Semiotics,… on Sign Relations • Semiotic Equi…
	Survey of Semiotics,… on Sign Relations • Semiotic Equi…
	Sign Relations • Sem… on Survey of Semiotics, Semiosis,…

Preamble

Resources

Share this:

Background

Blog Series

Categories à la Peirce

Share this:

Additional Resources

Share this:

Semiotic Transformations

Resources

Share this:

Semiotic Transformations

Resources

Share this:

Semiotic Transformations

Self-Dual Logical Graphs

Constants and Amphecks

Subtractions and Implications

Resources

Share this:

Semiotic Transformations

Resources

Share this:

Semiotic Transformations

Resources

Share this:

Semiotic Transformations

Resources

Share this:

Semiotic Transformations

Resources

Share this:

Elsewhere

Blogroll

Follow Blog via Email

Recent Posts

Recent Comments

Archives

Blog Stats

Categories

Logic, Mathematics, Philosophy

Current Events

Meta