Inquiry and Analogy • Aristotle’s “Apagogy” • Abductive Reasoning
Peirce’s notion of abductive reasoning is derived from Aristotle’s treatment of it in the Prior Analytics. Aristotle’s discussion begins with an example which may seem incidental but the question and its analysis are echoes of the investigation pursued in one of Plato’s Dialogue, the Meno. It concerns nothing less than the possibility of knowledge and the relationship between knowledge and virtue, or between their objects, the true and the good. It is not just because it forms a recurring question in philosophy, but because it preserves a close correspondence between its form and its content, that we shall find this example increasingly relevant to our study.
We have Reduction (απαγωγη, abduction): (1) when it is obvious that the first term applies to the middle, but that the middle applies to the last term is not obvious, yet nevertheless is more probable or not less probable than the conclusion; or (2) if there are not many intermediate terms between the last and the middle; for in all such cases the effect is to bring us nearer to knowledge.
(1) E.g., let A stand for “that which can be taught”, B for “knowledge”, and C for “morality”. Then that knowledge can be taught is evident; but whether virtue is knowledge is not clear. Then if BC is not less probable or is more probable than AC, we have reduction; for we are nearer to knowledge for having introduced an additional term, whereas before we had no knowledge that AC is true.
(2) Or again we have reduction if there are not many intermediate terms between B and C; for in this case too we are brought nearer to knowledge. E.g., suppose that D is “to square”, E “rectilinear figure”, and F “circle”. Assuming that between E and F there is only one intermediate term — that the circle becomes equal to a rectilinear figure by means of lunules — we should approximate to knowledge.
Aristotle, “Prior Analytics” 2.25, Hugh Tredennick (trans.)
A few notes on the reading may be helpful. The Greek text seems to imply a geometric diagram, in which directed line segments AB, BC, AC indicate logical relations between pairs of terms taken from A, B, C. We have two options for reading the line labels, either as implications or as subsumptions, as in the following two paradigms for interpretation.
In the latter case, is read as
that is,
or
The method of abductive reasoning bears a close relation to the sense of reduction in which we speak of one question reducing to another. The question being asked is “Can virtue be taught?” The type of answer which develops is as follows.
If virtue is a form of understanding, and if we are willing to grant that understanding can be taught, then virtue can be taught. In this way of approaching the problem, by detour and indirection, the form of abductive reasoning is used to shift the attack from the original question, whether virtue can be taught, to the hopefully easier question, whether virtue is a form of understanding.
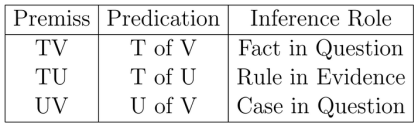
The logical structure of the process of hypothesis formation in the first example follows the pattern of “abduction to a case”, whose abstract form is diagrammed and schematized in Figure 5.
The sense of the Figure is explained by the following assignments.
Abduction from a Fact to a Case proceeds according to the following schema.
Resources
- Logic Syllabus
- Boolean Function
- Boolean-Valued Function
- Logical Conjunction
- Minimal Negation Operator
- Functional Logic • Part 1 • Part 2 • Part 3
- Cactus Language • Part 1 • Part 2 • Part 3 • References • Document History
cc: FB | Peirce Matters • Laws of Form • Mathstodon • Ontolog • Academia.edu (1) (2)
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science





Pingback: Survey of Abduction, Deduction, Induction, Analogy, Inquiry • 2 | Inquiry Into Inquiry
Pingback: Survey of Abduction, Deduction, Induction, Analogy, Inquiry • 3 | Inquiry Into Inquiry