Inquiry Into Inquiry

Paradisaical Logic and the After Math • Comment 2

Posted on April 7, 2021 by Jon Awbrey

Dear Mauro,

My access to the internet is limited today — maybe I can make a start toward addressing your comments by linking to an article on “sole sufficient operators” in boolean algebra and propositional calculus.

Sole Sufficient Operator

There’s more information about Peirce’s “amphecks”, tantamount to what we now call Nand and Nnor, in the following article.

Ampheck

Resources

cc: Cybernetics • Ontolog • Peirce List (1) (2) • Structural Modeling • Systems Science
cc: FB | Logical Graphs • Laws of Form

Posted in Amphecks, C.S. Peirce, Critical Thinking, Inquiry, Logic, Logic of Relatives, Logical Graphs, Logical Reflexion, Mathematics, Peirce, Relation Theory, Second Intentions, Semiotics, Sign Relations, Truth Theory, Visualization | Tagged Amphecks, C.S. Peirce, Critical Thinking, Inquiry, Logic, Logic of Relatives, Logical Graphs, Logical Reflexion, Mathematics, Peirce, Relation Theory, Second Intentions, Semiotics, Sign Relations, Truth Theory, Visualization | 1 Comment

Animated Logical Graphs • 70

Posted on April 7, 2021 by Jon Awbrey

Re: Richard J. Lipton • The Art Of Math
Re: Animated Logical Graphs • (57) • (58) • (59) • (60) • (61) • (62) • (63) • (64) • (65) • (66) • (69)

Our study of the duality between entitative and existential interpretations of logical graphs has brought to light its fully sign-relational character. We can see this in the sign relation linking an object domain with two sign domains, whose signs denote the objects in two distinct ways. We illustrated the general principle using an object domain consisting of the sixteen boolean functions on two variables and a pair of sign domains consisting of representative logical graphs for those functions, as shown in the following Table.

$\text{Peirce Duality as Sign Relation}$

Column 1 shows the object domain $O$ as the set of 16 boolean functions on 2 variables.
Column 2 shows the sign domain $S$ as a representative set of logical graphs denoting the objects in $O$ according to the existential interpretation.
Column 3 shows the interpretant domain $I$ as the same set of logical graphs denoting the objects in $O$ according to the entitative interpretation.

Additional aspects of the sign relation’s structure can be brought out by sorting the Table in accord with the orbits induced on the object domain by the action of the transformation group inherent in the dual interpretations. Performing that sort produces the following Table.

$\text{Peirce Duality as Sign Relation} \stackrel{_\bullet}{} \text{Orbit Order}$

That’s enough bytes to chew on for one post — we’ll extract more information from the Tables next time.

Resources

cc: Peirce List (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14) (15)
cc: Structural Modeling (1) (2) • Systems Science (1) (2)
cc: Cybernetics (1) (2) • Ontolog Forum (1) (2)
cc: FB | Logical Graphs • Laws of Form

Posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | Tagged Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | 12 Comments

Paradisaical Logic and the After Math • Comment 1

Posted on April 4, 2021 by Jon Awbrey

Re: Peter Cameron • Cultures, Tribes, or Just an Illusion?
Re: Peirce List • (1) (2) (3) (4) (5) (6)

One of those recurring themes — you might call it “The Power of Negative Thinking” — arose this time on the Peirce List and it took me back to a post I wrote nine Aprils ago and that took me even further back to the very doors I first walked through into the wonderland of logic à la Peirce.

I fixed the links broken by the ravages of time and the impings of web developers and I added more links to the original context of discussion. A partial transcript follows.

Paradisaical Logic and the After Math

Not too coincidentally with the mention of Peirce’s existential graphs, a tangent of discussion elsewhere brought to mind an old favorite passage from Peirce, where he is using his entitative graphs to expound the logic of relatives. Here is the observation I was led to make.

Paradisaical Logic

Negative operations (NOs), if not more important than positive operations (POs), are at least more powerful or generative, because the right NOs can generate all POs, but the reverse is not so.

Which brings us to Peirce’s amphecks, Nand and Nnor, either of which is a sole sufficient operator for all boolean operations.

In one of his developments of a graphical syntax for logic, that described in passing an application of the Neither-Nor operator, Peirce referred to the stage of reasoning before the encounter with falsehood as “paradisaical logic, because it represents the state of Man’s cognition before the Fall.”

Here’s a bit of what he wrote there —

C.S. Peirce • Relatives of Second Intention

Resources

cc: Cybernetics • Ontolog • Peirce List (1) (2) • Structural Modeling • Systems Science
cc: FB | Logical Graphs • Laws of Form

Animated Logical Graphs • 69

Posted on March 30, 2021 by Jon Awbrey

Re: Richard J. Lipton • The Art Of Math
Re: Animated Logical Graphs • (57) • (58) • (59) • (60) • (61) • (62) • (63) • (64) • (65) • (66)

“I know what you mean but I say it another way” — it’s a thing I find myself saying often enough, if only under my breath, to rate an acronym for it ☞ IKWYMBISIAW ☜ and not too coincidentally it’s a rubric of relevance to many situations in semiotics where sundry manners of speaking and thinking converge, more or less, on the same patch of pragmata.

We encountered just such a situation in our exploration of the duality between entitative and existential interpretations of logical graphs. The two interpretations afford distinct but equally adequate ways of reasoning about a shared objective domain. To cut our teeth on a simple but substantial example of an object domain, we picked the space of boolean functions or propositional forms on two variables. This brought us to the following Table, highlighting the sign relation $L \subseteq O \times S \times I$ involved in switching between existential and entitative interpretations of logical graphs.

$\text{Peirce Duality as Sign Relation}$

Column 1 shows the object domain $O$ as the set of 16 boolean functions on 2 variables.
Column 2 shows the sign domain $S$ as a representative set of logical graphs denoting the objects in $O$ according to the existential interpretation.
Column 3 shows the interpretant domain $I$ as the same set of logical graphs denoting the objects in $O$ according to the entitative interpretation.

Resources

cc: Cybernetics (1) (2) • Peirce (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14)
cc: Ontolog Forum (1) (2) • Structural Modeling (1) (2) • Systems Science (1) (2)
cc: FB | Logical Graphs • Laws of Form

Animated Logical Graphs • 68

Posted on March 29, 2021 by Jon Awbrey

Re: Animated Logical Graphs • (14) • (15) • (16) • (17) • (18) • (19) • (20) • (21)
Re: Ontolog Forum • Mauro Bertani

Dear Mauro,

Let’s take a another look at the Table we reached at the end of Episode 21.

I call it a Formal Operation Table — rather than, say, a Truth Table — because it describes the operation of mathematical forms preceding the stage of logical interpretation. I know the word formal tends to get overworked past the point of semantic fatigue but I can still hope to revive it a little. We’ll use other labels for Table entries at other times but I tried this time to mitigate interpretive bias by choosing a mix of senses from both Peirce and Spencer Brown.

Entering the stage of logical interpretation, we arrive at the following two options.

The entitative interpretation of $\texttt{(} a \texttt{,} b \texttt{)}$ produces the truth table for logical equality.

The existential interpretation of $\texttt{(} a \texttt{,} b \texttt{)}$ produces the truth table for logical inequality, also known as exclusive disjunction.

Resource

Futures Of Logical Graphs • Themes and Variations

Animated Logical Graphs • 67

Posted on March 27, 2021 by Jon Awbrey

Re: Animated Logical Graphs • (14) • (15) • (16) • (17) • (18) • (19) • (20)
Re: Differential Propositional Calculus • Discussion • (4) • (5) • (6)
Re: Laws of Form • Lyle Anderson
Re: Peirce List • Mauro Bertani

Dear Lyle,

Yes, the ability to work with functions as “first class citizens”, as we used to say, is one of the things making lambda calculus at the theoretical level and Lisp at the practical level so nice. All of which takes us straight into Curry-Howard-ville …

Dear Mauro,

That is the right ball park, functional calculi and all that. I haven’t been taking time out to mention all the players apart from Peirce and Spencer Brown — Boole, Frege, Schönfinkel, Curry, Howard, and others — because I’m still in the middle of tackling Helmut Raulien’s question about the link between cactus graphs and differential logic. At any rate I’ll be focused on that for a while longer.

Regards,

Jon

Differential Propositional Calculus • Discussion 6

Posted on March 22, 2021 by Jon Awbrey

Re: Oeis | Differential Propositional Calculus • Part 1 • Part 2 • Appendices
Re: Blog | Differential Propositional Calculus • Discussion • (3) • (4) • (5)

HR:

I think I like very much your Cactus Graphs. Meaning that I am in the process of understanding them, and finding it much better not to have to draw circles, but lines.
Less easy for me is the differential calculus. Where is the consistency between $\texttt{(} x \texttt{,} y \texttt{)}$ and $\texttt{(} x \texttt{,} y \texttt{,} z \texttt{)}?$ $\texttt{(} x \texttt{,} y \texttt{)}$ means that $x$ and $y$ are not equal and $\texttt{(} x \texttt{,} y \texttt{,} z \texttt{)}$ means that one of them is false. Unequality and truth/falsity for me are two concepts so different I cannot think them together or see a consistency between them.
What about $\texttt{(} w \texttt{,} x \texttt{,} y \texttt{,} z \texttt{)}?$

Dear Helmut,

Table 1 shows the cactus graphs, the corresponding cactus expressions in “traversal string” or plain text form, their logical meanings under the “existential interpretation”, and their translations into conventional notations for a number of common propositional forms. I’ll change variables to $\{ x, a, b, c \}$ instead of $\{ w, x, y, z \}$ at this point simply because I’ve already got a Table like that on hand.

As far as the consistency between $\texttt{(} a \texttt{,} b \texttt{)}$ and $\texttt{(} a \texttt{,} b \texttt{,} c \texttt{)}$ goes, that’s easy enough to see — if exactly one of two boolean variables is false then the two must have different values.

Out of time for today, so I’ll get to the rest of your questions next time.

Table 1. Syntax and Semantics of a Calculus for Propositional Logic

cc: Cybernetics • Laws of Form • Ontolog Forum • Peirce List (1) (2) (3)
cc: FB | Differential Logic • Structural Modeling • Systems Science

Posted in Amphecks, Boolean Functions, C.S. Peirce, Cactus Graphs, Category Theory, Change, Computational Complexity, Cybernetics, Differential Analytic Turing Automata, Differential Calculus, Differential Logic, Discrete Dynamics, Dynamical Systems, Equational Inference, Functional Logic, Gradient Descent, Graph Theory, Group Theory, Hologrammautomaton, Indicator Functions, Logic, Logical Graphs, Mathematical Models, Mathematics, Minimal Negation Operators, Painted Cacti, Peirce, Propositional Calculus, Propositional Equation Reasoning Systems, Time, Visualization | Tagged Amphecks, Boolean Functions, C.S. Peirce, Cactus Graphs, Category Theory, Change, Computational Complexity, Cybernetics, Differential Analytic Turing Automata, Differential Calculus, Differential Logic, Discrete Dynamics, Dynamical Systems, Equational Inference, Functional Logic, Gradient Descent, Graph Theory, Group Theory, Hologrammautomaton, Indicator Functions, Logic, Logical Graphs, Mathematical Models, Mathematics, Minimal Negation Operators, Painted Cacti, Peirce, Propositional Calculus, Propositional Equation Reasoning Systems, Time, Visualization | 8 Comments

Differential Propositional Calculus • Discussion 5

Posted on March 21, 2021 by Jon Awbrey

Re: Peirce List • Helmut Raulien
Re: Ontolog Forum • Mauro Bertani

HR:

I think I like very much your Cactus Graphs. Meaning that I am in the process of understanding them, and finding it much better not to have to draw circles, but lines.
Less easy for me is the differential calculus. Where is the consistency between $\texttt{(} x \texttt{,} y \texttt{)}$ and $\texttt{(} x \texttt{,} y \texttt{,} z \texttt{)}?$ $\texttt{(} x \texttt{,} y \texttt{)}$ means that $x$ and $y$ are not equal and $\texttt{(} x \texttt{,} y \texttt{,} z \texttt{)}$ means that one of them is false. Unequality and truth/falsity for me are two concepts so different I cannot think them together or see a consistency between them.
What about $\texttt{(} w \texttt{,} x \texttt{,} y \texttt{,} z \texttt{)}?$

MB:: So, if I want to transform a circle into a line I have to use a function $f : \mathbb{B}^n \to \mathbb{B}?$
This is the base of temporal logic? I’m using $f : \mathbb{N}^n \to \mathbb{N}.$

Dear Mauro,

If I understand what Helmut is saying about “circles” and “lines”, he is talking about the passage from forms of enclosure on plane sheets of paper — such as those used by Peirce and Spencer Brown — to their topological duals in the form of rooted trees. There is more discussion of this transformation at the following sites.

This is the first step in the process of converting planar maps to graph-theoretic data structures. Further transformations take us from trees to the more general class of cactus graphs, which implement a highly efficient family of logical primitives called minimal negation operators. These are described in the following article.

Minimal Negation Operators

cc: Cybernetics • Laws of Form • Ontolog Forum • Peirce List (1) (2) (3)
cc: FB | Differential Logic • Structural Modeling • Systems Science

Differential Propositional Calculus • Discussion 4

Posted on March 20, 2021 by Jon Awbrey

It is one of the rules of my system of general harmony, that the present is big with the future, and that he who sees all sees in that which is that which shall be.

Leibniz • Theodicy

Re: R.J. Lipton • Anti-Social Networks
Re: Lou Kauffman • Iterants, Imaginaries, Matrices
Re: Logical Cactus Graphs @ All Process, No Paradox • 6
Re: Differential Propositional Calculus • Discussion 3
Re: Peirce List • Helmut Raulien

HR:

I think I like very much your Cactus Graphs. Meaning that I am in the process of understanding them, and finding it much better not to have to draw circles, but lines.
Less easy for me is the differential calculus. Where is the consistency between $\texttt{(} x \texttt{,} y \texttt{)}$ and $\texttt{(} x \texttt{,} y \texttt{,} z \texttt{)}?$ $\texttt{(} x \texttt{,} y \texttt{)}$ means that $x$ and $y$ are not equal and $\texttt{(} x \texttt{,} y \texttt{,} z \texttt{)}$ means that one of them is false. Unequality and truth/falsity for me are two concepts so different I cannot think them together or see a consistency between them.
What about $\texttt{(} w \texttt{,} x \texttt{,} y \texttt{,} z \texttt{)}?$
Can you give a grammar, like, what does a comma mean, what do brackets mean, what does writing letters following each other with an empty space but no comma mean, and so on?
Same with Cactus Graphs, though I think, they might be self-explaining for me — everything is self-explaining, depending on intellectual capacity, but mine is limited.

Dear Helmut,

Many thanks for your detailed comments and questions. They help me see the places where more detailed explanation is needed. I added numbers to your points above for ease of reference and possible future reference in case I can’t get to them all in one pass.

I’m glad you found the cactus graphs to your liking. It was a critical transition for me when I passed from trees to cacti in my graphing and programming and it came about by recursively applying a trick of thought I learned from Peirce himself. These days I call it a “Meta-Peircean Move” to apply one of Peirce’s heuristics of choice or standard operating procedures to the state of development resulting from previous applications. All that makes for a longer story I made a start at telling in the following series of posts.

Animated Logical Graphs • (14) • (15) • (16) • (17) • (18) • (19) • (20) • (21) • (22) • (23) • (24) • (25) • (26) • (27)

Well, the clock in the hall struck time for lunch some time ago, so I think I’ll heed its call and continue later …

Regards,

Jon

cc: Cybernetics • Laws of Form • Ontolog Forum • Peirce List (1) (2) (3)
cc: FB | Differential Logic • Structural Modeling • Systems Science

All Process, No Paradox • 9

Posted on March 18, 2021 by Jon Awbrey

In the midst of this strife, whereat the halls of Ilúvatar shook and a tremor ran out into the silences yet unmoved, Ilúvatar arose a third time, and his face was terrible to behold. Then he raised up both his hands, and in one chord, deeper than the Abyss, higher than the Firmament, piercing as the light of the eye of Ilúvatar, the Music ceased.

Tolkien • Ainulindalë

Re: Objects, Models, Theories • (1) • (2) • (3)
Re: Peirce List • Helmut Raulien

Continuing my review of previous discussions concerned with various proposals to extend bivalent logic to encompass sundry dimensions of alterity, change, diversity, dynamics, imagination, indefinability, indeterminacy, information, interpretation, intuitionism, likelihood, mutability, probability, quantity, relativity, time, uncertainty, and so on.

For continuity’s sake I’m recycling my replies to a comment by Helmut Raulien on the Peirce List which raised a host of questions about Peirce’s categories, logic, and semiotics in the light of Spencer Brown’s Laws of Form.

Comment 1

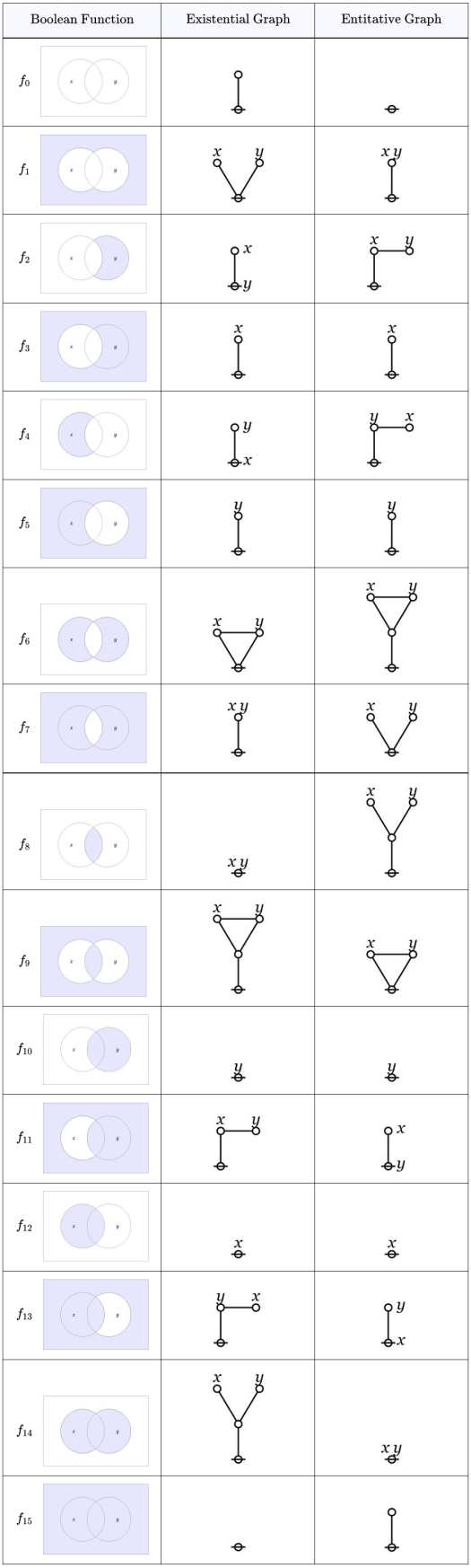
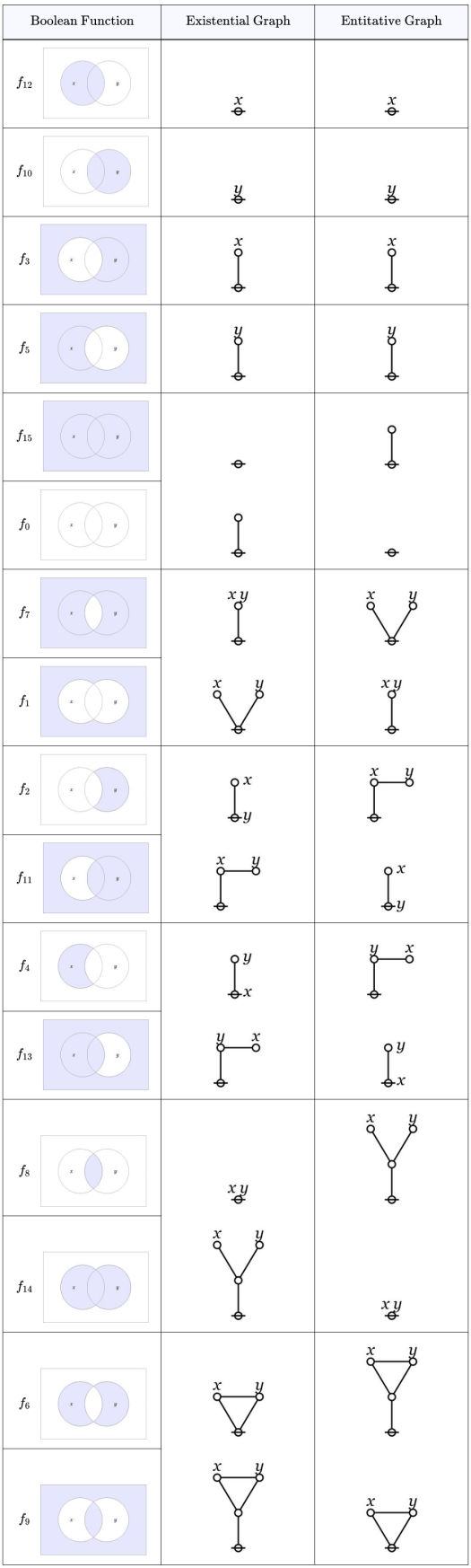
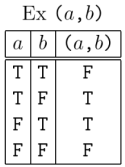
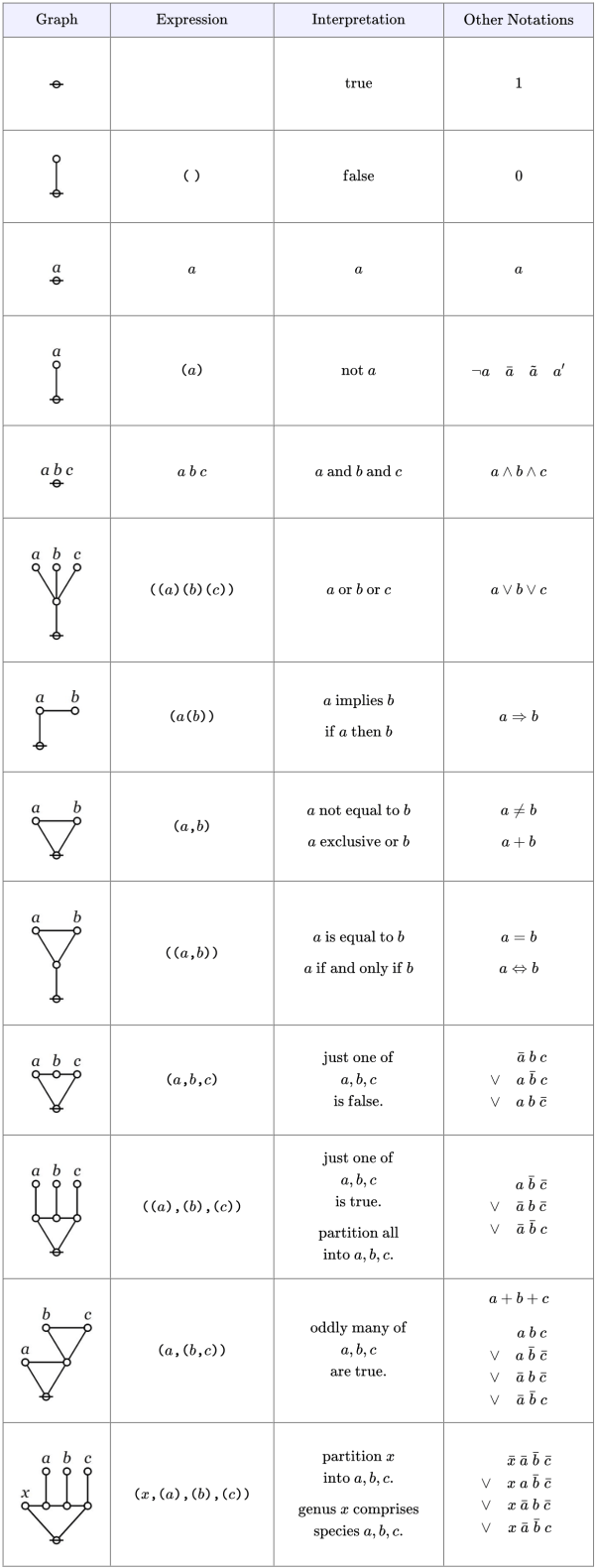
George Spencer Brown’s Laws of Form tends to be loved XOR hated by most folks, with few coming down in between. I ran across the book early in my undergrad years, shortly after encountering C.S. Peirce, so I recognized the way it revived Peirce’s logical graphs, emphasizing the entitative interpretation of the abstract formal calculus immanent in Peirce’s “Alpha” graphs. It took me a decade to gain a modicum of clarity about all that “imaginary truth value” and “re-entry” folderol. I’ll say some things about that later on.

Comment 2

I mulled the matter over for a fair spell of days and nights and decided it wouldn’t be good to jump into the middle of the muddle about re-entry and imaginary truth values right off the bat, that it would be better in the long run to get a solid grip on what is going on with the propositional level of Peirce’s logical graphs and how Spencer Brown’s elaborations can be seen to manifest the same spirit of reasoning, if they are read the right way. Toward that end I’ll append a list of resources to break the ice on this approach.

Resources

Logic Syllabus
Semeiotic, Semiotics
Precursors Of Category Theory
Logical Graphs • Introduction • Formal Development
Differential Propositional Calculus • Part 1 • Part 2

cc: Cybernetics • Laws of Form • Ontolog Forum • Peirce List
cc: FB | Cybernetics • Structural Modeling • Systems Science

Posted in Animata, C.S. Peirce, Category Theory, Cybernetics, Differential Logic, Laws of Form, Logic, Logical Graphs, Mathematics, Paradox, Peirce, Process, Semiotics, Spencer Brown, Systems Theory, Tertium Quid, Time, Tolkien | Tagged Animata, C.S. Peirce, Category Theory, Cybernetics, Differential Logic, Laws of Form, Logic, Logical Graphs, Mathematics, Paradox, Peirce, Process, Semiotics, Spencer Brown, Systems Theory, Tertium Quid, Time, Tolkien | 7 Comments

	Survey of Differenti… on Differential Logic • 9
	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…
	Differential Logic •… on Logic Syllabus
	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…
	Differential Logic •… on Logic Syllabus
	Survey of Differenti… on Differential Logic • 8
	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…

Inquiry Into Inquiry

Paradisaical Logic and the After Math • Comment 2

Resources

Animated Logical Graphs • 70

Resources

Paradisaical Logic and the After Math • Comment 1

Paradisaical Logic and the After Math

Paradisaical Logic

Resources

Animated Logical Graphs • 69

Resources

Animated Logical Graphs • 68

Resource

Animated Logical Graphs • 67

All Process, No Paradox • 9

Comment 1

Comment 2

Resources

Elsewhere

Blogroll

Follow Blog via Email

Recent Posts

Recent Comments

Archives

Blog Stats

Categories

Logic, Mathematics, Philosophy

Inquiry Driven Systems

Cybernetics

Differential Logic

Logical Graphs

Minimal Negation Operators

Peirce Matters

Relation Theory

Riffs & Rotes

Semeiotics

Theme One

Current Events

Fawkes News

Meta

Resources

Share this:

Resources

Share this:

Paradisaical Logic

Resources

Share this:

Resources

Share this:

Resource

Share this:

Share this:

Share this:

Share this:

Share this:

Resources

Share this:

Elsewhere

Blogroll

Follow Blog via Email

Recent Posts

Recent Comments

Archives

Blog Stats

Categories

Logic, Mathematics, Philosophy

Current Events

Meta