Differential Logic, Dynamic Systems, Tangent Functors • Discussion 4

Posted on December 17, 2018 by Jon Awbrey

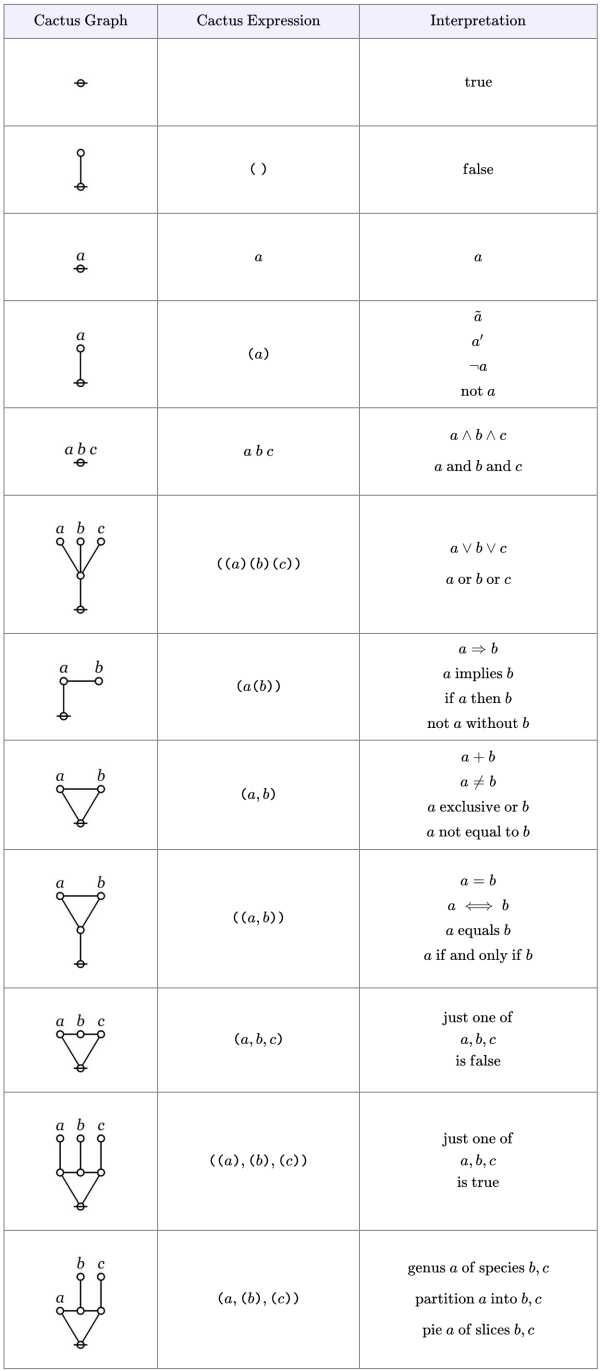
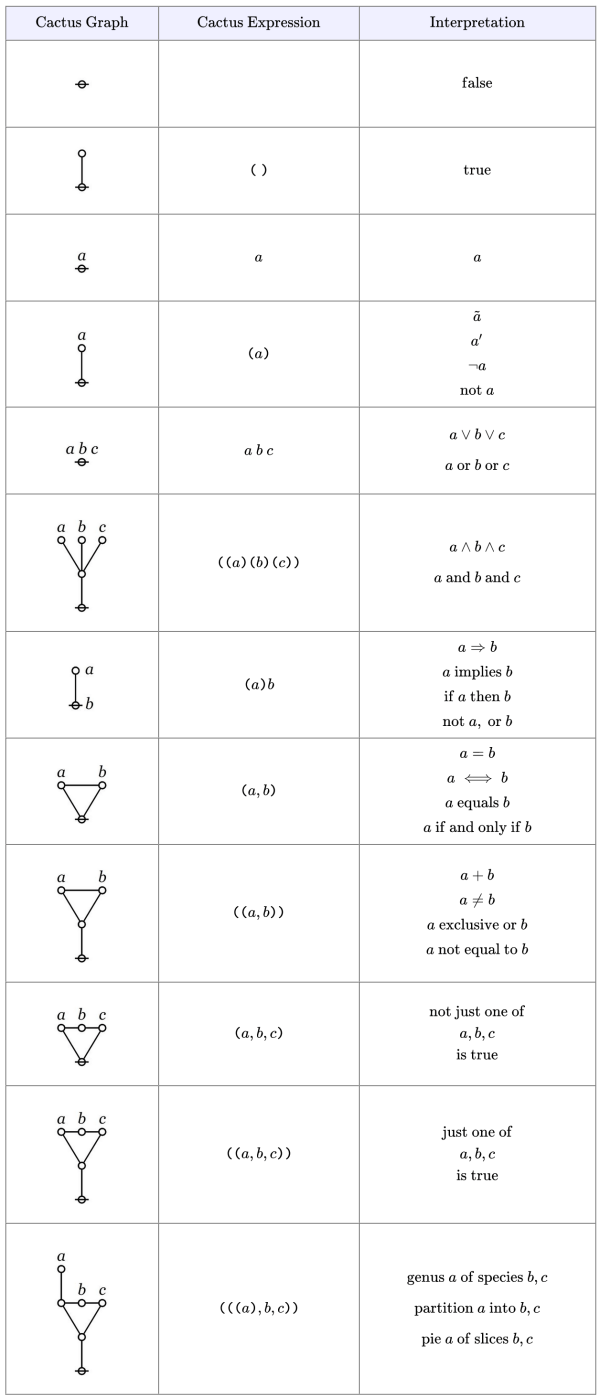
Re: Systems Science • LT

To clarify my previous remark about General Systems Theory, I wasn’t trying to define a whole field but merely to describe my experience in forums like these, where it took me a while to realize that when I use the word “system” a great many people are not thinking what I’m thinking when I use it.  The first thing in my mind is almost always a state space X and the possible trajectories of a representative point through it.  But a lot of people will be thinking of a “system”, like the word says, as a collection of parts “standing together”.  Naturally I’d like to reach the point of discussing such things, it’s just that it takes me a while, and considerable analysis of X, to get there.

It goes without saying this has to do with the boundaries of my own experience and the emphases of my teachers and other influencers in systems, the early ones taking their ground in Ashby, Wiener, and the MIT school, the later ones stressing optimal control and learning organizations, but mostly it has to do with my current objectives and the species of intelligent systems, Inquiry Driven Systems, I want to understand and help to build.

Resources

cc: Structural Modeling • Ontolog Forum • Laws of Form • Cybernetics

Posted in Amphecks, Boolean Functions, C.S. Peirce, Cactus Graphs, Category Theory, Cybernetics, Differential Analytic Turing Automata, Differential Calculus, Differential Logic, Discrete Dynamical Systems, Dynamical Systems, Graph Theory, Hill Climbing, Hologrammautomaton, Information Theory, Inquiry Driven Systems, Intelligent Systems, Knowledge Representation, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Painted Cacti, Peirce, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Systems, Visualization | Tagged , , , , , , , , , , , , , , , , , , , , , , , , , , , , , | 12 Comments

Differential Logic, Dynamic Systems, Tangent Functors • Discussion 3

Posted on December 12, 2018 by Jon Awbrey

Re: Systems Science • (1) • (2) • (3)

Various discussions in various places bring back to mind this thread from early this fall, prompting me to make a try at continuing it.  Here’s a series of blog posts where I kept track of a few points along the way:

Another thing to keep in mind here is the difference between General Systems Theory, following on Bertalanffy et al., and what is known as Dynamical Systems Theory (DST) or Mathematical Systems Theory (MST).  GST spends a lot of time studying part-whole hierarchies while DST/MST deals with the state space of a system and the possible trajectories of the system through it.

Category theory is especially useful in the latter application, abstracting or generalizing as it does the concepts of mathematical objects, functions, and transformations.

For my part I have come to take the DST/MST approach as more fundamental since it starts with fewer assumptions about the anatomy or architecture of the as-yet hypothetical agent, making it one of the first and continuing tasks of the agent to discover its own boundaries, potentials, and structures.

Resources

cc: Systems Science • Structural Modeling • Ontolog Forum • Laws of Form • Cybernetics

Posted in Amphecks, Boolean Functions, C.S. Peirce, Cactus Graphs, Category Theory, Cybernetics, Differential Analytic Turing Automata, Differential Calculus, Differential Logic, Discrete Dynamical Systems, Dynamical Systems, Graph Theory, Hill Climbing, Hologrammautomaton, Information Theory, Inquiry Driven Systems, Intelligent Systems, Knowledge Representation, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Painted Cacti, Peirce, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Systems, Visualization | Tagged , , , , , , , , , , , , , , , , , , , , , , , , , , , , , | 9 Comments

Semiotics, Semiosis, Sign Relations • 3

Posted on December 11, 2018 by Jon Awbrey

For ease of reference, here are two variants of Peirce’s 1902 definition of a sign, which he gives in the process of defining logic.

Selections from C.S. Peirce, “Carnegie Application” (1902)

No. 12.  On the Definition of Logic

Logic will here be defined as formal semiotic.  A definition of a sign will be given which no more refers to human thought than does the definition of a line as the place which a particle occupies, part by part, during a lapse of time.  Namely, a sign is something, A, which brings something, B, its interpretant sign determined or created by it, into the same sort of correspondence with something, C, its object, as that in which itself stands to C.  It is from this definition, together with a definition of “formal”, that I deduce mathematically the principles of logic.  I also make a historical review of all the definitions and conceptions of logic, and show, not merely that my definition is no novelty, but that my non-psychological conception of logic has virtually been quite generally held, though not generally recognized.  (NEM 4, 20–21).

No. 12.  On the Definition of Logic [Earlier Draft]

Logic is formal semiotic.  A sign is something, A, which brings something, B, its interpretant sign, determined or created by it, into the same sort of correspondence (or a lower implied sort) with something, C, its object, as that in which itself stands to C.  This definition no more involves any reference to human thought than does the definition of a line as the place within which a particle lies during a lapse of time.  It is from this definition that I deduce the principles of logic by mathematical reasoning, and by mathematical reasoning that, I aver, will support criticism of Weierstrassian severity, and that is perfectly evident.  The word “formal” in the definition is also defined.  (NEM 4, 54).

Reference

  • Peirce, C.S. (1902), “Parts of Carnegie Application” (L 75), in Carolyn Eisele (ed., 1976), The New Elements of Mathematics by Charles S. Peirce, vol. 4, 13–73.  Online.

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science

Posted in C.S. Peirce, Category Theory, Logic, Relation Theory, Semiosis, Semiotics, Sign Relations, Triadic Relations | Tagged , , , , , , , | 24 Comments

Semiotics, Semiosis, Sign Relations • 2

Posted on December 10, 2018 by Jon Awbrey

Here are links to more complete discussions of semiotics.

The approach described here develops from what I regard as the core definition of triadic sign relations, one explicit enough to support a consequential theory of signs.  Peirce gives that definition in the process of defining logic itself, as detailed in the following texts.

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science

Posted in C.S. Peirce, Category Theory, Logic, Relation Theory, Semiosis, Semiotics, Sign Relations, Triadic Relations | Tagged , , , , , , , | 24 Comments

Semiotics, Semiosis, Sign Relations • 1

Posted on December 9, 2018 by Jon Awbrey

A first mention of semiotics (and cybersemiotics) in a discussion group gave me a chance to begin a fresh introduction to the subject.  I thought it might be useful to share that here.

Here’s the intro to Semiotics I wrote for Wikipedia many moons ago.  There wasn’t much left of it the last time I looked there but I had foresightfully saved several copies elsewhere.

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science

Posted in C.S. Peirce, Category Theory, Logic, Relation Theory, Semiosis, Semiotics, Sign Relations, Triadic Relations | Tagged , , , , , , , | 25 Comments

Theme One • A Program Of Inquiry 17

Posted on December 7, 2018 by Jon Awbrey

The move is all over but the unpacking, and the time looks ripe to pick up the following thread from last spring.  Here, by way of a quick refresher, are a few Tables from earlier discussions.

Theme One • A Program Of Inquiry 11

Existential Interpretation

Table 1 illustrates the existential interpretation of cactus graphs and cactus expressions by providing English translations for a few of the most basic and commonly occurring forms.

\text{Table 1. Existential Interpretation}
Existential Interpretation

Entitative Interpretation

Table 2 illustrates the entitative interpretation of cactus graphs and cactus expressions by providing English translations for a few of the most basic and commonly occurring forms.

\text{Table 2. Entitative Interpretation}
Entitative Interpretation

Theme One Program • Appendices

  • Table C displays the existential and entitative interpretations in parallel columns.

Differential Logic and Dynamic Systems • Appendices

cc: Ontolog Forum • Systems Science

Posted in Algorithms, Animata, Artificial Intelligence, Boolean Functions, C.S. Peirce, Cactus Graphs, Cognition, Computation, Constraint Satisfaction Problems, Data Structures, Differential Logic, Equational Inference, Formal Languages, Graph Theory, Inquiry Driven Systems, Laws of Form, Learning Theory, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Painted Cacti, Peirce, Propositional Calculus, Semiotics, Spencer Brown, Visualization | Tagged , , , , , , , , , , , , , , , , , , , , , , , , , , | 7 Comments

Pragmatic Semiotic Information • Discussion 11

Posted on December 2, 2018 by Jon Awbrey

Re: Ontolog Forum • Ferenc Kovacs
Re: Anja-Karina Pahl • Contradiction and Analogy as the Basis for Inventive Thinking

One of the insights coming out of Peirce’s logical work is the fact that negative operations are more powerful than positive operations in the sense that negative operations can generate all possible operations while positive operations by themselves do not suffice.  This is epitomized by his discovery of the amphecks as sole sufficient operators for propositional logic.

The propositional logic algorithm I wrote for my Theme One Program turns this principle to good effect in two ways:

  • The graph-theoretic syntax is based on a graph-theoretic operator, a type of controlled negation called the minimal negation operator, that generalizes Peirce’s graph-theoretic operator for negation.
  • It turns out that recognizing contradictions quickly makes for a high degree of efficiency in finding the “models” or satisfying interpretations of a propositional formula.

Relations of contradiction are also critical in statistical inference, but I’ll need to save that for another day.

Resources

  • Ampheck • (1) • (2)
  • Minimal Negation Operator • (1) • (2)

cc: Systems Science • Structural Modeling

Posted in Abduction, Aristotle, C.S. Peirce, Comprehension, Deduction, Definition, Determination, Extension, Hypothesis, Induction, Inference, Information, Information = Comprehension × Extension, Inquiry, Intension, Intention, Logic, Logic of Science, Mathematics, Measurement, Observation, Peirce, Perception, Phenomenology, Physics, Pragmatic Semiotic Information, Pragmatism, Probability, Quantum Mechanics, Scientific Method, Semiotics, Sign Relations | Tagged , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , | 9 Comments

Pragmatic Semiotic Information • Discussion 10

Posted on November 20, 2018 by Jon Awbrey

Re: Ontolog Forum

Artem Kaznatcheev posted an interesting discussion on his blog under the title “Models as Maps and Maps as Interfaces” that I saw as fitting under this head.  A reader of Peirce may recognize critical insights of pragmatic thought cropping up toward the end of his analysis, prompting me to add the following comment:

Map and “mirror of nature” metaphors take us a good distance in understanding how creatures represent their worlds to themselves and others.  But from a pragmatic semiotic point of view we can see how these metaphors lock us into iconic forms of representation, overstretching dyadic relations, and thus falling short of the full power of triadic symbolic relations that support practical interaction with the world.

cc: Systems Science • Structural Modeling

Posted in Abduction, Aristotle, C.S. Peirce, Comprehension, Deduction, Definition, Determination, Extension, Hypothesis, Induction, Inference, Information, Information = Comprehension × Extension, Inquiry, Intension, Intention, Logic, Logic of Science, Mathematics, Measurement, Observation, Peirce, Perception, Phenomenology, Physics, Pragmatic Semiotic Information, Pragmatism, Probability, Quantum Mechanics, Scientific Method, Semiotics, Sign Relations | Tagged , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , | 8 Comments

Indicator Functions • Discussion 1

Posted on October 10, 2018 by Jon Awbrey

Peter Smith, on his Logic Matters blog, asks the question, “What Is A Predicate?”, and considers a number of answers.

There are of course other possible answers, and one I learned quite early on, arising very naturally in applying mathematical logic to what were generally known as “AI problems”, like perception and pattern recognition, and the one I found increasingly useful as I took up the reflective stance on symbolic computation afforded by Peirce’s pragmatic semiotics, may be described as follows:

In many applications a predicate is a function from a universe of discourse X to a binary value in \mathbb{B} = \{0, 1\}, that is, a characteristic function or indicator function f : X \to \mathbb{B}, and f^{-1}(1), the fiber of 1 under f, is the set of elements denoted or indicated by the predicate.  That is the semantics, anyway.  As far as syntax goes, there are many formal languages whose syntactic expressions serve as names for those functions and nominally speaking one may call those names predicates.

cc: Ontolog Forum • Systems Science • Structural Modeling

Posted in Boole, Boolean Functions, C.S. Peirce, Category Theory, Indication, Indicator Functions, Logic, Mathematics, Peirce, Propositional Calculus, Propositional Equation Reasoning Systems, Set Theory, Venn Diagrams | Tagged , , , , , , , , , , , , | 1 Comment

{ Information = Comprehension × Extension } • Comment 8

Posted on October 8, 2018 by Jon Awbrey

So what is all this fuss about the relation between inquiry and signs, as analyzed in Peirce’s theories of their structure and function and synthesized in his theory of information?

The best way I’ve found to see where the problem lies is to run through a series of concrete examples of the sort Peirce used to illustrate his notions of information, inquiry, and signs, examples just complex enough to show the interplay of main ideas.

There is an enlightening set of examples in Peirce’s early lectures on the Logic of Science.  Here is the blog post I wrote to set up their discussion:

Another angle from which to approach the incidence of signs and inquiry is by way of C.S. Peirce’s “laws of information” and the corresponding theory of information he developed from the time of his lectures on the “Logic of Science” at Harvard University (1865) and the Lowell Institute (1866).

When it comes to the supposed reciprocity between extensions and intensions, Peirce, of course, has another idea, and I would say a better idea, partly because it forms the occasion for him to bring in his new-fangled notion of “information” to mediate the otherwise static dualism between the other two.  The development of this novel idea brings Peirce to enunciate the formula:

\mathrm{Information} = \mathrm{Comprehension} \times \mathrm{Extension}

But comprehending what in the world that might mean is a much longer story, the end of which your present teller has yet to reach.  So, this time around, I will take up the story near the end of the beginning of Peirce’s own telling of it, for no better reason than that’s where I myself initially came in, or, at least, where it all started making any kind of sense to me.  And from this point we will find it easy enough to flash both backward and forward, to and fro, as the occasions arise for doing so.

Reference

  • Peirce, C.S. (1866), “The Logic of Science, or, Induction and Hypothesis”, Lowell Lectures of 1866, pp. 357–504 in Writings of Charles S. Peirce : A Chronological Edition, Volume 1, 1857–1866, Peirce Edition Project, Indiana University Press, Bloomington, IN, 1982.

Resources

cc: Ontolog Forum • Structural Modeling • Systems Science

Posted in Abduction, Belief Fixation, C.S. Peirce, Comprehension, Deduction, Extension, Hypothesis, Icon Index Symbol, Induction, Inference, Information, Information = Comprehension × Extension, Inquiry, Intension, Logic, Logic of Science, Peirce, Peirce's Categories, Pragmatism, Scientific Method, Semiotic Information, Semiotics, Sign Relations | Tagged , , , , , , , , , , , , , , , , , , , , , , | 8 Comments