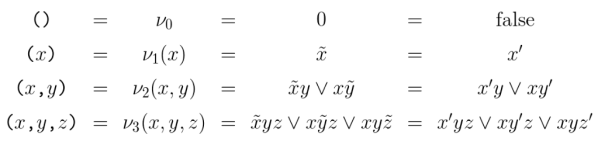Note. I’m including a more detailed definition of minimal negation operators in terms of conventional logical operations largely because readers of particular tastes have asked for it in the past. But it can easily be skipped until one has a felt need for it. Skimmed lightly, though, it can serve to illustrate a major theme in logic and mathematics, namely, the Relativity of Complexity or the Relativity of Primitivity to the basis we have chosen for constructing our conceptual superstructures.
⁂ ⁂ ⁂
Defining minimal negation operators over a more conventional basis is next in order of exposition, if not necessarily in order of every reader’s reading. For what it’s worth and against the day when it may be needed, here is a definition of minimal negations in terms of 
 and
and 
Formal Definition
To express the general form of 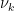 in terms of familiar operations, it helps to introduce an intermediary concept.
in terms of familiar operations, it helps to introduce an intermediary concept.
Definition. Let the function 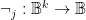 be defined for each integer
be defined for each integer  in the interval
in the interval ![[1, k]](https://s0.wp.com/latex.php?latex=%5B1%2C+k%5D&bg=ffffff&fg=000000&s=0&c=20201002) by the following equation.
by the following equation.

Then  is defined by the following equation.
is defined by the following equation.

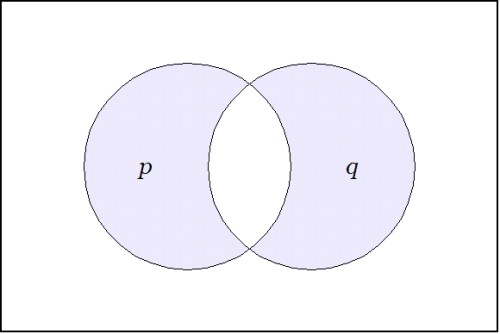
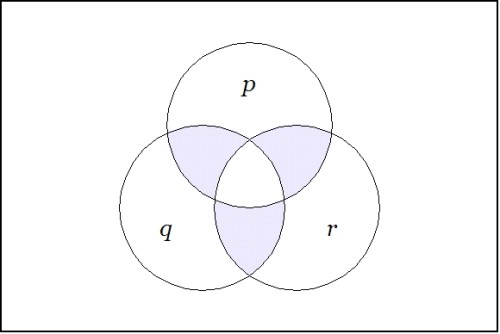
We may take the boolean product  or the logical conjunction
or the logical conjunction  to indicate the point
to indicate the point 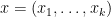 in the space
in the space  in which case the minimal negation
in which case the minimal negation  indicates the set of points in
indicates the set of points in 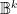 which differ from
which differ from  in exactly one coordinate. This makes
in exactly one coordinate. This makes  a discrete functional analogue of a point-omitted neighborhood in ordinary real analysis, more precisely, a point-omitted distance-one neighborhood. Viewed in that light the minimal negation operator can be recognized as a differential construction, an observation opening a very wide field.
a discrete functional analogue of a point-omitted neighborhood in ordinary real analysis, more precisely, a point-omitted distance-one neighborhood. Viewed in that light the minimal negation operator can be recognized as a differential construction, an observation opening a very wide field.
The remainder of this discussion proceeds on the algebraic convention making the plus sign  and the summation symbol
and the summation symbol  both refer to addition mod 2. Unless otherwise noted, the boolean domain
both refer to addition mod 2. Unless otherwise noted, the boolean domain  is interpreted for logic in such a way that
is interpreted for logic in such a way that  and
and  This has the following consequences.
This has the following consequences.
-
The operation
 is a function equivalent to the exclusive disjunction of
is a function equivalent to the exclusive disjunction of  and
and  while its fiber of
while its fiber of  is the relation of inequality between
is the relation of inequality between  and
and 
-
The operation
 maps the bit sequence
maps the bit sequence 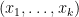 to its parity.
to its parity.
The following properties of the minimal negation operators  may be noted.
may be noted.
-
The function
 is the same as that associated with the operation
is the same as that associated with the operation  and the relation
and the relation 
-
In contrast,
 is not identical to
is not identical to 
-
More generally, the function
 for
for  is not identical to the boolean sum
is not identical to the boolean sum 
-
The inclusive disjunctions indicated for the
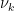 of more than one argument may be replaced with exclusive disjunctions without affecting the meaning since the terms in disjunction are already disjoint.
of more than one argument may be replaced with exclusive disjunctions without affecting the meaning since the terms in disjunction are already disjoint.
Resources
cc: Cybernetics • Ontolog Forum • Peirce List • Structural Modeling • Systems Science
cc: FB | Minimal Negation Operators • Laws of Form