Inquiry Into Inquiry

A statement that implies both and is called a false statement, and anyone can prove anything at all from a false statement, as we all too frequently observe on the political front these days.

There is however a reasonable way of handling boundaries, for instance, as illustrated by the circumference of a region in a venn diagram, and that is by means of differential logic.  I’ve been tortoising my way toward the goal line of explaining all that, and it’s going a bit slow, but there’s a gentle introduction at the other end of the link below, if you wish to achilles ahead.

• Differential Propositional Calculus • Part 1

cc: Cybernetics • Laws of Form • Ontolog • Peirce • Structural Modeling • Systems Science

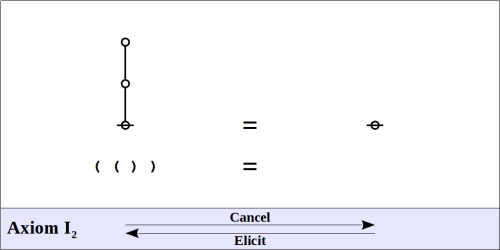
The formal system of logical graphs is defined by a foursome of formal equations, called initials when regarded purely formally, in abstraction from potential interpretations, and called axioms when interpreted as logical equivalences.  There are two arithmetic initials and two algebraic initials, as shown below.

Arithmetic Initials

Algebraic Initials

Spencer Brown uses a different formal equation for his first algebraic initial — where I use    he uses    For the moment, let’s refer to my as 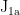and his as and use that notation to examine the relationship between the two systems.

It is easy to see that the two systems are equivalent, since we have the following proof of by way of 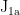and

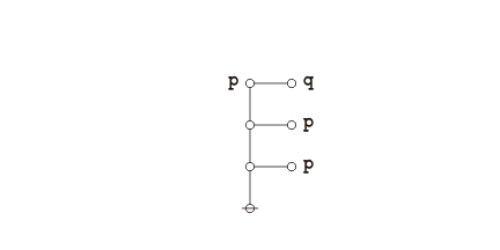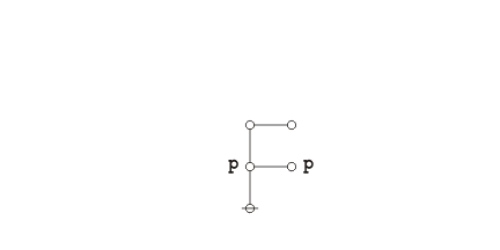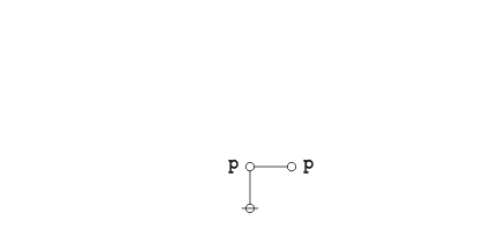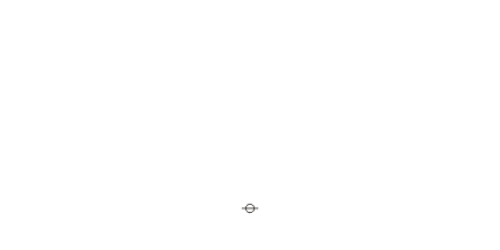
 a   a
 o---o
 |
 @

 =======J1a {delete}

 o---o
 |
 @

 =======I2  {cancel}

 @

 =======QED J1b

In choosing between systems I am less concerned with small differences in the lengths of proofs than I am with other factors.  It is difficult for me to remember all the reasons for decisions I made forty or fifty years ago — as a general rule, Peirce’s way of looking at the relation between mathematics and logic has long been a big influence on my thinking and the other main impact is accountable to the nuts and bolts requirements of computational representation.

But looking at the choice with present eyes, I think I continue to prefer the system over the alternative simply for the fact it treats two different types of operation separately, namely, changes in graphical structure versus changes in the placement of variables.

cc: Cybernetics • Laws of Form • Ontolog • Peirce • Structural Modeling • Systems Science

Here are blog and wiki versions of an article I wrote on Peirce’s Law, an axiom or theorem (depending on your choice of logical basis) which distinguishes classical from intuitionistic propositional calculus.  Aside from its pivotal logical status it affords a nice illustration of several important features of logical graphs in the style of Peirce and Spencer Brown.

• Peirce’s Law • This Blog • OEIS Wiki • InterSciWiki • MyWikiBiz • Wikiversity

Resource

• Propositions As Types Analogy

cc: Cybernetics • Laws of Form • Ontolog • Peirce • Structural Modeling • Systems Science

Two things impacting my studies of Peirce and Spencer Brown over the years were my parallel studies in mathematics and computer science.  In the overlap between those areas came courses in logic, mathematical linguistics, and the theory of formal languages, grammars, and automata.

My intellectual wanderings over a nine‑year undergraduate career would take me through a cycle of majors from math and physics, to communication, psychology, philosophy, and a cross‑cultural liberal arts program, then back to grad school in mathematics.

The puzzles Peirce and Spencer Brown beset my brain with were a big part of what drove me back to math, since I could see I had no chance of resolving them without learning a lot more algebra, logic, and topology than I had learned till then.

Resources

• Prospects for Inquiry Driven Systems • Bibliography
• Mathematical Notes • Philosophical Notes • Source Materials

cc: Cybernetics • Laws of Form • Ontolog • Peirce • Structural Modeling • Systems Science

Re: Laws of Form

There are a number of “difficulties at the beginning” that arise here.  I’ve been trying to get to the point where I can respond to James Bowery’s initial comments and also to questions about the relation between Spencer Brown’s imaginary logical values and the development of differential logic.

The larger issue I see at this point has to do with the relationship between the algebra and the arithmetic of logical graphs.  Peirce came right up to the threshold of discovering that relationship several times in his later work on existential graphs but never quite pushed it through to full realization.  It was left to Spencer Brown to bring it to light.

The relationship between Primary Arithmetic and Primary Algebra is discussed in the following article.

• Logical Graphs
• Primary Arithmetic as Semiotic System
• Primary Algebra as Pattern Calculus

The other issue has to do with my using a different than Spencer Brown.  I believe I even called it in the early days but eventually lost the prime as time went by.  As far as I can remember, it initially had to do with negotiating between the systems of C.S. Peirce and Spencer Brown but I think I stuck with the variant because it sorts the types of change — modifying structure and moving variables — into different bins.

• Image Files
• This Blog • I₁ • I₂ • J₁ • J₂
• Oeis Wiki • I₁ • I₂ • J₁ • J₂

See also the discussions at the following locations.

• Logical Graphs • Formal Development
• Propositional Equation Reasoning Systems

cc: Cybernetics • Laws of Form • Ontolog • Peirce • Structural Modeling • Systems Science

Re: Laws of Form

I’m making an effort to present this material in a more gradual and logical order than I’ve ever managed to do before.  There are issues about the relationship between episodic and semantic memory that are giving me trouble as I try to remember how I came to look at things the way I do … but never mind that now.  I’ll eventually get around to explaining the forces that drove me to generalize the forms of logical graphs from trees to cacti, as graph theorists call them, and how that made the transition to differential logic so much easier than it would have been otherwise, but I think it would be better now to begin at the beginning with the common core of forms introduced by CSP and GSB.

Here’s a couple of articles I wrote for that purpose:

• Logical Graphs
• Propositional Equation Reasoning Systems

There are versions of those articles at several other places on the web which may be better formatted or more convenient for discussion:

• Logical Graphs (Wikiversity)
• Logical Graphs (Inquiry Blog) • (1) • (2)

One big issue arising at the beginning is the question of “duality”.  Both C.S. Peirce and Spencer Brown understood they were dealing with a very abstract calculus, one which could be interpreted for the purposes of ordinary propositional logic in two different ways.  Peirce called the two different ways of interpreting the abstract graphs his entitative and existential graphs.  He started out with a system of graphs he opted to interpret in the entitative manner but switched over to the existential choice as he developed his logical graphs beyond the purely propositional level.  Spencer Brown elected to emphasize the entitative reading in his main exposition but he was very clear in the terminology he used that the forms and transformations themselves are independent of their interpretations.

Table 1 at either of the locations linked below has columns for the graph-theoretic forms and the parenthesis-string forms of several basic expressions, reading them under the existential interpretation.

• Table 1. Syntax and Semantics of a Calculus for Propositional Logic • (a) • (b)

The Tables linked below serve to compare the existential and entitative interpretations of logical graphs by providing translations into familiar notations and English paraphrases for a few of the most basic and commonly occurring forms.

• Table A. Existential Interpretation
• Table B. Entitative Interpretation
• Table C. Dualing Interpretations

cc: Cybernetics • Laws of Form • Ontolog • Peirce • Structural Modeling • Systems Science

It’s almost 50 years now since I first encountered the volumes of Peirce’s Collected Papers in the math library at Michigan State, and shortly afterwards a friend called my attention to the entry for Spencer Brown’s Laws of Form in the Whole Earth Catalog and I sent off for it right away.  I would spend the next decade just beginning to figure out what either one of them was talking about in the matter of logical graphs and I would spend another decade after that developing a program, first in Lisp and then in Pascal, converting graph-theoretic data structures formed on their ideas to good purpose in the mechanics of its propositional reasoning engine.  I thought it might contribute to a number of ongoing discussions if I could articulate what I think I learned from that experience.

cc: Cybernetics • Laws of Form • Ontolog • Peirce • Structural Modeling • Systems Science