Sign Relations, Triadic Relations, Relation Theory • Discussion 4

Posted on December 31, 2020 by Jon Awbrey

Dyadic Versus Dichotomic

Re: Previous Post
Re: Cybernetics • Cliff Joslyn

Dear Cliff,

Many thanks for your thoughtful reply.  I copied a transcript to my blog to take up first thing next year.  Here’s hoping we all have a better one!

Regards,

Jon

CJ:
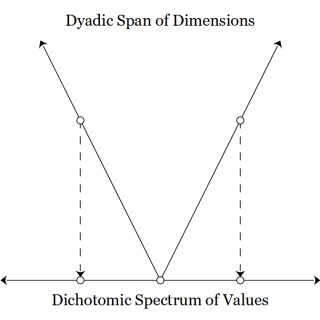
I think what you have is sound, and can be described in a number of ways.  In years past in seeking ways to both qualify and quantify variety in systems I characterized this distinction as between “dimensional variety” and “cardinal variety”.  Thankfully, this seems straightforward from a mathematical perspective, namely in a standard relational system S = \times_{i=1}^k X_i, where the X_i are dimensions (something that can vary), typically cast as sets, so that \times here is Cartesian product.  Here k is the dimensional variety (number of dimensions, k-adicity), while n_i = |X_i| is the cardinal variety (cardinality of dimension i, n_i-tomicity (n_i-tonicity, actually?)).  One might think of the two most classic examples:
  • Multiadic diatom/nic:  Maximal (finite) dimensionality, minimal non-trivial cardinality:  The bit string (b_1, b_2, \ldots, b_k) where there are k Boolean dimensions X_i = \{ 0, 1 \}.  One can imagine k \to \infty, an infinite bit string, even moreso.
  • Diadic infini-omic:  Minimal non-trivial dimensionality, maximal cardinality:  The Cartesian plane \mathbb{R}^2, where there are 2 real dimensions.
There’s another quantity you didn’t mention, which is the overall “variety” or size of the system, so \prod_{i=1}^k n_i, which is itself a well-formed expression (only) if there are a finite number of finite dimensions.

Resources

cc: Cybernetics • Ontolog • Peirce List (1) (2) • Structural Modeling • Systems Science

This entry was posted in C.S. Peirce, Icon Index Symbol, Information, Inquiry Driven Systems, Logic, Logic of Relatives, Mathematics, Peirce, Pragmatism, Relation Theory, Semiosis, Semiotics, Sign Relations, Triadic Relations, Triadicity, Visualization and tagged , , , , , , , , , , , , , , , . Bookmark the permalink.