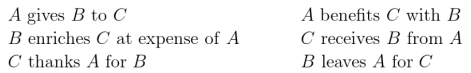Re: Peirce List • Robert Marty (quoted)
- RM:
- I persist in the idea that in your six combinations [O, S, I] only one is relevant for semiotics, the others being out of the field […] On the projections, there is also matter for discussion … but to discuss well one must reserve a rather large agenda … I thus wait for your reply dealing with semiosis to resume a debate well-centered on the essential …
Dear Robert,
Returning to our discussion of -place relations and the
conversions they enjoy under the action of the symmetric group
permuting their places, it’s been a while so I’ll extract the substance of my last reply and continue from there.
We had been contemplating Peirce’s variations on a theme of giving as presented in the section of the Sign Relation article titled “Six Ways of Looking at a Sign Relation”. That section begins as follows.
we make no distinction in the ordinary logic of relations between the subject nominative, the direct object, and the indirect object. We say that the proposition has three logical subjects. We regard it as a mere affair of English grammar that there are six ways of expressing this:
These six sentences express one and the same indivisible phenomenon.
(C.S. Peirce, “The Categories Defended”, MS 308 (1903), EP 2, 170–171).
I called attention to the moral Peirce draws.
- “These six sentences express one and the same indivisible phenomenon.”
With that one statement Peirce draws the clearest possible line of demarcation between affairs of grammar and affairs of logic, mathematics, and phenomena.
The same lesson applies to any relation whose places are not in general reserved for fixed types of entities, in particular, it applies to triadic sign relations. As we say, “objects, signs, and interpretants are roles not essences”.
Regards,
Jon
cc: Category Theory • Cybernetics (1) (2)
cc: Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Semeiotics • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)