Logical Graphs, Iconicity, Interpretation • 2

Posted on October 4, 2021 by Jon Awbrey

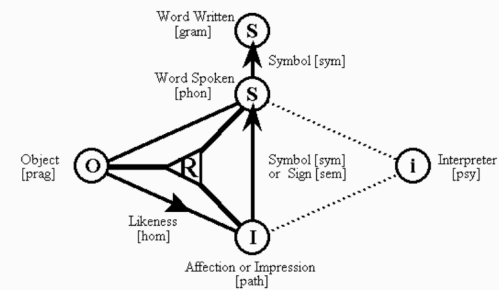
In the first place there are likenesses or copies — such as statues, pictures, emblems, hieroglyphics, and the like.  Such representations stand for their objects only so far as they have an actual resemblance to them — that is agree with them in some characters. The peculiarity of such representations is that they do not determine their objects — they stand for anything more or less;  for they stand for whatever they resemble and they resemble everything more or less.

The second kind of representations are such as are set up by a convention of men or a decree of God.  Such are tallies, proper names, &c.  The peculiarity of these conventional signs is that they represent no character of their objects.  Likenesses denote nothing in particular;  conventional signs connote nothing in particular.

The third and last kind of representations are symbols or general representations.  They connote attributes and so connote them as to determine what they denote.  To this class belong all words and all conceptions.  Most combinations of words are also symbols.  A proposition, an argument, even a whole book may be, and should be, a single symbol.

C.S. Peirce (1866), Lowell Lecture 7, CE 1, 467–468

The Table in the previous post can now be sorted to bring out the “family resemblances”, likenesses, or symmetries among logical graphs and the boolean functions they denote, where the “orbits” or similarity classes are determined by the dual interpretation of logical graphs.  Performing the sort produces the following Table.  As we have seen in previous discussions, there are 10 orbits in all, 4 orbits of 1 point each and 6 orbits of 2 points each.

\text{Boolean Functions and Logical Graphs on Two Variables} \stackrel{_\bullet}{} \text{Orbit Order}

Boolean Functions and Logical Graphs on Two Variables

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Logical Graphs • Laws of Form • Peirce List

Posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | Tagged , , , , , , , , , , , , , , , , , , , , , , , , , | 8 Comments

Logical Graphs, Iconicity, Interpretation • 1

Posted on October 3, 2021 by Jon Awbrey

If exegesis raised a hermeneutic problem, that is, a problem of interpretation, it is because every reading of a text always takes place within a community, a tradition, or a living current of thought, all of which display presuppositions and exigencies — regardless of how closely a reading may be tied to the quid, to “that in view of which” the text was written.

Paul Ricoeur • The Conflict of Interpretations

If a picture is worth a thousand words, here’s my 48,000 words worth on the recurring question of logical graphs, their iconicity, and their interpretation, at least as concerns Peirce’s alpha graphs interpreted for propositional logic.  A few more actual words, literally speaking, may be called for.  I’ll return to that anon.

Referring to the Table —

  • Column 1 shows a conventional name f_{i} and a venn diagram for each of the sixteen boolean functions on two variables.
  • Column 2 shows the logical graph canonically representing the boolean function in Column 1 under the entitative interpretation.  This is the interpretation C.S. Peirce used in his earlier work on entitative graphs and the one Spencer Brown used in his book Laws of Form.
  • Column 3 shows the logical graph canonically representing the boolean function in Column 1 under the existential interpretation.  This is the interpretation C.S. Peirce used in his later work on existential graphs.

\text{Boolean Functions and Logical Graphs on Two Variables}

Boolean Functions and Logical Graphs on Two Variables

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Logical Graphs • Laws of Form • Peirce List

Posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | Tagged , , , , , , , , , , , , , , , , , , , , , , , , , | 9 Comments

Minimal Negation Operators • Discussion 2

Posted on October 2, 2021 by Jon Awbrey

Re: Minimal Negation Operators • (1) • (2) • (3) • (4)
Re: Peirce List (1) (2) (3) • Jerry Chandler

JC:
As a chemist, CSP often inscended hyle terminology into his logical corpse as he sought to extend the 15–17th century historical usages of the meaning of the concept of a “term”.

One particularity of chemical synthesis is the absence of the “negative” operators on the chemical elements.  Each element is a logical constant in the language of chemistry and hence can not be negated.  Yet, in the notation for chemistry it is necessary to assert and signify the absence of a chemical unit in a logical product.  This could be referred to as a minimal negation in a logically consistent semantics of a chemical syntax.

I have no information, either positive or negative, of the meaning Jon intends to infer logically with his usage of this non-standard semantics.  However, this semantics is obviously useful in attempting to give a logical semantics for the well‑established semiosis of hyle.

Dear Jerry,

I’ve been spending a lot of time lately thinking about how I first got into all the things I’ve gotten into over the years.  The thing that surprised me the most was how much of my life I’ve been immersed in raw data despite my best efforts to rise above it in flights of theory and just plain fancy.  The honors chemistry course I took my first year in college was pretty advanced — we “hit the ground running” as my Dad used to say from his paratroop days — moving from covalent bonding theory the first term to molecular orbital theory the second.

It was there I first encountered the triple interaction of theory, experiment, and electronic computation.  Aside from the routine programs we ran to analyze our data, drawing least squares lines through experimental scatterplots and all that, I began my first attempts to compute with symbolic forms, trying to get Fortran to place the electron dots around and between chemical symbols in various molecular combinations.  Mostly I learned to dislike Fortran — wrong tool for the job, I guess — and it would be years before I woke to Lisp.

At any rate, let me beg off on chemical logic or logical chemistry.  My experiences in that borderland are more a tale of fits and starts than anything conclusive and reconstructing the details would take a search through the darker corners of my basement archives.

The matter of “non-standard semantics”, however, is a timely and topical subject to address, one it would dispel a mass of obscurities about the link between logic and semiotics to clarify as much as we can.

To begin, we may pose the question as follows.

  • In what way does a propositional calculus based on minimal negation operators deviate from standard semantics?

I will take that up next time, perhaps under a different heading.

Regards,

Jon

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Minimal Negation Operators • Laws of Form • Peirce List (1) (2) (3)

Posted in Amphecks, Animata, Boolean Functions, C.S. Peirce, Cactus Graphs, Differential Logic, Functional Logic, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Painted Cacti, Peirce, Propositional Calculus, Propositional Equation Reasoning Systems, Semiotics, Venn Diagrams, Visualization | Tagged , , , , , , , , , , , , , , , , , , , | 6 Comments

Minimal Negation Operators • Discussion 1

Posted on September 30, 2021 by Jon Awbrey

Re: Minimal Negation Operators • (1) • (2) • (3) • (4)
Re: Peirce List (1) (2) • Imran Makani

IM:
In his first post on this thread Jon clearly says that [minimal negation operators] were developed from Peirce’s alpha graphs for propositional calculus and that he has even outlined the history of this early development in a previous series of posts.

Dear Imran,

Welcome to the List and heartfelt thanks for your appreciation of my contribution to it.  I’m just a person who goes to sleep every night and wakes up every morning with sundry issues in Peirce’s work in the forefront of his mind.  It has been that way — no doubt with less persistence at first, there were other demands and diversions in the early days — since I chanced on Peirce’s work my first year in college and right up to the present time when my inquiries into the consequences of his work literally pervade my dreams and days.

If you’ll excuse my anecdotage, it took me nine years to complete my Bachelor of Arts — demands and diversions were abundant — matriculating first in Math and Physics, taking a break in Communication Arts where I tilted with Aristotle, at long last mustering out in a cross-cultural-cultivating radical-liberal arts college with a concentration I created myself in “Mathematical And Philosophical Method”.  The cornerstone of that first year and the capstone of my senior thesis, “Complications of the Simplest Mathematics”, compass the dark night and the dawn’s light of my Peirce Decade One.

Well, I’ve run out of time for now …
I’ll continue this memoir tomorrow …

Regards,

Jon

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Minimal Negation Operators • Laws of Form • Peirce List (1) (2)

Posted in Amphecks, Animata, Boolean Functions, C.S. Peirce, Cactus Graphs, Differential Logic, Functional Logic, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Painted Cacti, Peirce, Propositional Calculus, Propositional Equation Reasoning Systems, Semiotics, Venn Diagrams, Visualization | Tagged , , , , , , , , , , , , , , , , , , , | 6 Comments

Semiotics, Semiosis, Sign Relations • Discussion 18

Posted on September 28, 2021 by Jon Awbrey

Re: FB | Medieval Logic • Edward Buckner (1) (2)

Edward Buckner raised a few questions about the sign relations implicit in Aristotle’s treatise “On Interpretation”, prompting the following thoughts on my part.

On Pragmata

The object of a sign is any object of discussion or thought.  It is relational not ontological.  This is the beginning of pragmatic semiotics.

On Homoiomata

The likeness theory of reference has the same problem as the correspondence theory of truth, namely, the concepts of likeness and correspondence used in those theories both refer to dyadic relations and dyadic relations are not adequate to the task of accounting for the complex of activities composing the intellect, for example, inquiry, learning, reasoning, speech, thought, in short, Information Development/Exchange Activities.

In actuality, Aristotle comes closer to recognizing the triadic relation of Objects, Signs, and Ideas than the majority of later writers before Peirce.  Here is the figure Susan Awbrey and I cut in our first hack at the matter.

The Sign Relation in Aristotle

Figure 1.  The Sign Relation in Aristotle

Resources

cc: Category Theory • Cybernetics (1) (2) • Ontolog Forum • Peirce List (1) (2) (3) (4)
cc: FB | Semeiotics • Laws of Form • Structural Modeling • Systems Science

Posted in C.S. Peirce, Category Theory, Logic, Relation Theory, Semiosis, Semiotics, Sign Relations, Triadic Relations | Tagged , , , , , , , | 8 Comments

Relations & Their Relatives • Discussion 23

Posted on September 21, 2021 by Jon Awbrey

Re: Ontolog Forum • Roberto Rovetto • Alex Shkotin

Having lost my concentration to another round of home reconstruction disruption, let me loop back to the texts from Roberto and Alex which drew me into this discussion last week.

RR:

What’s your view on:

When to create a greater-than-binary relation rather than a binary relation?

Consider:  You want to represent some information, statement, or knowledge, without necessarily being forced to limit to binary relations.  A common example is when wanting to reference time.  And “between” is greater than binary.  What are other pieces of knowledge that you’d want assert a ternary, or greater than binary relation to capture it accurately?

Do you have any rules of thumb for knowing when to assert n-ary relations greater than binary?

AS:
Let me underline an important point:  first of all, we have found in nature and society one or another relation and ask how many members each example of this relation can have?  i.e. arity is a feature of relation itself.  So […] we come here to the logic of relations and its discovery.  For me, examples of relations of different arity from one or another domain would be great.

I will take up k-adic or k-ary relations from a mathematical perspective and I will treat them from the standpoint of one whose “customers” over his actually getting paid years were academic, education, health, and research science units or investigators engaged in gathering data by means of experiments, empirical studies, or survey instruments and analyzing those data according to the protocols of qualitative observation methods or quantitative statistical hypothesis testing, all toward the purpose of discovering reproducible facts about their research domains and subject populations.

A sidelong but critically necessary reflection on the research scene comes from the Peircean perspective on scientific inquiry, in which triadic relations and especially triadic sign relations are paramount.  I will develop Peirce’s pragmatic, semiotic, information-theoretic viewpoint in tandem with the treatment of relation theory.

Resources

cc: Category Theory • Cybernetics • Ontolog • Structural Modeling • Systems Science
cc: FB | Relation Theory • Laws of Form • Peirce List (1) (2) (3)

Posted in C.S. Peirce, Category Theory, Control, Cybernetics, Dyadic Relations, Information, Inquiry, Logic, Logic of Relatives, Mathematics, Peirce, Relation Theory, Semiosis, Semiotics, Sign Relations, Systems Theory, Triadic Relations | Tagged , , , , , , , , , , , , , , , , | 8 Comments

Susan Awbrey • I Looked Up

Posted on September 20, 2021 by Jon Awbrey

I Looked Up

I looked up and I was old
      The loose, wrinkled skin
      The lines that leave their traces
I looked up and I was old
      The scars of former illness written there
I looked up and I was old
      I ask my body why it has forsaken me
      It said it has been there through it all
I looked up and I was old
      But my spirit is the same
      Youth but a breath away
I looked up and I was one
      With ancient earth and new born robin
I looked up and my gaze rose
      Beyond my mollusk shell to the infinity that is now

❧ Susan Awbrey
     September 19, 2021

Posted in Guest Post, Susan Awbrey | Tagged , | Leave a comment

Differential Logic • Discussion 15

Posted on September 18, 2021 by Jon Awbrey

Re: Differential Logic • Comment 7
Re: Laws of Form • Lyle Anderson

LA:
Differentials and partial differentials over the real numbers work because one can pick two real numbers that are arbitrarily close to one another.  The difference between any two real numbers can be made as small as desired.  If you have a real function of a real variable then you characterize the change in the function’s real value as the value of the argument changes.  This can be represented as the tangent to the curve representing the function at a given point.

In the Boolean domain there are only two values and they are always one step, unity, apart.  There is nothing to differentiate.  There is no variation in the spacing of the arguments or the function values.  There are no curves in the Boolean domain.  There is nothing to differentiate.

Dear Lyle,

My last post is really just a note-to-self reminding me to get back to work on differential logic, my memory being jogged by a number of posts on the Azimuth Blog.  But if I could nudge a few people to reflect on what the logical analogue of differential calculus ought to look like, that would be a plus.

The short answer to your objection is we don’t need limits in discrete spaces.  We follow the example of the finite difference calculus, using logical analogues of the enlargement operator \mathrm{E} and the difference operator \mathrm{D}.

A differential is a locally linear approximation to a function, that is, a linear function which approximates another function at a point.  In boolean spaces, we know what the functions are, we know what the linear functions are, and all we need is a notion of approximation to define differentials.  Yes, there are numerous tricky bits to work out in boolean spaces, but I worked those out in the array of expositions at many different levels of abstraction and detail to which I have linked before, as again below.

Recent Discussions

Resources

cc: Category Theory • Cybernetics • Ontolog • Structural Modeling • Systems Science
cc: FB | Differential Logic • Laws of Form

Posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Category Theory, Change, Cybernetics, Differential Analytic Turing Automata, Differential Calculus, Differential Logic, Discrete Dynamics, Equational Inference, Frankl Conjecture, Functional Logic, Gradient Descent, Graph Theory, Hologrammautomaton, Indicator Functions, Inquiry Driven Systems, Leibniz, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Painted Cacti, Peirce, Propositional Calculus, Surveys, Time, Topology, Visualization, Zeroth Order Logic | Tagged , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , | 8 Comments

Differential Logic • Comment 7

Posted on September 17, 2021 by Jon Awbrey

Re: John Baez • Cyclic Identity for Partial Derivatives • Maxwell’s Relations (1) (2) (3)

Much fun can be had by trying to do differentials and partial differentials over the boolean domain \mathbb{B} = \{ 0, 1 \} instead of the reals \mathbb{R}.

I took a first whack at it in the following project report.

Resources

cc: Category Theory • Cybernetics • Ontolog • Structural Modeling • Systems Science
cc: FB | Differential Logic • Laws of Form

Posted in Adaptive Systems, Amphecks, Belief Systems, Boole, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Cybernetics, Differential Logic, Discrete Dynamics, Fixation of Belief, Gradient Descent, Graph Theory, Hill Climbing, Hologrammautomaton, Inquiry, Inquiry Driven Systems, Laws of Form, Leibniz, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Optimization, Painted Cacti, Peirce, Propositional Calculus, Spencer Brown | Tagged , , , , , , , , , , , , , , , , , , , , , , , , , , , , | Comments Off on Differential Logic • Comment 7

Relations & Their Relatives • Discussion 22

Posted on September 16, 2021 by Jon Awbrey

Re: Ontolog Forum • Roberto Rovetto (1) (2)

RR:

What’s your view on:

When to create a greater-than-binary relation rather than a binary relation?

Consider:  You want to represent some information, statement, or knowledge, without necessarily being forced to limit to binary relations.  A common example is when wanting to reference time.  And “between” is greater than binary.  What are other pieces of knowledge that you’d want assert a ternary, or greater than binary relation to capture it accurately?

Do you have any rules of thumb for knowing when to assert n-ary relations greater than binary?

Dear Roberto,

Let me return to your original question and give it better attention.

You have probably noticed you got a wide variety of answers coming from a diversity of conceptual frameworks and philosophical paradigms.  It gradually dawned on me some years ago these differences are most likely matters of taste about which all dispute is futile, however much we go ahead and do it anyway.  So I’ll just say what I’ve found works best in my particular applications of interest, namely, applying relational logic to mathematics and research sciences.

To avoid the kinds of culture clashes I remember from the Standard Upper Ontology Lists and other ancestors of this Forum at the turn of the millennium, I’ll develop the rest of this line of inquiry on the thread for Relations and Their Relatives.

Regards,

Jon

cc: Category Theory • Cybernetics • Ontolog • Structural Modeling • Systems Science
cc: FB | Relation Theory • Laws of Form • Peirce List (1) (2) (3)

Posted in C.S. Peirce, Category Theory, Control, Cybernetics, Dyadic Relations, Information, Inquiry, Logic, Logic of Relatives, Mathematics, Peirce, Relation Theory, Semiosis, Semiotics, Sign Relations, Systems Theory, Triadic Relations | Tagged , , , , , , , , , , , , , , , , | 9 Comments