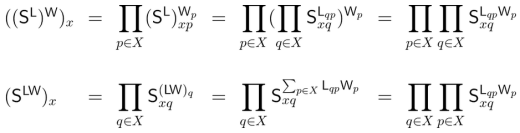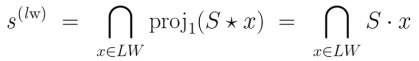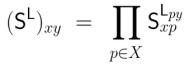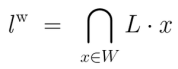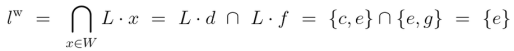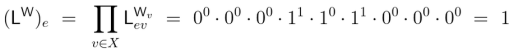Let us make a few preliminary observations about the operation of logical involution which Peirce introduces in the following words.
In ordinary arithmetic the involution 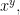 or the exponentiation of
or the exponentiation of  to the power
to the power  is the repeated application of the multiplier
is the repeated application of the multiplier  for as many times as there are ones making up the exponent
for as many times as there are ones making up the exponent 
In analogous fashion, the logical involution 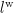 is the repeated application of the term
is the repeated application of the term  for as many times as there are individuals under the term
for as many times as there are individuals under the term 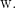 On Peirce’s interpretive rules, the repeated applications of the base term
On Peirce’s interpretive rules, the repeated applications of the base term  are distributed across the individuals of the exponent term
are distributed across the individuals of the exponent term 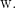 In particular, the base term
In particular, the base term  is not applied successively in the manner that would give something on the order of “a lover of a lover of … a lover of a woman”.
is not applied successively in the manner that would give something on the order of “a lover of a lover of … a lover of a woman”.
By way of example, suppose a universe of discourse numbers among its elements just three women,  In Peirce’s notation the fact may be written as follows.
In Peirce’s notation the fact may be written as follows.

In that case the following equation would hold.

The equation says a lover of every woman in the aggregate 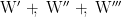 is a lover of
is a lover of 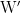 that is a lover of
that is a lover of  that is a lover of
that is a lover of  In other words, a lover of every woman in the universe at hand is a lover of
In other words, a lover of every woman in the universe at hand is a lover of 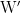 and a lover of
and a lover of  and a lover of
and a lover of 
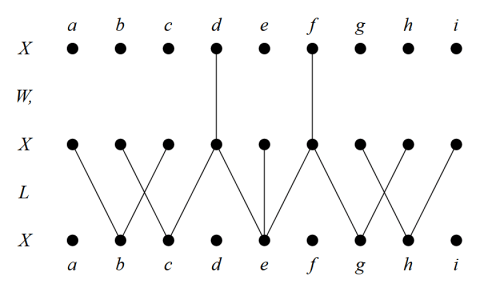
The denotation of the term 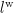 is a subset of
is a subset of  which may be obtained by the following procedure. For each flag of the form
which may be obtained by the following procedure. For each flag of the form 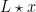 with
with 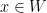 collect the subset
collect the subset  of elements which appear as the first components of the pairs in
of elements which appear as the first components of the pairs in 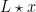 and then take the intersection of all those subsets. Putting it all together, we have the following equation.
and then take the intersection of all those subsets. Putting it all together, we have the following equation.

It is instructive to examine the matrix representation of 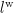 at this point, not the least because it effectively dispels the mystery of the name involution. First, we make the following observation. To say
at this point, not the least because it effectively dispels the mystery of the name involution. First, we make the following observation. To say  is a lover of every woman is to say
is a lover of every woman is to say  loves
loves  if
if  is a woman. That can be rendered in symbols as follows.
is a woman. That can be rendered in symbols as follows.

Reading the formula 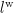 as “
as “ loves
loves  if
if  is a woman” highlights the operation of converse implication inherent in it, and this in turn reveals the analogy between implication and involution which accounts for the aptness of the latter name.
is a woman” highlights the operation of converse implication inherent in it, and this in turn reveals the analogy between implication and involution which accounts for the aptness of the latter name.
The operations defined by the formulas 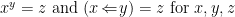 in the boolean domain
in the boolean domain  are tabulated as follows.
are tabulated as follows.

It is clear the two operations are isomorphic, being effectively the same operation of type 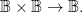 All that remains is to see how operations like these on values in
All that remains is to see how operations like these on values in 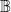 induce the corresponding operations on sets and terms.
induce the corresponding operations on sets and terms.
The term 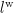 determines a selection of individuals from the universe of discourse
determines a selection of individuals from the universe of discourse  which may be computed via the corresponding operation on coefficient matrices. If the terms
which may be computed via the corresponding operation on coefficient matrices. If the terms  and
and  are represented by the matrices
are represented by the matrices  and
and 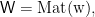 respectively, then the operation on terms which produces the term
respectively, then the operation on terms which produces the term 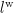 must be represented by a corresponding operation on matrices,
must be represented by a corresponding operation on matrices,  which produces the matrix
which produces the matrix  In short, the involution operation on matrices must be defined in such a way that the following equation holds.
In short, the involution operation on matrices must be defined in such a way that the following equation holds.

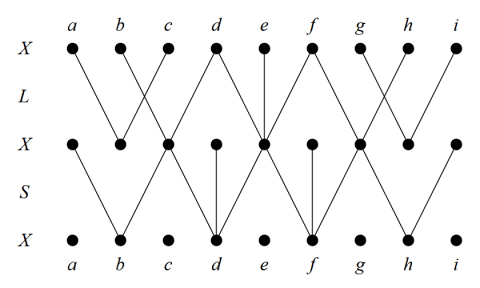
The fact that 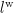 denotes individuals in a subset of
denotes individuals in a subset of  tells us its matrix representation
tells us its matrix representation  is a 1‑dimensional array of coefficients in
is a 1‑dimensional array of coefficients in 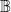 indexed by the elements of
indexed by the elements of  The value of the matrix
The value of the matrix  at the index
at the index  in
in  is written
is written 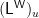 and computed as follows.
and computed as follows.

Resources
cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)