Peirce’s 1870 “Logic of Relatives” • Comment 11.23

Posted on June 5, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 11.23

Peirce’s description of logical conjunction and conditional probability via the logic of relatives and the mathematics of relations is critical to understanding the relationship between logic and measurement, in effect, the qualitative and quantitative aspects of inquiry.  To root that connection firmly in mind, I will try to sum up as succinctly as possible, in more current notation, the lesson we ought to take away from Peirce’s last “number of” example, since I know the account I have given so far may appear to have wandered widely.

NOF 4.3

So if men are just as apt to be black as things in general,

[\mathrm{m,}][\mathrm{b}] ~=~ [\mathrm{m,}\mathrm{b}],

where the difference between [\mathrm{m}] and [\mathrm{m,}] must not be overlooked.

(Peirce, CP 3.76)

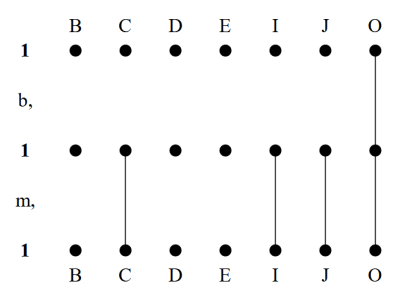
Viewed in different lights the formula [\mathrm{m,}\mathrm{b}] = [\mathrm{m,}][\mathrm{b}] presents itself as an aimed arrow, fair sampling, or statistical independence condition.  The concept of independence was illustrated in the previous installment by means of a case where independence fails.  The details of that counterexample are summarized below.

Othello Product M,B,
\text{Figure 54. Bigraph Product}~ M,B,

The condition that “men are just as apt to be black as things in general” is expressed in terms of conditional probabilities as \mathrm{P}(\mathrm{b}|\mathrm{m}) = \mathrm{P}(\mathrm{b}), which means that the probability of the event \mathrm{b} given the event \mathrm{m} is equal to the unconditional probability of the event \mathrm{b}.

In the Othello example it is enough to observe that \mathrm{P}(\mathrm{b}|\mathrm{m}) = \tfrac{1}{4} while \mathrm{P}(\mathrm{b}) = \tfrac{1}{7} in order to recognize the bias or dependency of the sampling map.

The reduction of a conditional probability to an absolute probability, as \mathrm{P}(A|Z) = \mathrm{P}(A), is one of the ways we come to recognize the condition of independence, \mathrm{P}(AZ) = \mathrm{P}(A)P(Z), via the definition of conditional probability, \mathrm{P}(A|Z) = \displaystyle{\mathrm{P}(AZ) \over \mathrm{P}(Z)}.

By way of recalling the derivation, the definition of conditional probability plus the independence condition yields the following sequence of equations.

\mathrm{P}(A|Z) = \displaystyle{\mathrm{P}(AZ) \over P(Z)} = \displaystyle{\mathrm{P}(A)\mathrm{P}(Z) \over \mathrm{P}(Z)} = \mathrm{P}(A).

As Hamlet discovered, there’s a lot to be learned from turning a crank.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form (1) (2) • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 11.22

Posted on June 4, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 11.22

Let’s look at that last example from a different angle.

NOF 4.3

So if men are just as apt to be black as things in general,

[\mathrm{m,}][\mathrm{b}] ~=~ [\mathrm{m,}\mathrm{b}],

where the difference between [\mathrm{m}] and [\mathrm{m,}] must not be overlooked.

(Peirce, CP 3.76)

Viewed in various lights the formula [\mathrm{m,}\mathrm{b}] = [\mathrm{m,}][\mathrm{b}] presents itself as an aimed arrow, fair sampling, or stochastic independence condition.

Peirce’s example assumes a universe of things in general encompassing the denotations of the absolute terms \mathrm{m} = \text{man} and \mathrm{b} = \text{black}.  That allows us to illustrate the case in relief, by returning to our earlier staging of Othello and examining the premiss that “men are just as apt to be black as things in general” within the frame of that empirical if fictional universe of discourse.

We have the following data.

\begin{array}{*{15}{l}} \mathrm{b} & = & \mathrm{O} \\[6pt] \mathrm{m} & = & \mathrm{C} & +\!\!, & \mathrm{I} & +\!\!, & \mathrm{J} & +\!\!, & \mathrm{O} \\[6pt] \mathbf{1} & = & \mathrm{B} & +\!\!, & \mathrm{C} & +\!\!, & \mathrm{D} & +\!\!, & \mathrm{E} & +\!\!, & \mathrm{I} & +\!\!, & \mathrm{J} & +\!\!, & \mathrm{O} \\[12pt] \mathrm{b,} & = & \mathrm{O\!:\!O} \\[6pt] \mathrm{m,} & = & \mathrm{C\!:\!C} & +\!\!, & \mathrm{I\!:\!I} & +\!\!, & \mathrm{J\!:\!J} & +\!\!, & \mathrm{O\!:\!O} \\[6pt] \mathbf{1,} & = & \mathrm{B\!:\!B} & +\!\!, & \mathrm{C\!:\!C} & +\!\!, & \mathrm{D\!:\!D} & +\!\!, & \mathrm{E\!:\!E} & +\!\!, & \mathrm{I\!:\!I} & +\!\!, & \mathrm{J\!:\!J} & +\!\!, & \mathrm{O\!:\!O} \end{array}

The fair sampling condition amounts to saying men are just as likely to be black as things in general are likely to be black.  In other words, men are a fair sample of things in general with respect to the predicate of being black.

On that condition the following equation holds.

[\mathrm{m,}\mathrm{b}] ~=~ [\mathrm{m,}][\mathrm{b}].

Assuming [\mathrm{b}] is not zero, the next equation follows.

[\mathrm{m,}] ~=~ \displaystyle{[\mathrm{m,}\mathrm{b}] \over [\mathrm{b}]}.

As before, it is convenient to represent the absolute term \mathrm{b} = \text{black} by means of the corresponding idempotent term \mathrm{b,} = \text{black that is}\,\underline{~~~~}. 

Let is next consider the bigraph for the following relational product.

\mathrm{m,}\mathrm{b} ~=~ \text{man that is black}.

We may represent that in the following equivalent form.

\mathrm{m,}\mathrm{b,} ~=~ \text{man that is black that is}\,\underline{~~~~}.

Othello Product M,B,
\text{Figure 53. Bigraph Product}~ M,B,

The facts of the matter in the Othello case are such that the following formula holds.

\mathrm{m,}\mathrm{b} ~=~ \mathrm{b}.

And that in turn is equivalent to each of the following statements.

\begin{matrix} m \land b = b \\[6pt] \mathrm{b} \implies \mathrm{m} \\[6pt] \mathrm{b} ~-\!\!\!< \mathrm{m} \end{matrix}

Those last implications puncture any notion of statistical independence for \mathrm{b} and \mathrm{m} in the universe of discourse at hand but it will repay us to explore the details of the case a little further.  Putting all the general formulas and particular facts together, we arrive at the following summation of the situation in the Othello case.

If the fair sampling condition were true, it would have the following consequence.

\displaystyle [\mathrm{m,}] ~=~ {[\mathrm{m,}\mathrm{b}] \over [\mathrm{b}]} ~=~ {[\mathrm{b}] \over [\mathrm{b}]} ~=~ \mathfrak{1}.

On the contrary, we have the following fact.

\displaystyle [\mathrm{m,}] ~=~ {[\mathrm{m,}\mathbf{1}] \over [\mathbf{1}]} ~=~ {[\mathrm{m}] \over [\mathbf{1}]} ~=~ {4 \over 7}.

In sum, it is not the case in the Othello example that “men are just as apt to be black as things in general”.

Expressed in terms of probabilities:

\mathrm{P}(\mathrm{m}) = \displaystyle{4 \over 7}   and   \mathrm{P}(\mathrm{b}) = \displaystyle{1 \over 7}.

If these were independent terms, we would have:

\mathrm{P}(\mathrm{m}\mathrm{b}) = \displaystyle{4 \over 49}.

In point of fact, however, we have:

\mathrm{P}(\mathrm{m}\mathrm{b}) = \mathrm{P}(\mathrm{b}) = \displaystyle{1 \over 7}.

Another way to see it is to observe that:

\mathrm{P}(\mathrm{b}|\mathrm{m}) = \displaystyle{1 \over 4}   while   \mathrm{P}(\mathrm{b}) = \displaystyle{1 \over 7}.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form (1) (2) • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 11 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 11.21

Posted on June 2, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 11.21

One more example and one more general observation and we’ll be caught up with our homework on Peirce’s “number of” function.

NOF 4.3

So if men are just as apt to be black as things in general,

[\mathrm{m,}][\mathrm{b}] ~=~ [\mathrm{m,}\mathrm{b}],

where the difference between [\mathrm{m}] and [\mathrm{m,}] must not be overlooked.

(Peirce, CP 3.76)

The protasis, men are just as apt to be black as things in general, is elliptic in structure and presents us with a potential ambiguity.  If we had no further clue to its meaning, it might be read as either one of the following statements.

  1. Men are just as apt to be black as things in general are apt to be black.
  2. Men are just as apt to be black as men are apt to be things in general.

The second interpretation, if grammatical, is pointless to state, since it equates a proper contingency with an absolute certainty.  So I think it is safe to assume the following paraphrase of what Peirce intends.

  • Men are just as likely to be black as things in general are likely to be black.

Stated in terms of conditional probability, we have the following equation.

\mathrm{P}(\mathrm{b}|\mathrm{m}) ~=~ \mathrm{P}(\mathrm{b}).

From the definition of conditional probability:

\mathrm{P}(\mathrm{b}|\mathrm{m}) ~=~ \displaystyle{\mathrm{P}(\mathrm{b}\mathrm{m}) \over \mathrm{P}(\mathrm{m})}.

Equivalently:

\mathrm{P}(\mathrm{b}\mathrm{m}) ~=~ \mathrm{P}(\mathrm{b}|\mathrm{m})\mathrm{P}(\mathrm{m}).

Taking everything together, we have the following result.

\mathrm{P}(\mathrm{b}\mathrm{m}) ~=~ \mathrm{P}(\mathrm{b}|\mathrm{m})\mathrm{P}(\mathrm{m}) ~=~ \mathrm{P}(\mathrm{b})\mathrm{P}(\mathrm{m}).

That, of course, is the definition of independent events, as applied to the event of being Black and the event of being a Man.  We may take that as the most likely reading of Peirce’s statement about frequencies:

[\mathrm{m,}\mathrm{b}] ~=~ [\mathrm{m,}][\mathrm{b}].

The terms of that equation can be normalized to produce the corresponding statement about probabilities.

\mathrm{P}(\mathrm{m}\mathrm{b}) ~=~ \mathrm{P}(\mathrm{m})\mathrm{P}(\mathrm{b}).

Let’s see if that reading checks out.

Let N be the number of things in general.  Expressed in Peirce’s notation we have the equation [\mathbf{1}] = N.  On the assumption that \mathrm{m} and \mathrm{b} are associated with independent events, we obtain the following sequence of equations.

\begin{array}{lll} [\mathrm{m,} \mathrm{b}] & = & \mathrm{P}(\mathrm{m}\mathrm{b}) N \\[6pt] & = & \mathrm{P}(\mathrm{m}) \mathrm{P}(\mathrm{b}) N \\[6pt] & = & \mathrm{P}(\mathrm{m}) [\mathrm{b}] \\[6pt] & = & [\mathrm{m,}] [\mathrm{b}]. \end{array}

As a result, we have to interpret [\mathrm{m,}] = “the average number of men per things in general” as \mathrm{P}(\mathrm{m}) = “the probability of a thing in general being a man”.  That seems to make sense.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form (1) (2) • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 9 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 11.20

Posted on June 1, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 11.20

We come to the last of Peirce’s statements about the “number of” function, first quoted in Selection 11 and again with the whole set in Comment 11.2.

NOF 4.1

The conception of multiplication we have adopted is that of the application of one relation to another.  […]

Even ordinary numerical multiplication involves the same idea, for 2 \times 3 is a pair of triplets, and 3 \times 2 is a triplet of pairs, where “triplet of” and “pair of” are evidently relatives.

If we have an equation of the form

xy ~=~ z

and there are just as many x’s per y as there are, per things, things of the universe, then we have also the arithmetical equation,

[x][y] ~=~ [z].

(Peirce, CP 3.76)

Peirce here observes what may be called a contingent morphism.  On a condition he gives, the mapping of logical terms to their corresponding numbers preserves the multiplication of relative terms after the fashion of the following formula.

v(xy) = v(x) v(y).

Equivalently:

[xy] = [x][y].

The condition for this to hold is expressed by Peirce in the following manner.

There are just as many x’s per y as there are, per things, things of the universe.

Peirce’s phrasing on this point is admittedly hard to parse but if we stick with his story to the end I think we can see what he’s driving at.

NOF 4.2

For instance, if our universe is perfect men, and there are as many teeth to a Frenchman (perfect understood) as there are to any one of the universe, then

[\mathit{t}][\mathrm{f}] ~=~ [\mathit{t}\mathrm{f}]

holds arithmetically.  (Peirce, CP 3.76).

Now that is something we can sink our teeth into and trace the bigraph representation of the situation.  It will help to recall our first examination of the “tooth of” relation and to adjust the picture we sketched of it on that occasion.

Transcribing Peirce’s example:

\begin{array}{ll} \text{Let} & \mathrm{m} ~=~ \text{man} \\[8pt] \text{and} & \mathit{t} ~=~ \text{tooth of}\,\underline{~~~~}. \\[8pt] \text{Then} & v(\mathit{t}) ~=~ [\mathit{t}] ~=~ \displaystyle\frac{[\mathit{t}\mathrm{m}]}{[\mathrm{m}]}. \end{array}

That is to say, the number of the relative term “tooth of” is equal to the number of teeth of humans divided by the number of humans.  In a universe of perfect human dentition this gives a quotient of 32.

The dyadic relative term \mathit{t} determines a dyadic relation T \subseteq X \times Y, where X contains all the teeth and Y contains all the people under discussion.

To make the case as simple as possible and still cover the point, suppose there are just four people in our universe of discourse and just two of them are French.  The bigraph product below shows the pertinent facts of the case.

Bigraph Product T ◦ F
\text{Figure 52. Bigraph Product}~ T \circ F

In this picture the order of relational composition flows down the page.  For convenience in composing relations, the absolute term \mathrm{f} = \text{Frenchman} is inflected by the comma functor to form the dyadic relative term \mathrm{f,} = \text{Frenchman that is}\,\underline{~~~~}, which in turn determines the idempotent representation of Frenchmen as a subset of mankind, F \subseteq Y \times Y.

By way of a legend for the Figure, we have the following data.

\begin{array}{lllr} \mathrm{m} & = & \mathrm{J} ~+\!\!,~ \mathrm{K} ~+\!\!,~ \mathrm{L} ~+\!\!,~ \mathrm{M} \qquad = & \mathbf{1} \\[6pt] \mathrm{f} & = & \mathrm{K} ~+\!\!,~ \mathrm{M} \\[6pt] \mathrm{f,} & = & \mathrm{K}\!:\!\mathrm{K} ~+\!\!,~ \mathrm{M}\!:\!\mathrm{M} \\[6pt] \mathit{t} & = & (T_{001} ~+\!\!,~ \dots ~+\!\!,~ T_{032}):J & ~+\!\!, \\[6pt] & & (T_{033} ~+\!\!,~ \dots ~+\!\!,~ T_{064}):K & ~+\!\!, \\[6pt] & & (T_{065} ~+\!\!,~ \dots ~+\!\!,~ T_{096}):L & ~+\!\!, \\[6pt] & & (T_{097} ~+\!\!,~ \dots ~+\!\!,~ T_{128}):M \end{array}

We can use this picture to make sense of Peirce’s statement, repeated below.

NOF 4.2

For instance, if our universe is perfect men, and there are as many teeth to a Frenchman (perfect understood) as there are to any one of the universe, then

[\mathit{t}][\mathrm{f}] ~=~ [\mathit{t}\mathrm{f}]

holds arithmetically.  (Peirce, CP 3.76)

In statistical terms, Peirce is saying this:  If the population of Frenchmen is a fair sample of the general population with regard to the factor of dentition, then the morphic equation,

[\mathit{t}\mathrm{f}] ~=~ [\mathit{t}][\mathrm{f}],

whose transpose gives the equation,

[\mathit{t}] ~=~ \displaystyle\frac{[\mathit{t}\mathrm{f}]}{[\mathrm{f}]},

is every bit as true as the defining equation in this circumstance, namely,

[\mathit{t}] ~=~ \displaystyle\frac{[\mathit{t}\mathrm{m}]}{[\mathrm{m}]}.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form (1) (2) • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 9 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 11.19

Posted on May 29, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 11.19

Up to this point in the 1870 Logic of Relatives, Peirce has introduced the “number of” function on logical terms, v : S \to \mathbb{R} such that v : s \mapsto [s], and discussed the extent to which its use as a measure satisfies the relevant measure-theoretic principles, beginning with the following two.

  1. The “number of” map exhibits a certain type of uniformity property, where the value of the measure on a uniformly qualified population is in fact actualized by each member of the population.
  2. The “number of” map satisfies an order morphism principle, where the partial order of logical terms under implication or inclusion is reflected to a moderate degree by the linear order of their measures.

In Selection 4 Peirce takes up the action of the “number of” function on two types of more or less additive operations we normally consider in logic.

NOF 3.1

It is plain that both the regular non-invertible addition and the invertible addition satisfy the absolute conditions.  (CP 3.67).

Peirce uses the sign “+\!\!,” to indicate what he calls the “regular non-invertible addition”, corresponding to the inclusive disjunction of logical terms or the union of their extensions as sets.

Peirce uses the sign “+” to indicate what he calls the “invertible addition”, corresponding to the exclusive disjunction of logical terms or the symmetric difference of their extensions as sets.

NOF 3.2

But the notation has other recommendations.  The conception of taking together involved in these processes is strongly analogous to that of summation, the sum of 2 and 5, for example, being the number of a collection which consists of a collection of two and a collection of five.  (CP 3.67).

A full interpretation of the above remark would require us to pick up the precise technical sense in which Peirce is using the word collection and that would take us back to his logical reconstruction of certain aspects of number theory, all of which I am putting off to another time, but it is still possible to get a rough sense of what he is saying relative to the present frame of discussion.

The “number of” map v : S \to \mathbb{R} evidently induces some sort of morphism with respect to logical sums.  If this were true in the strictest sense, we could remove the question marks from the following dubious equations.

v(x ~+\!\!,~ y) ~ \overset{?}{=} ~ v(x) ~+~ v(y)

Equivalently:

[x ~+\!\!,~ y] ~ \overset{?}{=} ~ [x] ~+~ [y]

Of course, things are not quite that simple when it comes to inclusive disjunctions and set‑theoretic unions, so it is usual to introduce the concept of a sub‑additive measure to describe the principle that does hold here, namely, the following.

v(x ~+\!\!,~ y) ~ \le ~ v(x) ~+~ v(y)

Equivalently:

[x ~+\!\!,~ y] ~ \le ~ [x] ~+~ [y]

That is why Peirce trims his discussion of the point with the following hedge.

NOF 3.3

Any logical equation or inequality in which no operation but addition is involved may be converted into a numerical equation or inequality by substituting the numbers of the several terms for the terms themselves — provided all the terms summed are mutually exclusive.  (CP 3.67).

Finally, a morphism with respect to addition, even a contingently qualified one, must do the right thing on behalf of the additive identity element, as follows.

NOF 3.4

Addition being taken in this sense, nothing is to be denoted by zero, for then

x ~+\!\!,~ 0 ~=~ x

whatever is denoted by x;  and this is the definition of zero.  This interpretation is given by Boole, and is very neat, on account of the resemblance between the ordinary conception of zero and that of nothing, and because we shall thus have

[0] ~=~ 0.

(Peirce, CP 3.67)

With respect to the nullity 0 in S and the number 0 in \mathbb{R}, we have the following equation.

v(0) ~=~ [0] ~=~ 0.

In sum, therefore, it can be said:   A measure only serves which also preserves a due respect for the function of a vacuum in nature.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form (1) (2) • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 11.18

Posted on May 28, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 11.18

An order-preserving map is a special case of a structure-preserving map and the idea of preserving structure, as used in mathematics, means preserving some but not necessarily all the structure of the source domain in the transition to the target domain.  In that vein, we may speak of structure preservation in measure, the suggestion being that a property able to be qualified in manner is potentially able to be quantified in degree, admitting answers to questions like, “How structure-preserving is it?”

Let’s see how this applies to Peirce’s “number of” function v : S \to \mathbb{R}.  Let ``-\!\!\!<\!" denote the implication relation on logical terms, let ``\!\le\!" denote the less than or equal to relation on real numbers, and let x, y be any pair of absolute terms in the syntactic domain S.  Then we observe the following relationships.

\begin{array}{lll} x ~-\!\!\!< y & \Rightarrow & v(x) \le v(y) \end{array}

Equivalently:

\begin{array}{lll} x ~-\!\!\!< y & \Rightarrow & [x] \le [y] \end{array}

Nowhere near the number of logical distinctions on the left sides of the implication arrows are typically preserved as one passes to the linear orderings of real numbers on their right sides but that is not required in order to call the map v : S \to \mathbb{R} order-preserving, or what is known as an order morphism.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 9 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 11.17

Posted on May 27, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 11.17

I think the reader is beginning to get an inkling of the crucial importance of the “number of” function in Peirce’s way of looking at logic.  It is one plank in the bridge from logic to the theories of probability, statistics, and information, in which setting logic forms but a limiting case at one scenic turnout on the expanding vista.  It is one of the ways Peirce forges a link between the eternal, logical, or rational realm and the secular, empirical, or real domain.

With that note of encouragement and exhortation, let us return to the details of the text.

NOF 2

But not only do the significations of  =  and  <  here adopted fulfill all absolute requirements, but they have the supererogatory virtue of being very nearly the same as the common significations.  Equality is, in fact, nothing but the identity of two numbers;  numbers that are equal are those which are predicable of the same collections, just as terms that are identical are those which are predicable of the same classes.  So, to write 5 < 7 is to say that 5 is part of 7, just as to write \mathrm{f} < \mathrm{m} is to say that Frenchmen are part of men.  Indeed, if \mathrm{f} < \mathrm{m}~, then the number of Frenchmen is less than the number of men, and if \mathrm{v} = \mathrm{p}~, then the number of Vice‑Presidents is equal to the number of Presidents of the Senate;  so that the numbers may always be substituted for the terms themselves, in case no signs of operation occur in the equations or inequalities.

(Peirce, CP 3.66)

Peirce observes that the measure \mathit{v} on logical terms preserves the relations of implication or inclusion which impose an ordering on those terms.  Here Peirce uses a single symbol ``\!<\!" to denote the linear ordering on numbers, but also what amounts to the implication ordering on logical terms and the inclusion ordering on classes.  Later he will introduce distinctive symbols for the logical orderings.  The links among terms, sets, and numbers can be pursued in all directions and Peirce has already indicated in an earlier paper how he would construct the integers from sets, that is, from the aggregate denotations of terms.  I will try to get back to that another time.

We have a statement of the following form.

If \mathrm{f} < \mathrm{m} then the number of Frenchmen is less than the number of men.

This goes into symbolic form as follows.

\begin{matrix} \mathrm{f} < \mathrm{m} & \Rightarrow & [\mathrm{f}] < [\mathrm{m}]. \end{matrix}

In this setting the ``\!<\!" on the left is a logical ordering on syntactic terms while the ``\!<\!" on the right is an arithmetic ordering on real numbers.

The question that arises in this case is whether a map between two ordered sets is order-preserving.  In order to formulate the question in more general terms, we may begin with the following set-up.

Let X_1 be a set with the ordering <_1.

Let X_2 be a set with the ordering <_2.

An order relation is typically defined by a set of axioms that determines its properties.  Since we have frequent occasion to view the same set in the light of several different order relations, we often resort to explicit specifications like (X, <_1),\ (X, <_2), and so on to indicate a set with a given ordering.

A map F : (X_1, <_1) \to (X_2, <_2) is order-preserving if and only if a statement of a particular form holds for all x and y in (X_1, <_1), namely, the following.

\begin{matrix} x <_1 y & \Rightarrow & F(x) <_2 F(y). \end{matrix}

The “number of” map v : (S, <_1) \to (\mathbb{R}, <_2) has just this character, as exemplified in the case at hand.

\begin{matrix} \mathrm{f} & < & \mathrm{m} & \Rightarrow & [\mathrm{f}] & < & [\mathrm{m}] \\[6pt] \mathrm{f} & < & \mathrm{m} & \Rightarrow & v(\mathrm{f}) & < & v(\mathrm{m}) \end{matrix}

The ``\!<\!" on the left is read as proper inclusion, in other words, subset of but not equal to, while the ``\!<\!" on the right is read as the usual less than relation.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 12 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 11.16

Posted on May 21, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 11.16

We now have enough material on morphisms to go back and cast a more studied eye on what Peirce is doing with that “number of” function, whose application to a logical term \mathit{t} is indicated by writing the term in square brackets, as [\mathit{t}].  It is convenient to have a prefix notation for the function mapping a term \mathit{t} to a number [\mathit{t}] but Peirce previously reserved the letter ``n" for logical \text{not}, so let’s use v(\mathit{t}) as a variant for [\mathit{t}].

My plan will be nothing less plodding than to work through the statements Peirce made in defining and explaining the “number of” function up to our present place in the paper, namely, the budget of points collected in Comment 11.2.

NOF 1

I propose to assign to all logical terms, numbers;  to an absolute term, the number of individuals it denotes;  to a relative term, the average number of things so related to one individual.  Thus in a universe of perfect men (men), the number of “tooth of” would be 32.  The number of a relative with two correlates would be the average number of things so related to a pair of individuals;  and so on for relatives of higher numbers of correlates.  I propose to denote the number of a logical term by enclosing the term in square brackets, thus [\mathit{t}].

(Peirce, CP 3.65)

The role of the “number of” function may be formalized by assigning it a name and a type, in the present discussion v : S \to \mathbb{R}, where S is a suitable set of signs, a syntactic domain, containing all the logical terms whose numbers we need to evaluate in a given context, and where \mathbb{R} is the set of real numbers.

Transcribing Peirce’s example:

\begin{array}{ll} \text{Let} & \mathrm{m} ~=~ \text{man} \\[8pt] \text{and} & \mathit{t} ~=~ \text{tooth of}\,\underline{~~~~}. \\[8pt] \text{Then} & v(\mathit{t}) ~=~ [\mathit{t}] ~=~ \displaystyle\frac{[\mathit{t}\mathrm{m}]}{[\mathrm{m}]}. \end{array}

To spell it out in words, the number of the relative term ``\text{tooth of}\,\underline{~~~~}" in a universe of perfect human dentition is equal to the number of teeth of humans divided by the number of humans, that is, 32.

The dyadic relative term \mathit{t} determines a dyadic relation T \subseteq X \times Y, where X and Y contain all the teeth and all the people, respectively, under discussion.

A rough indication of the bigraph for T might be drawn as follows, showing just the first few items in the toothy part of X and the peoply part of Y.

Dyadic Relation T
\text{Figure 51. Dyadic Relation}~ T \subseteq X \times Y

Notice that the “number of” function v : S \to \mathbb{R} needs the data represented by the entire bigraph for T in order to compute the value [\mathit{t}].

Finally, one observes this component of T is a function in the direction T : X \to Y, since we are counting only teeth which occupy exactly one mouth of a tooth-bearing creature.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 9 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 11.15

Posted on May 15, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 11.15

I’m going to elaborate a little further on the subject of arrows, morphisms, or structure-preserving mappings, as a modest amount of extra work at this point will repay ample dividends when it comes time to revisit Peirce’s “number of” function on logical terms.

The structure preserved by a structure-preserving map is just the structure we all know and love as a triadic relation.  Very typically, it will be the type of triadic relation that defines the type of binary operation that obeys the rules of a mathematical structure known as a group, that is, a structure satisfying the axioms for closure, associativity, identities, and inverses.

For example, in the case of the logarithm map J we have the following data.

\begin{array}{lcccll} J & : & \mathbb{R} & \gets & \mathbb{R} & \text{(properly restricted)} \\[6pt] K & : & \mathbb{R} & \gets & \mathbb{R} \times \mathbb{R} & \text{where}~ K(r, s) = r + s \\[6pt] L & : & \mathbb{R} & \gets & \mathbb{R} \times \mathbb{R} & \text{where}~ L(u, v) = u \cdot v \end{array}

Real number addition and real number multiplication (suitably restricted) are examples of group operations.  If we write the sign of each operation in brackets as a name for the triadic relation that defines the corresponding group, we have the following set-up.

\begin{matrix} J & : & [+] \gets [\,\cdot\,] \\[6pt] [+] & \subseteq & \mathbb{R} \times \mathbb{R} \times \mathbb{R} \\[6pt] [\,\cdot\,] & \subseteq & \mathbb{R} \times \mathbb{R} \times \mathbb{R} \end{matrix}

It often happens that both group operations are indicated by the same sign, usually one from the set \{ \cdot, *, + \} or simple concatenation, but they remain in general distinct whether considered as operations or as relations, no matter what signs of operation are used.  In such a setting, our chiasmatic theme may run a bit like one of the following two variants.

\textit{The image of the sum is the sum of the images.}

\textit{The image of the product is the sum of the images.}

Figure 50 presents a generic picture for groups G and H.

Group Homomorphism J : G ← H
\text{Figure 50. Group Homomorphism}~ J : G \gets H

In a setting where both groups are written with a plus sign, perhaps even constituting the same group, the defining formula of a morphism, J(L(u, v)) = K(Ju, Jv), takes on the shape J(u + v) = Ju + Jv, which looks analogous to the distributive multiplication of a factor J over a sum (u + v).  That is why morphisms are regarded as generalizations of linear functions and are frequently referred to in those terms.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 11.14

Posted on May 15, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 11.14

Let’s now look at a concrete example of a morphism J, say, one of the mappings of reals into reals commonly known as logarithm functions, where you get to pick your favorite base.

Here we have K(r, s) = r + s and L(u, v) = u \cdot v and the formula J(L(u, v)) = K(Ju, Jv) becomes J(u \cdot v) = J(u) + J(v), where ordinary multiplication and addition are indicated by a dot (\cdot) and a plus sign (+) respectively.

Figure 49 shows how the multiplication, addition, and logarithm operations fit together.

Logarithm Arrow J : {+} ← {⋅}
\text{Figure 49. Logarithm Arrow}~ J : \{ + \} \gets \{ \cdot \}

In short, where the image operation J is the logarithm map, the source operation is the numerical product, and the target operation is the numerical sum, we have the following rule of thumb.

The image of the product is the sum of the images.

\begin{array}{lll} J(u \cdot v) & = & J(u) + J(v) \end{array}

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 10 Comments