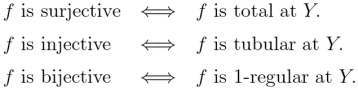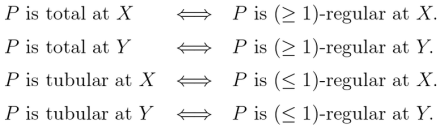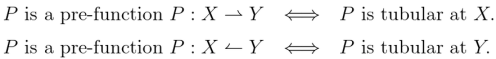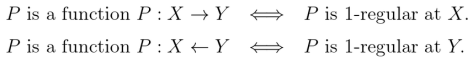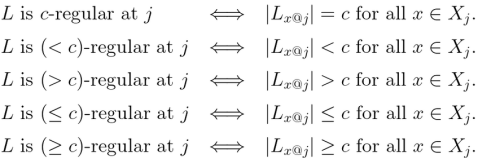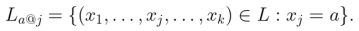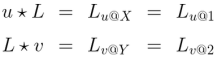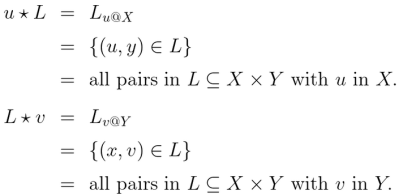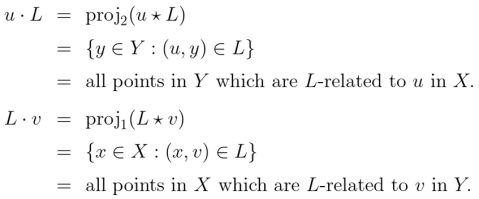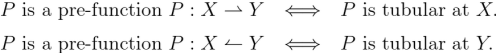Peirce’s 1870 “Logic of Relatives” • Comment 11.13
As we make our way toward the foothills of Peirce’s 1870 Logic of Relatives there are several pieces of equipment we must not leave the plains without, namely, the utilities variously known as arrows, morphisms, homomorphisms, structure-preserving maps, among other names, depending on the altitude of abstraction we happen to be traversing at the moment in question. As a moderate to middling but not too beaten track, let’s examine a few ways of defining morphisms that will serve us in the present discussion.
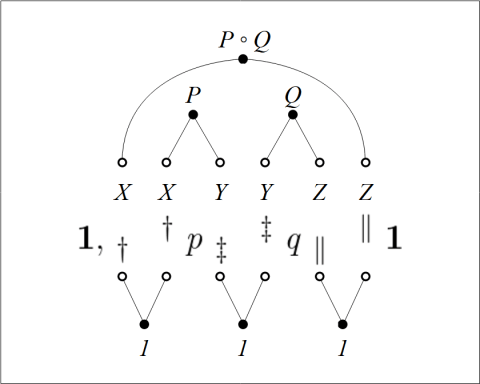
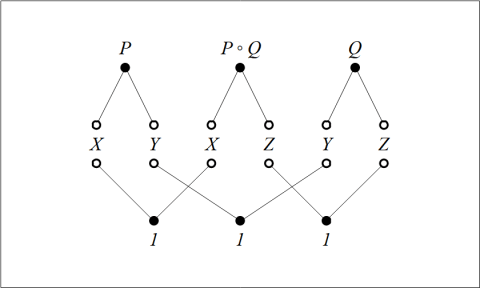
Suppose we are given three functions 
![\begin{array}{lcccl} J & : & X & \gets & Y \\[6pt] K & : & X & \gets & X \times X \\[6pt] L & : & Y & \gets & Y \times Y \end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Blcccl%7D++J+%26+%3A+%26+X+%26+%5Cgets+%26+Y++%5C%5C%5B6pt%5D++K+%26+%3A+%26+X+%26+%5Cgets+%26+X+%5Ctimes+X++%5C%5C%5B6pt%5D++L+%26+%3A+%26+Y+%26+%5Cgets+%26+Y+%5Ctimes+Y++%5Cend%7Barray%7D&bg=ffffff&fg=000000&s=1&c=20201002)
Our sagittarian leitmotif can be rubricized in the following slogan.
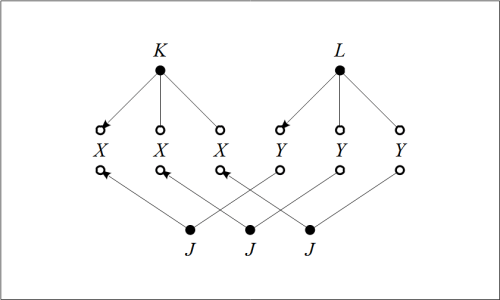
The J-image of the L-product is the K-product of the J-images.
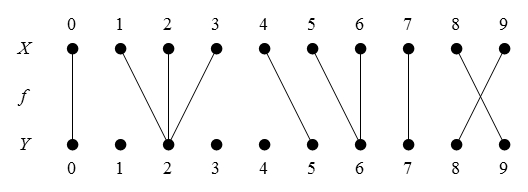
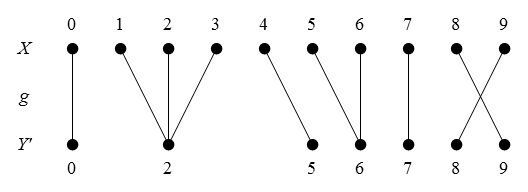
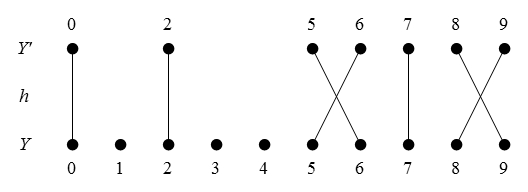
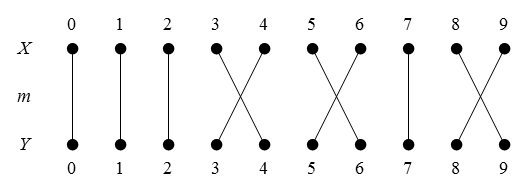
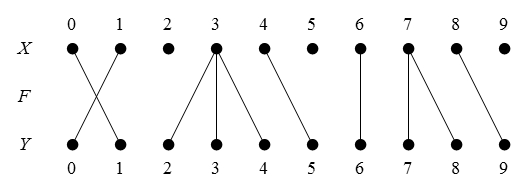
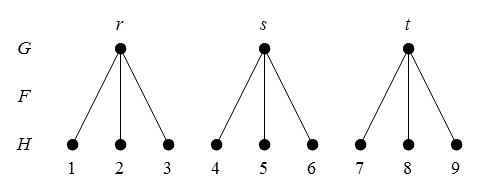
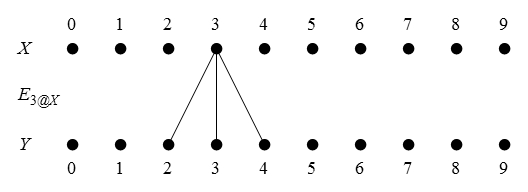
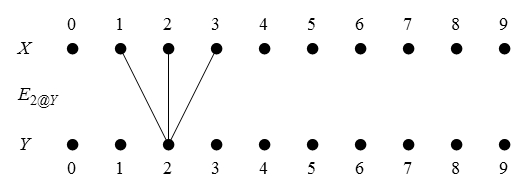
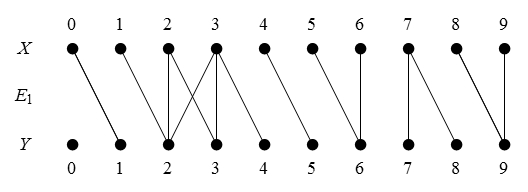
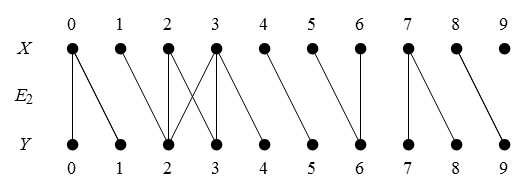
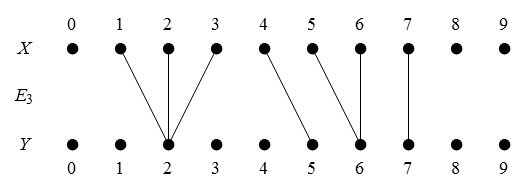
Figure 47 presents us with a picture of the situation in question.
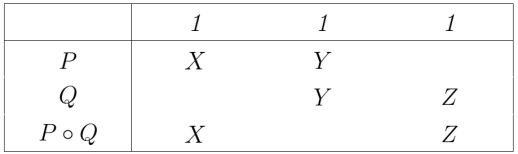
Table 48 gives the constraint matrix version of the same thing.
One way to read the Table is in terms of the informational redundancies it summarizes. For example, one way to read it says that satisfying the constraint in the 
Resources
- Peirce’s 1870 Logic of Relatives • Part 1 • Part 2 • Part 3 • References
- Logic Syllabus • Relational Concepts • Relation Theory • Relative Term
cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)
and 
are assumed to be functional on correlates, a premiss we express as follows.
is also functional on correlates, in symbols, whether 
we have the following equivalence.
For that we have the following formula, where the summation indicated is logical disjunction.
or the fact that 
means there is exactly one ordered pair 
for each 
or the fact that 
means there is exactly one ordered pair 
for each 
for each 
which means 
and so we have the function 
and the corresponding relation 
are both called functional on rèlates if and only if 
We write this in symbols as 
We write this in symbols as 
and 
which qualifies as a function 
may then enjoy a number of further distinctions.
so it can enjoy none of the properties of being surjective, injective, or bijective.
above is 
If we form a new function 
that looks just like 
but is assigned the codomain 
then 
is surjective, and is described as a mapping onto 
is injective.
is bijective.
-regularity conditions where 
-regular, total and tubular, or total prefunctions on specified domains, 
that happens to be total at 
then 
typically indicated as 
and let 
is a function at 
or 
if and only if the cardinality of the local flag 
is equal to 
in 
coded in symbols, if and only if 
for all 
and so on. For ease of reference, a number of such definitions are recorded below.
on one of its domains 
and also 
on the same domain, then it must be 
on that domain, in short, 
at 
and 
and consider the dyadic relation 
bigraphed below.
and 1-regular at 
of a 
-adic relation 
the notation for local flags can be simplified in two ways. First, the local flags 
and 
are often more conveniently notated as 
and 
respectively. Second, the notation may be streamlined even further by making the following definitions.
of 
of 
exemplifies the quality of totality at 
exemplifies the quality of totality at 
exemplifies the quality of tubularity at 
exemplifies the quality of tubularity at 
is a pre-function 
and 
is a pre-function 
and writing 
where 
and where the bigraph picture of 
is shown in Figure 30.
to 
we see that the incidence degrees of the 
in that order.
in that order.
in the following way.![v(t) ~:=~ [t] ~=~ \text{the number of the term}~ t.](https://s0.wp.com/latex.php?latex=v%28t%29+%7E%3A%3D%7E+%5Bt%5D+%7E%3D%7E+%5Ctext%7Bthe+number+of+the+term%7D%7E+t.&bg=ffffff&fg=000000&s=1&c=20201002)
where 
is the set of real numbers and 
is a suitable syntactic domain, here described as a set of terms. The dyadic relation 
is at first sight a function from 
It is, however, not always possible to assign a number to every term in whatever syntactic domain 
means 
is functional at 
means 
means 
means 
written 
amounting to a functional alias of the dyadic relation 
Inquiry Into Inquiry 