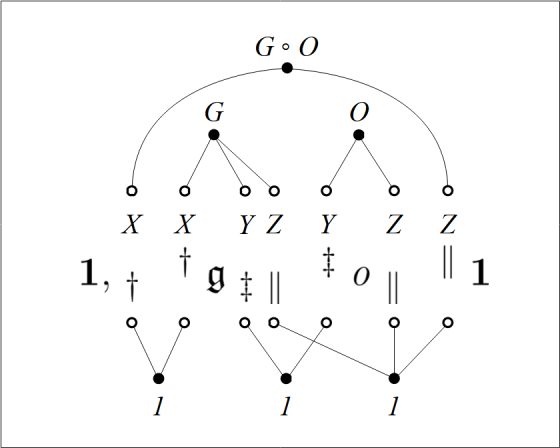
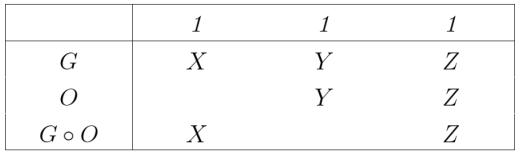
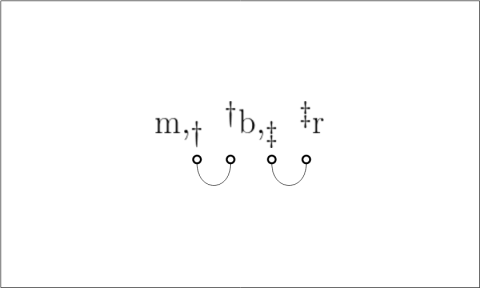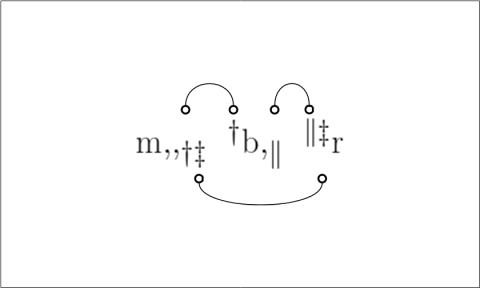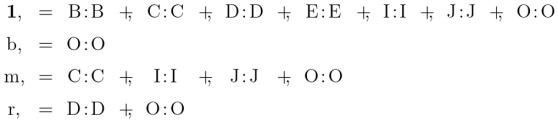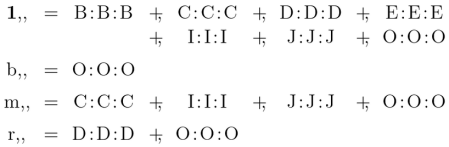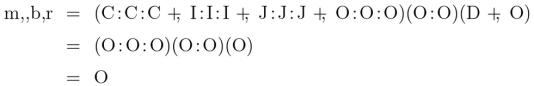Peirce’s 1870 “Logic of Relatives” • Comment 11.3

Posted on April 30, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 11.3

Before I can discuss Peirce’s “number of” function in greater detail I will need to deal with an expositional difficulty I have been carefully dancing around all this time, but one which will no longer abide its assigned place under the rug.

Functions have long been understood, from well before Peirce’s time to ours, as special cases of dyadic relations, so the “number of” function is already to be numbered among the class of dyadic relatives we’ve been dealing with all this time.  But Peirce’s manner of representing a dyadic relative term mentions the “rèlate” first and the “correlate” second, a convention going over into functional terms as making the functional value first and the functional argument second.  The problem is, almost anyone brought up in our present time frame is accustomed to thinking of a function as a set of ordered pairs where the order in each pair lists the functional argument first and the functional value second.

Syntactic wrinkles of this sort can be ironed out smoothly enough in a framework of flexible interpretive conventions, but not without introducing an order of anachronism into Peirce’s text I want to avoid as much as possible.  This will require me to experiment with various styles of compromise.  Among other things, the interpretation of Peirce’s 1870 “Logic of Relatives” can be facilitated by introducing a few items of background material on relations in general, as regarded from a combinatorial point of view.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 11.2

Posted on April 30, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 11.2

NOF Said …

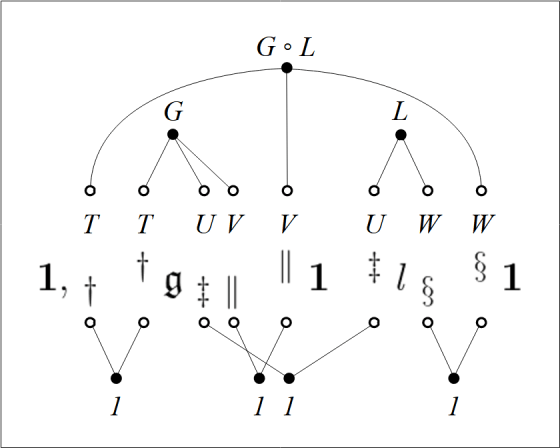
Let’s bring together the various things Peirce has said about the number of function up to this point in the paper.

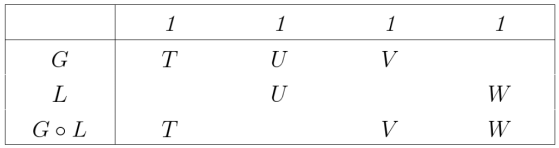
NOF 1

I propose to assign to all logical terms, numbers;  to an absolute term, the number of individuals it denotes;  to a relative term, the average number of things so related to one individual.  Thus in a universe of perfect men (men), the number of “tooth of” would be 32.  The number of a relative with two correlates would be the average number of things so related to a pair of individuals;  and so on for relatives of higher numbers of correlates.  I propose to denote the number of a logical term by enclosing the term in square brackets, thus, [t].

(Peirce, CP 3.65)

NOF 2

But not only do the significations of  =  and 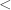 <  here adopted fulfill all absolute requirements, but they have the supererogatory virtue of being very nearly the same as the common significations.  Equality is, in fact, nothing but the identity of two numbers;  numbers that are equal are those which are predicable of the same collections, just as terms that are identical are those which are predicable of the same classes.

So, to write 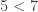5 < 7 is to say that 5 is part of 7, just as to write \mathrm{f} < \mathrm{m} is to say that Frenchmen are part of men.  Indeed, if \mathrm{f} < \mathrm{m}, then the number of Frenchmen is less than the number of men, and if \mathrm{v} = \mathrm{p}, then the number of Vice-Presidents is equal to the number of Presidents of the Senate;  so that the numbers may always be substituted for the terms themselves, in case no signs of operation occur in the equations or inequalities.

(Peirce, CP 3.66)

NOF 3

It is plain that both the regular non-invertible addition and the invertible addition satisfy the absolute conditions.  But the notation has other recommendations.  The conception of taking together involved in these processes is strongly analogous to that of summation, the sum of 2 and 5, for example, being the number of a collection which consists of a collection of two and a collection of five.  Any logical equation or inequality in which no operation but addition is involved may be converted into a numerical equation or inequality by substituting the numbers of the several terms for the terms themselves — provided all the terms summed are mutually exclusive.

Addition being taken in this sense, nothing is to be denoted by zero, for then

x ~+\!\!,~ 0 ~=~ x

whatever is denoted by x;  and this is the definition of zero.  This interpretation is given by Boole, and is very neat, on account of the resemblance between the ordinary conception of zero and that of nothing, and because we shall thus have

[0] ~=~ 0.

(Peirce, CP 3.67)

NOF 4

The conception of multiplication we have adopted is that of the application of one relation to another.  …

Even ordinary numerical multiplication involves the same idea, for 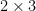2 \times 3 is a pair of triplets, and 3 \times 2 is a triplet of pairs, where “triplet of” and “pair of” are evidently relatives.

If we have an equation of the form

xy ~=~ z,

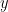and there are just as many x’s per y as there are, per things, things of the universe, then we have also the arithmetical equation,

[x][y] ~=~ [z].

For instance, if our universe is perfect men, and there are as many teeth to a Frenchman (perfect understood) as there are to any one of the universe, then

[\mathit{t}][\mathrm{f}] ~=~ [\mathit{t}\mathrm{f}]

holds arithmetically.

So if men are just as apt to be black as things in general,

[\mathrm{m,}][\mathrm{b}] ~=~ [\mathrm{m,}\mathrm{b}],

where the difference between [\mathrm{m}] and [\mathrm{m,}] must not be overlooked.

It is to be observed that

[\mathit{1}] ~=~ \mathfrak{1}.

Boole was the first to show this connection between logic and probabilities.  He was restricted, however, to absolute terms.  I do not remember having seen any extension of probability to relatives, except the ordinary theory of expectation.

Our logical multiplication, then, satisfies the essential conditions of multiplication, has a unity, has a conception similar to that of admitted multiplications, and contains numerical multiplication as a case under it.

(Peirce, CP 3.76)

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 14 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 11.1

Posted on April 29, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 11.1

Dear Reader,

We have reached a suitable place to pause in our reading of Peirce’s text — actually, it’s more like a place to run as fast as we can along a parallel track — where I can pay off a few of the expository IOUs I’ve been using to pave the way to this point.

The more pressing debts that come to mind are concerned with Peirce’s “number of” function which maps a term t into a number [t] and with my justification for calling a certain style of illustration the hypergraph picture of relational composition.  As it happens, there is a thematic relation between these topics, and so I can make my way forward by addressing them together.

At this point we have two good pictures of how to compute the relational compositions of dyadic relations, namely, the bigraph representation and the matrix representation, each of which has its differential advantages in different types of situations.

But we lack a comparable picture of how to compute the richer variety of relational compositions involving triadic or higher adicity relations.  As a matter of fact, we run into a non-trivial classification problem simply to enumerate the different types of compositions arising in those cases.

Therefore let us inaugurate a systematic study of relational composition, general enough to articulate the “generative potency” of Peirce’s 1870 Logic of Relatives.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Selection 11

Posted on April 29, 2014 by Jon Awbrey

We continue with §3. Application of the Algebraic Signs to Logic.

Peirce’s 1870 “Logic of Relatives” • Selection 11

The Signs for Multiplication (concl.)

The conception of multiplication we have adopted is that of the application of one relation to another.  So, a quaternion being the relation of one vector to another, the multiplication of quaternions is the application of one such relation to a second.

Even ordinary numerical multiplication involves the same idea, for 2 \times 3 is a pair of triplets, and 3 \times 2 is a triplet of pairs, where “triplet of” and “pair of” are evidently relatives.

If we have an equation of the form

xy ~=~ z,

and there are just as many x’s per y as there are, per things, things of the universe, then we have also the arithmetical equation,

[x][y] ~=~ [z].

For instance, if our universe is perfect men, and there are as many teeth to a Frenchman (perfect understood) as there are to any one of the universe, then

[\mathit{t}][\mathrm{f}] ~=~ [\mathit{t}\mathrm{f}]

holds arithmetically.

So if men are just as apt to be black as things in general,

[\mathrm{m,}][\mathrm{b}] ~=~ [\mathrm{m,}\mathrm{b}],

where the difference between [\mathrm{m}] and [\mathrm{m,}] must not be overlooked.

It is to be observed that

[\mathit{1}] ~=~ \mathfrak{1}.

Boole was the first to show this connection between logic and probabilities.  He was restricted, however, to absolute terms.  I do not remember having seen any extension of probability to relatives, except the ordinary theory of expectation.

Our logical multiplication, then, satisfies the essential conditions of multiplication, has a unity, has a conception similar to that of admitted multiplications, and contains numerical multiplication as a case under it.

(Peirce, CP 3.76)

References

  • Peirce, C.S. (1870), “Description of a Notation for the Logic of Relatives, Resulting from an Amplification of the Conceptions of Boole’s Calculus of Logic”, Memoirs of the American Academy of Arts and Sciences 9, 317–378, 26 January 1870.  Reprinted, Collected Papers 3.45–149, Chronological Edition 2, 359–429.  Online (1) (2) (3).
  • Peirce, C.S., Collected Papers of Charles Sanders Peirce, vols. 1–6, Charles Hartshorne and Paul Weiss (eds.), vols. 7–8, Arthur W. Burks (ed.), Harvard University Press, Cambridge, MA, 1931–1935, 1958.
  • Peirce, C.S., Writings of Charles S. Peirce : A Chronological Edition, Peirce Edition Project (eds.), Indiana University Press, Bloomington and Indianapolis, IN, 1981–.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 16 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 10.12

Posted on April 26, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 10.12

Potential ambiguities in Peirce’s two versions of the “rich black man” example can be resolved by providing them with explicit graphical markups, as shown in Figures 28 and 29.

Man that is Black that is Rich

\text{Figure 28. Man that is Black that is Rich}

Man that is a Rich Individual and is a Black Person that is that Rich Individual

\text{Figure 29. Man that is a Rich Individual and is}
\text{a Black Person that is that Rich Individual}

On the other hand, as the forms of relational composition become more complex, the corresponding algebraic products of elementary relatives, for example, \mathrm{(x\!:\!y\!:\!z)(y\!:\!z)(z)}, will not always determine unique results without the addition of more information about the intended linkings of terms.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 10.11

Posted on April 25, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 10.11

Let us return to the point where we left off unpacking the contents of CP 3.73.  Here Peirce remarks that the comma operator can be iterated at will.

In point of fact, since a comma may be added in this way to any relative term, it may be added to one of these very relatives formed by a comma, and thus by the addition of two commas an absolute term becomes a relative of two correlates.

So \mathrm{m,\!,\!b,\!r} interpreted like \mathfrak{g}\mathit{o}\mathrm{h} means a man that is a rich individual and is a black [person] that is that rich individual.  But this has no other meaning than \mathrm{m,\!b,\!r} or a man that is a black [person] that is rich.

Thus we see that, after one comma is added, the addition of another does not change the meaning at all, so that whatever has one comma after it must be regarded as having an infinite number.

(Peirce, CP 3.73)

Again, let’s check whether this makes sense on the stage of our small but dramatic model.  Let’s say Desdemona and Othello are rich and, among the persons of the play, only they.  On this premiss we obtain a sample of absolute terms sufficiently ample to work through Peirce’s example.

Display 1

One application of the comma operator yields the following dyadic relatives.

Display 2

Another application of the comma operator generates the following triadic relatives.

Display 3

Assuming the associativity of multiplication among dyadic relatives, the product \mathrm{m,\!b,\!r} may be computed by a brute force method to yield the following result.

Display 4

This says that a man that is black that is rich is Othello, which is true on the premisses of our present universe of discourse.

Following the standard associative combinations of \mathfrak{g}\mathit{o}\mathrm{h}, the product \mathrm{m,\!,\!b,\!r} is multiplied out along the following lines, where the trinomials of the form \mathrm{(X\!:\!Y\!:\!Z)(Y\!:\!Z)(Z)} are the only ones producing a non‑null result, namely, \mathrm{(X\!:\!Y\!:\!Z)(Y\!:\!Z)(Z) = X}.

Display 5

So we have that \mathrm{m,\!,\!b,\!r} ~=~ \mathrm{m,\!b,\!r}.

In closing, observe how the teridentity relation has turned up again in this context, as the second comma‑ing of the universal term itself.

Display 6

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 10.10

Posted on April 24, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 10.10

The last of Peirce’s three examples involving the composition of triadic relatives with dyadic relatives is shown again in Figure 25.

Lover that is a Servant of a Woman

\text{Figure 25. Lover that is a Servant of a Woman}

The hypergraph picture of the abstract composition is given in Figure 26.

Anything that is a Lover that is a Servant of Anything

\text{Figure 26. Anything that is a Lover that is a Servant of Anything}

This example illustrates the way Peirce analyzes the logical conjunction, we might even say the parallel conjunction, of a pair of dyadic relatives in terms of the comma extension and the same style of composition we saw in the last example, that is, according to a pattern of anaphora invoking the teridentity relation.

Laying out the above analysis of logical conjunction on the spreadsheet model of relational composition, the gist of it is the diagonal extension of a dyadic loving relation L \subseteq X \times Y to a triadic being and loving relation L \subseteq X \times X \times Y, which is then composed with a dyadic serving relation S \subseteq X \times Y so as to determine a dyadic relation L,\!S \subseteq X \times Y.  Table 27 schematizes the associated constraints on tuples.

\text{Table 27. Relational Composition}~ L,S

Relational Composition Table L,S

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 10.9

Posted on April 23, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 10.9

Ergo in numero quo numeramus repetitio unitatum facit pluralitatem;
in rerum vero numero non facit pluralitatem unitatum repetitio,
vel si de eodem dicam “gladius unus mucro unus ensis unus”.

Therefore in the case of that number by which we number,
      the repetition of ones makes a plurality;
but in the number consisting in things
      the repetition of ones does not make a plurality,
as, for example, if I say of one and the same thing,
      “one sword, one brand, one blade”.

Boethius (Anicius Manlius Severinus Boethius, c. 480–524 A.D.),
De Trinitate (The Trinity Is One God Not Three Gods),
The Theological Tractates, H.F. Stewart, E.K. Rand, S.J. Tester (trans.),
New Edition, Loeb Classical Library, Harvard/Heinemann, 1973.

The use of the concepts of identity and teridentity is not to identify a thing-in-itself with itself, much less twice or thrice over — there is no need and thus no utility in that.  I can imagine Peirce asking, on Kantian principles if not entirely on Kantian premisses, “Where is the manifold to be unified?”  The manifold requiring unification does not reside in the object but in the phenomena — in the appearances which might have been appearances of different objects but are bound by the indicated identities to be just so many aspects, facets, parts, roles, or signs of one and the same object.

Notice how the various identity concepts actually functioned in the last example, where they had the opportunity to show their behavior in something like their natural habitat.

Anything that is a Giver of Anything to an Owner of It

\text{Figure 23. Anything that is a Giver of Anything to an Owner of It}

The use of the teridentity concept in the “giver of a horse to an owner of it” is to say the thing appearing with respect to its quality under an absolute term, “a horse”, the thing appearing with respect to its existence as the correlate of a dyadic relative, “a potential possession”, and the thing appearing with respect to its synthesis as the correlate of a triadic relative, “a gift”, are one and the same thing.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 10.8

Posted on April 22, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 10.8

Our progress through the 1870 Logic of Relatives brings us in sight of a critical transition point, one which turns on the teridentity relation.

The markup for Peirce’s “giver of a horse to an owner of it” is shown again in Figure 22.

Giver of a Horse to an Owner of It

\text{Figure 22. Giver of a Horse to an Owner of It}

The hypergraph picture of the abstract composition is given in Figure 23.

Anything that is a Giver of Anything to an Owner of It

\text{Figure 23. Anything that is a Giver of Anything to an Owner of It}

If we analyze this in accord with the spreadsheet model of relational composition then the core of it is a particular way of composing a triadic giving relation G \subseteq X \times Y \times Z with a dyadic owning relation O \subseteq Y \times Z in such a way as to determine a specialized dyadic relation (G \circ O) \subseteq X \times Z.  Table 24 schematizes the associated constraints on tuples.

\text{Table 24. Relational Composition}~ G \circ O

Relational Composition Table G ◦ O

So we see the notorious teridentity relation, which I left equivocally denoted by the same symbol as the identity relation \mathit{1}, is already implicit in Peirce’s discussion at this point.

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 10 Comments

Peirce’s 1870 “Logic of Relatives” • Comment 10.7

Posted on April 18, 2014 by Jon Awbrey

Peirce’s 1870 “Logic of Relatives” • Comment 10.7

Here is what I get when I analyze Peirce’s “giver of a horse to a lover of a woman” example along the same lines as the dyadic compositions.

We may begin with the mark-up shown in Figure 19.

Giver of a Horse to a Lover of a Woman

\text{Figure 19. Giver of a Horse to a Lover of a Woman}

If we analyze this in accord with the spreadsheet model of relational composition then the core of it is a particular way of composing a triadic giving relation G \subseteq T \times U \times V with a dyadic loving relation L \subseteq U \times W so as to obtain a specialized type of triadic relation (G \circ L) \subseteq T \times V \times W.  The applicable constraints on tuples are shown in Table 20.

\text{Table 20. Relational Composition}~ G \circ L

Relational Composition G ◦ L

The hypergraph picture of the abstract composition is given in Figure 21.

Anything that is a Giver of Anything to a Lover of Anything

\text{Figure 21. Anything that is a Giver of Anything to a Lover of Anything}

Resources

cc: Cybernetics • Ontolog Forum • Structural Modeling • Systems Science
cc: FB | Peirce Matters • Laws of Form • Peirce List (1) (2) (3) (4) (5) (6) (7)

Posted in C.S. Peirce, Logic, Logic of Relatives, Logical Graphs, Mathematics, Relation Theory, Visualization | Tagged , , , , , , | 11 Comments