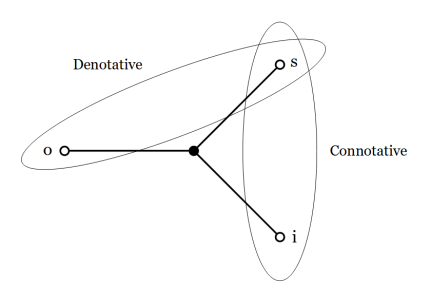
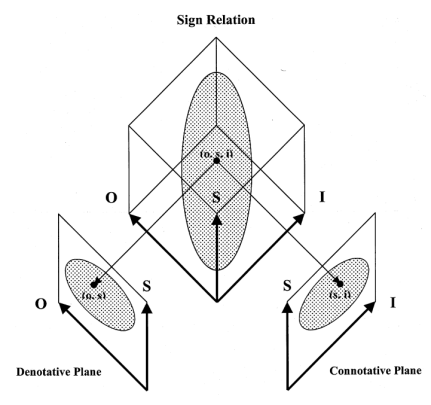
Functional Logic • Inquiry and Analogy
This report discusses C.S. Peirce’s treatment of analogy, placing it in relation to his overall theory of inquiry. We begin by introducing three basic types of reasoning Peirce adopted from classical logic. In Peirce’s analysis both inquiry and analogy are complex programs of logical inference which develop through stages of these three types, though normally in different orders.
Note on notation. The discussion to follow uses logical conjunctions, expressed in the form of concatenated tuples and minimal negation operations, expressed in the form of bracketed tuples
as the principal expression-forming operations of a calculus for boolean-valued functions, that is, for propositions. The expressions of this calculus parse into data structures whose underlying graphs are called cacti by graph theorists. Hence the name cactus language for this dialect of propositional calculus.
Resources
- Logic Syllabus
- Boolean Function
- Boolean-Valued Function
- Logical Conjunction
- Minimal Negation Operator
- Functional Logic • Part 1 • Part 2 • Part 3
- Cactus Language • Part 1 • Part 2 • Part 3 • References • Document History
cc: FB | Peirce Matters • Laws of Form • Mathstodon • Ontolog • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science