Re: Functional Logic • Inquiry and Analogy • 8
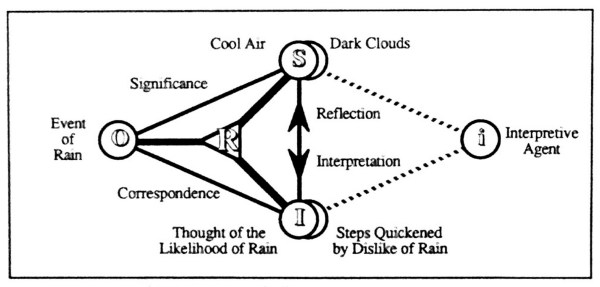
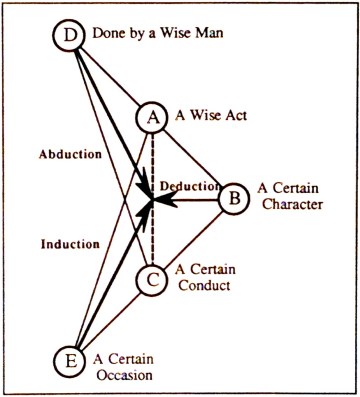
Post 8 used the following Figure to illustrate Dewey’s example of a simple inquiry process.
John Mingers shared the following observations.
- JM:
- Liked the example — a couple of questions/comments.
- In the diagram you have included with the Triadic sign, although with dotted lines, an interpretive agent. Now I thought that Peirce was a bit cagey about this. Wasn’t he clear that the interpretant was not to be identified with an actual interpreter? What is your thinking on this?
- I do agree that there needs to be an interpreter but does it need to be a person? Surely it could be any organism that can interact with relations?
The cool air is something our hero interprets as a sign of rain and his thought of rain is an interpretant sign of the very same object. The relation between the interpretant sign and the interpretive agent is clear enough as far as a beginning level of description goes. But a fully pragmatic, semiotic, and system-theoretic account will demand a more fine-grained analysis of what goes on in the inquiry process.
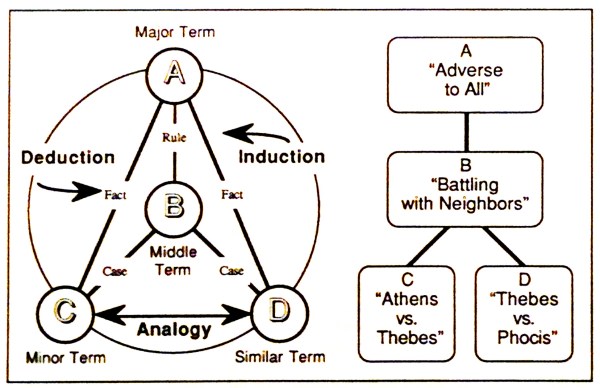
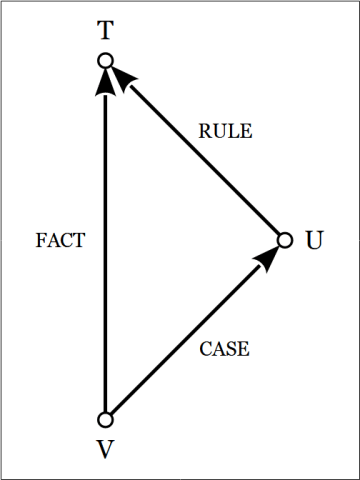
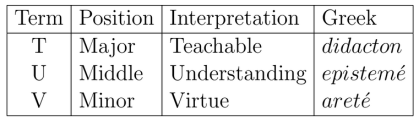
Speaking very roughly, an interpreter is any agent or system — animal, vegetable, or mineral — which actualizes or embodies a triadic sign relation.
Several passages from Peirce will help to flesh out the bare abstractions. I’ll begin collecting them on the linked blog page and discuss them further as we proceed.
Previous Discussions
- 2020
- 2018
- 2001
- 2000
- Semiotics Formalization • Standard Upper Ontology
Related Resources
- Information = Comprehension × Extension • Selection 18
- Inquiry Driven Systems • C’est Moi
- Interpreters and Interpretants
Reference
- Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), 40–52. Archive. Journal. Online (doc) (pdf).
cc: FB | Peirce Matters • Laws of Form • Mathstodon • Ontolog • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science
In the Current situation the Air is cool.
Just Before it rains, the Air is cool.
The Current situation is just Before it rains.
Just Before it rains, a Dark cloud will appear.
In the Current situation, a Dark cloud will appear.
are a random sample of some undefined class 
of whose characters 
are samples,![\begin{matrix} T ~\text{is}~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}; \\[4pt] S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime}, ~\text{are}~ Q\text{'s}; \\[4pt] \text{Hence,}~ T ~\text{is a}~ Q. \end{matrix}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Bmatrix%7D++T+%7E%5Ctext%7Bis%7D%7E+P%5E%7B%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%5Cprime%7D%3B++%5C%5C%5B4pt%5D++S%5E%7B%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%5Cprime%7D%2C+%7E%5Ctext%7Bare%7D%7E+Q%5Ctext%7B%27s%7D%3B++%5C%5C%5B4pt%5D++%5Ctext%7BHence%2C%7D%7E+T+%7E%5Ctext%7Bis+a%7D%7E+Q.++%5Cend%7Bmatrix%7D&bg=ffffff&fg=000000&s=0&c=20201002)
![\begin{array}{l|l} \text{Every}~ X ~\text{is, for example,}~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}, ~\text{etc.}, & S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime}, ~\text{etc., are samples of the}~ X\text{'s}, \\[4pt] T ~\text{is found to be}~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}, ~\text{etc.}; & S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime}, ~\text{etc., are found to be}~ Q\text{'s}; \\[4pt] \text{Hence, hypothetically,}~ T ~\text{is an}~ X. & \text{Hence, inductively, every}~ X ~\text{is a}~ Q. \end{array}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Barray%7D%7Bl%7Cl%7D++%5Ctext%7BEvery%7D%7E+X+%7E%5Ctext%7Bis%2C+for+example%2C%7D%7E+P%5E%7B%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%5Cprime%7D%2C+%7E%5Ctext%7Betc.%7D%2C++%26++S%5E%7B%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%5Cprime%7D%2C+%7E%5Ctext%7Betc.%2C+are+samples+of+the%7D%7E+X%5Ctext%7B%27s%7D%2C++%5C%5C%5B4pt%5D++T+%7E%5Ctext%7Bis+found+to+be%7D%7E+P%5E%7B%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%5Cprime%7D%2C+%7E%5Ctext%7Betc.%7D%3B++%26++S%5E%7B%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%5Cprime%7D%2C+%7E%5Ctext%7Betc.%2C+are+found+to+be%7D%7E+Q%5Ctext%7B%27s%7D%3B++%5C%5C%5B4pt%5D++%5Ctext%7BHence%2C+hypothetically%2C%7D%7E+T+%7E%5Ctext%7Bis+an%7D%7E+X.++%26++%5Ctext%7BHence%2C+inductively%2C+every%7D%7E+X+%7E%5Ctext%7Bis+a%7D%7E+Q.++%5Cend%7Barray%7D&bg=ffffff&fg=000000&s=-1&c=20201002)
are taken at random from such a class that their characters at random are such as 
![\begin{matrix} T ~\text{is}~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}, \\[4pt] S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime} ~\text{are}~ Q; \\[4pt] \therefore T ~\text{is}~ Q. \end{matrix}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Bmatrix%7D++T+%7E%5Ctext%7Bis%7D%7E+P%5E%7B%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%5Cprime%7D%2C++%5C%5C%5B4pt%5D++S%5E%7B%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%5Cprime%7D+%7E%5Ctext%7Bare%7D%7E+Q%3B++%5C%5C%5B4pt%5D++%5Ctherefore+T+%7E%5Ctext%7Bis%7D%7E+Q.++%5Cend%7Bmatrix%7D&bg=ffffff&fg=000000&s=0&c=20201002)
![\begin{matrix} 1. \\[4pt] S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime} ~\text{are taken as being}~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}, \\[4pt] S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime} ~\text{are}~ Q; \\[4pt] \therefore ~(\text{By induction})~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime} ~\text{is}~ Q, \\[4pt] T ~\text{is}~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}; \\[4pt] \therefore ~(\text{Deductively})~ T ~\text{is}~ Q. \end{matrix}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Bmatrix%7D++1.++%5C%5C%5B4pt%5D++S%5E%7B%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%5Cprime%7D+%7E%5Ctext%7Bare+taken+as+being%7D%7E+P%5E%7B%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%5Cprime%7D%2C++%5C%5C%5B4pt%5D++S%5E%7B%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%5Cprime%7D+%7E%5Ctext%7Bare%7D%7E+Q%3B++%5C%5C%5B4pt%5D++%5Ctherefore+%7E%28%5Ctext%7BBy+induction%7D%29%7E+P%5E%7B%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%5Cprime%7D+%7E%5Ctext%7Bis%7D%7E+Q%2C++%5C%5C%5B4pt%5D++T+%7E%5Ctext%7Bis%7D%7E+P%5E%7B%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%5Cprime%7D%3B++%5C%5C%5B4pt%5D++%5Ctherefore+%7E%28%5Ctext%7BDeductively%7D%29%7E+T+%7E%5Ctext%7Bis%7D%7E+Q.++%5Cend%7Bmatrix%7D&bg=ffffff&fg=000000&s=0&c=20201002)
![\begin{matrix} 2. \\[4pt] S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime} ~\text{are, for instance,}~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}, \\[4pt] T ~\text{is}~ P^{\prime}, P^{\prime\prime}, P^{\prime\prime\prime}; \\[4pt] \therefore ~(\text{By hypothesis})~ T ~\text{has the common characters of}~ S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime}, \\[4pt] S^{\prime}, S^{\prime\prime}, S^{\prime\prime\prime} ~\text{are}~ Q; \\[4pt] \therefore ~(\text{Deductively})~ T ~\text{is}~ Q. \end{matrix}](https://s0.wp.com/latex.php?latex=%5Cbegin%7Bmatrix%7D++2.++%5C%5C%5B4pt%5D++S%5E%7B%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%5Cprime%7D+%7E%5Ctext%7Bare%2C+for+instance%2C%7D%7E+P%5E%7B%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%5Cprime%7D%2C++%5C%5C%5B4pt%5D++T+%7E%5Ctext%7Bis%7D%7E+P%5E%7B%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%7D%2C+P%5E%7B%5Cprime%5Cprime%5Cprime%7D%3B++%5C%5C%5B4pt%5D++%5Ctherefore+%7E%28%5Ctext%7BBy+hypothesis%7D%29%7E+T+%7E%5Ctext%7Bhas+the+common+characters+of%7D%7E+S%5E%7B%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%5Cprime%7D%2C++%5C%5C%5B4pt%5D++S%5E%7B%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%7D%2C+S%5E%7B%5Cprime%5Cprime%5Cprime%7D+%7E%5Ctext%7Bare%7D%7E+Q%3B++%5C%5C%5B4pt%5D++%5Ctherefore+%7E%28%5Ctext%7BDeductively%7D%29%7E+T+%7E%5Ctext%7Bis%7D%7E+Q.++%5Cend%7Bmatrix%7D&bg=ffffff&fg=000000&s=0&c=20201002)
is read as 
that is, 
or 
Inquiry Into Inquiry 