Inquiry Into Inquiry

Re: Operator Variables in Logical Graphs • 4

We have encountered the question of how to extend our formal calculus to take account of operator variables.

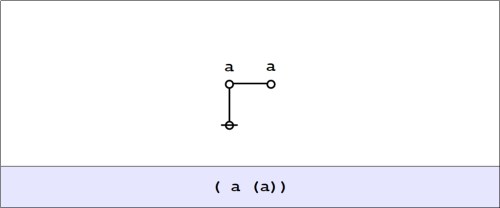
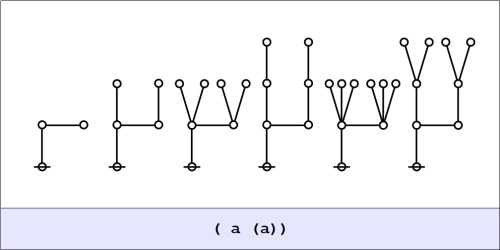
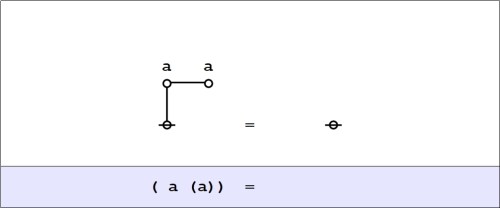
In the days when I scribbled my logical graphs on the backs of computer punchcards, the first thing I tried was drawing big loopy script characters, placing some inside the loops of others.  Lower case alphas, betas, gammas, deltas, and so on worked best.  Graphs like that conveyed the idea that a character-shaped boundary drawn around an enclosed space can be viewed as absent or present depending on whether the formal value of the character in question is unmarked or marked.  The same idea can be conveyed by attaching characters directly to the edges of graphs.

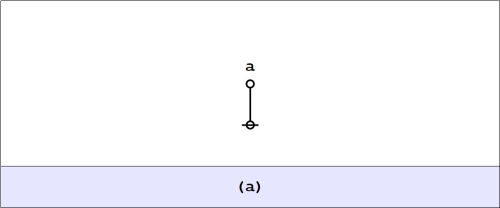
For example, the next Figure shows how we might suggest an algebraic expression of the form where the absence or presence of the operator depends on the value of the algebraic expression the operator being absent whenever is unmarked and present whenever is marked.

It was clear from the outset that this sort of tactic would need a lot of work to become a usable calculus, especially when it came time to feed those punchcards back into the computer.

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Re: Operator Variables in Logical Graphs • 3

Last time we contemplated the penultimately simple algebraic expression as a name for a set of arithmetic expressions, specifically, taking the equal sign in the appropriate sense.

Then we asked the corresponding question about the operator   The above set of arithmetic expressions is what it means to contemplate the absence or presence of the arithmetic constant in the place of the operand in the algebraic expression   But what would it mean to contemplate the absence or presence of the operator in the algebraic expression

Evidently, a variation between the absence and the presence of the operator in the algebraic expression refers to a variation between the algebraic expression and the algebraic expression somewhat as pictured below.

But how shall we signify such variations in a coherent calculus?

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

And if he is told that something is the way it is, then he thinks:  Well, it could probably just as easily be some other way.  So the sense of possibility might be defined outright as the capacity to think how everything could “just as easily” be, and to attach no more importance to what is than to what is not.

— Robert Musil • The Man Without Qualities

To get a clearer view of the relation between primary arithmetic and primary algebra consider the following extremely simple algebraic expression.

Here we see the variable name appearing as an operand name in the expression   In functional terms, is called an argument name but it’s best to avoid the potentially confusing connotations of the word argument here, since it also refers in logical discussions to a more or less specific pattern of reasoning.

In effect, the algebraic variable name indicates the contemplated absence or presence of any arithmetic expression taking its place in the surrounding template, which expression is proxied well enough by its formal value, and of which values we know but two.  Putting it all together, the algebraic expression varies between the following two choices.

The above set of arithmetic expressions is what it means to contemplate the absence or presence of the arithmetic constant in the place of the operand in the algebraic expression   But what would it mean to contemplate the absence or presence of the operator in the algebraic expression

That is the question I’ll take up next.

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Re: Operator Variables in Logical Graphs • 1
Re: Cybernetics List • Lou Kauffman

LK:

I am writing to comment that there are some quite interesting situations that generalize the De Morgan Duality.

One well-known one is this.  Let denote the real numbers with a formal symbol denoting infinity, adjoined so that:

(Of course you cannot do anything with or the system collapses.  One can easily give the constraints.)

Define

Define

Then we have so that the system satisfies De Morgan duality and it is a Boolean algebra when restricted to

Note also that fixes and   This algebraic system occurs of course in electrical calculations and also in the properties of tangles in knot theory, as you can read in the last part of my included paper “Knot Logic”.  I expect there is quite a bit more about this kind of duality in various (categorical) places.

Thanks, Lou, there’s a lot to think about here, so I’ll need to study it a while.  Just off hand, the embedding into reals brings up a vague memory of the very curious way Peirce defines negation in his 1870 “Logic of Relatives”.  I seem to recall it involving a power series, but it’s been a while so I’ll have to look it up again.

Regards,

Jon

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Re: Operator Variables in Logical Graphs • 1
Re: Academia.edu • Stephen Duplantier

SD:

The best way for me to read Peirce is as if he was writing poetry.  So if his algebra is poetry — I imagine him approving of the approach since he taught me abduction in the first place — there is room to wander.  With this, I venture the idea that his “wide field” is a local algebraic geography far from the tended garden.  There, where weeds and wild things grow and hybridize are the non‑dichotomic mathematics.

“Abdeuces Are Wild”, as they say, maybe not today, maybe not tomorrow, but soon …

As far as my own guess, and a lot of my wandering in pursuit of it goes, I’d venture Peirce’s field of vision opens up not so much from dichotomic to trichotomic domains of value as from dyadic to triadic relations, and all that with particular significance into the medium of reflection afforded by triadic sign relations.

Resources

• Logic Syllabus
• Semeiotic
• Sign Relations
• Triadic Relations

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Operand Variables

In George Spencer Brown’s Laws of Form the relation between the primary arithmetic and the primary algebra is founded on the idea that a variable name appearing as an operand in an algebraic expression indicates the contemplated absence or presence of any expression in the arithmetic, with the understanding that each appearance of the same variable name indicates the same state of contemplation with respect to the same expression of the arithmetic.

For example, consider the following expression:

We may regard this algebraic expression as a general expression for an infinite set of arithmetic expressions, starting like so:

Now consider what that says about the following algebraic law:

It permits us to understand the algebraic law as saying, in effect, that every one of the arithmetic expressions of the contemplated pattern evaluates to the very same canonical expression as the upshot of that evaluation.  That is, as far as I know, just about as close as we come to a conceptually and ontologically minimal way of understanding the relation between an algebra and its corresponding arithmetic.

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

In lieu of a field study requirement for my bachelor’s degree I spent two years in various state and university libraries reading everything I could find by and about Peirce, poring most memorably through reels of microfilmed Peirce manuscripts Michigan State had at the time, all in trying to track down some hint of a clue to a puzzling passage in Peirce’s “Simplest Mathematics”, most acutely coming to a head with that bizarre line of type at CP 4.306, which the editors of Peirce’s Collected Papers, no doubt compromised by the typographer’s reluctance to cut new symbols, transmogrified into a script more cryptic than even the manuscript’s original hieroglyphic.

I found one key to the mystery in Peirce’s use of operator variables, which he and his students Christine Ladd‑Franklin and O.H. Mitchell explored in depth.  I will shortly discuss that theme as it affects logical graphs but it may be useful to give a shorter and sweeter explanation of how the basic idea typically arises in common logical practice.

Consider De Morgan’s rules:

The common form exhibited by the two rules could be captured in a single formula by taking and as variable names ranging over a family of logical operators, then asking what substitutions for and would satisfy the following equation.

We already know two solutions to this operator equation, namely, and   Wouldn’t it be just like Peirce to ask if there are others?

Having broached the subject of logical operator variables, I will leave it for now in the same way Peirce himself did:

I shall not further enlarge upon this matter at this point, although the conception mentioned opens a wide field;  because it cannot be set in its proper light without overstepping the limits of dichotomic mathematics.  (Collected Papers, CP 4.306).

Further exploration of operator variables and operator invariants treads on grounds traditionally known as second intentional logic and “opens a wide field”, as Peirce says.  For now, however, I will tend to that corner of the field where our garden variety logical graphs grow, observing the ways in which operative variations and operative themes naturally develop on those grounds.

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science