Inquiry Into Inquiry

Interpretive Duality in Logical Graphs • 3

Posted on April 24, 2024 by Jon Awbrey

Re: Interpretive Duality in Logical Graphs • (1) • (2)

For a sense of how the choice of interpretation bears on cases beyond the bare minimum complexity let us start with the familiar example of Peirce’s law, commonly expressed in the following form.

$((p \Rightarrow q) \Rightarrow p) \Rightarrow p$

The following two formal equations show how Peirce’s law may be expressed in terms of logical graphs, operating under the entitative and existential interpretations, respectively.

$\text{Peirce's Law} \stackrel{_\bullet}{} \text{Dual Graphs}$

Resources

Peirce’s Law • (1) • (2) • (3) • (4) • (5) • (6) • (7)

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Interpretive Duality, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Visualization | Tagged Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Interpretive Duality, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Visualization | 5 Comments

Interpretive Duality in Logical Graphs • 2

Posted on April 23, 2024 by Jon Awbrey

Re: Interpretive Duality in Logical Graphs • 1

A logical concept represented by a boolean variable has its extension, the cases it covers in a designated universe of discourse, and its comprehension (or intension), the properties it implies in a designated hierarchy of predicates.

The formulas and graphs tabulated in the previous post are well‑adapted to articulate the syntactic and intensional aspects of propositional logic. But their very tailoring to those tasks tends to slight the extensional and therefore empirical applications of logic. Venn diagrams, despite their unwieldiness as the number of logical dimensions increases, are indispensable in providing the visual intuition with a solid grounding in the extensions of logical concepts. All that makes it worthwhile to reset our table of boolean functions on two variables to include the corresponding venn diagrams.

$\text{Venn Diagrams and Logical Graphs on Two Variables}$

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Interpretive Duality in Logical Graphs • 1

Posted on April 22, 2024 by Jon Awbrey

The duality between Entitative and Existential interpretations of logical graphs is a good example of a mathematical symmetry, in this case a symmetry of order two. Symmetries of this and higher orders give us conceptual handles on excess complexity in the manifold of sensuous impressions, making it well worth the effort to seek them out and grasp them where we find them.

Both Peirce and Spencer Brown understood the significance of the mathematical unity underlying the dual interpretation of logical graphs. Peirce began with the Entitative option and later switched to the Existential choice while Spencer Brown exercised the Entitative option in his Laws of Form.

In that vein, here’s a Rosetta Stone to give us a grounding in the relationship between boolean functions and our two readings of logical graphs.

$\text{Boolean Functions on Two Variables}$

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Operator Variables in Logical Graphs • 12

Posted on April 21, 2024 by Jon Awbrey

Re: Operator Variables in Logical Graphs • 11

The rules given in the previous post for evaluating cactus graphs were given in purely formal terms, that is, by referring to the mathematical forms of cacti without mentioning their potential for logical meaning. As it turns out, two ways of mapping cactus graphs to logical meanings are commonly found in practice. These two mappings of mathematical structure to logical meaning are formally dual to each other and known as the Entitative and Existential interpretations respectively. The following Table compares the entitative and existential interpretations of the primary cactus structures, from which the rest of their semantics can be derived.

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | Tagged Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | 4 Comments

Operator Variables in Logical Graphs • 11

Posted on April 20, 2024 by Jon Awbrey

Re: Futures Of Logical Graphs • Themes and Variations

This post and the next wrap up the Themes and Variations section of my speculation on Futures of Logical Graphs. I made an effort to “show my work”, reviewing the steps I took to arrive at the present perspective on logical graphs, whistling past the least productive of the blind alleys, cul‑de‑sacs, detours, and forking paths I explored along the way. It can be useful to tell the story that way, partly because others may find things I missed down those roads, but it does call for a recap of the main ideas I would like readers to take away.

Partly through my reflection on Peirce’s use of operator variables I was led to what I called a “reflective extension of logical graphs”, amounting to a graphical formal language called the “cactus language” or “cactus syntax” after its principal graph-theoretic data structure.

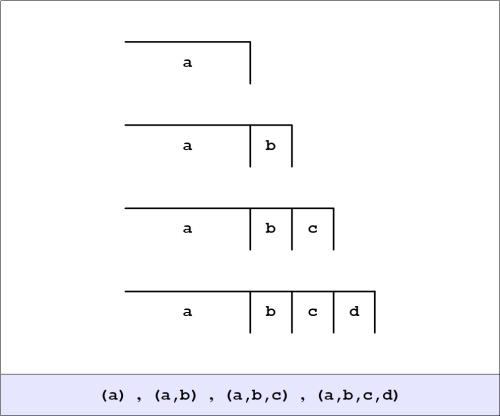
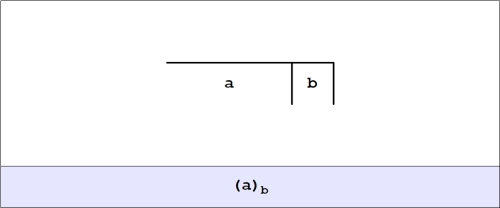
The abstract syntax of cactus graphs can be interpreted for logical use in a couple of ways, both of which arise from generalizing the negation operator ${}^{\backprime\backprime} \texttt{(} ~ \texttt{)} {}^{\prime\prime}$ in a particular direction, treating ${}^{\backprime\backprime} \texttt{(} ~ \texttt{)} {}^{\prime\prime}$ as the controlled, moderated, or reflective negation operator of order 1 and adding another operator for each integer greater than 1. 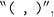The resulting family of operators is symbolized by bracketed argument lists of the forms ${}^{\backprime\backprime} \texttt{(} ~ \texttt{)} {}^{\prime\prime},$ ${}^{\backprime\backprime} \texttt{(} ~ \texttt{,} ~ \texttt{)} {}^{\prime\prime},$ ${}^{\backprime\backprime} \texttt{(} ~ \texttt{,} ~ \texttt{,} ~ \texttt{)} {}^{\prime\prime},$ and so on, where the number of places is the order of the reflective negation operator in question.

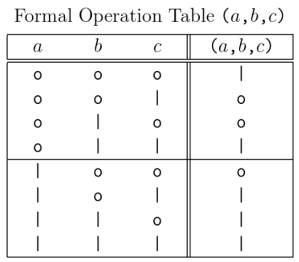
Two rules suffice for evaluating cactus graphs.

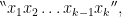The rule for evaluating a $k$ -node operator, corresponding to an expression of the form ${}^{\backprime\backprime} x_1 x_2 \ldots x_{k-1} x_k {}^{\prime\prime},$ is as follows.

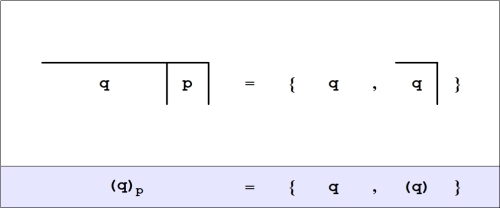
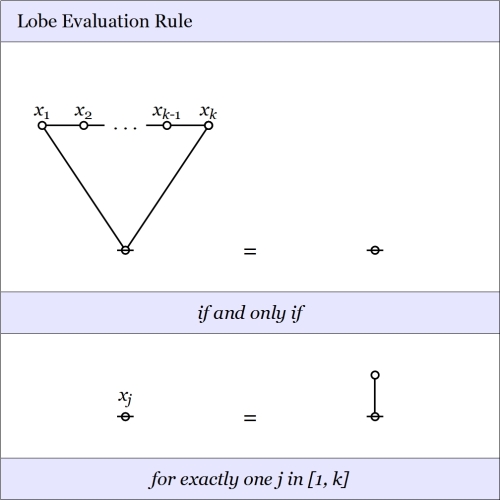
The rule for evaluating a $k$ -lobe operator, corresponding to an expression of the form ${}^{\backprime\backprime} \texttt{(} x_1 \texttt{,} x_2 \texttt{,} \ldots \texttt{,} x_{k-1} \texttt{,} x_k \texttt{)} {}^{\prime\prime},$ is as follows.

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | Tagged Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | 5 Comments

Operator Variables in Logical Graphs • 10

Posted on April 18, 2024 by Jon Awbrey

Re: Operator Variables in Logical Graphs • 9

Let’s examine the Formal Operation Table for the third in our series of reflective forms to see if we can elicit the general pattern.

Alternatively, if we think in terms of the corresponding cactus graphs, writing ${}^{\backprime\backprime} \texttt{o} {}^{\prime\prime}$ for an unmarked node and ${}^{\backprime\backprime} \texttt{|} {}^{\prime\prime}$ for a terminal edge, we get the following Table.

Evidently, the rule is that ${}^{\backprime\backprime} \texttt{(} a \texttt{,} b \texttt{,} c \texttt{)} {}^{\prime\prime}$ denotes the value denoted by ${}^{\backprime\backprime} \texttt{o} {}^{\prime\prime}$ if and only if exactly one of the variables $a, b, c$ has the value denoted by ${}^{\backprime\backprime} \texttt{|} {}^{\prime\prime},$ otherwise ${}^{\backprime\backprime} \texttt{(} a \texttt{,} b \texttt{,} c \texttt{)} {}^{\prime\prime}$ denotes the value denoted by ${}^{\backprime\backprime} \texttt{|} {}^{\prime\prime}.$ Examining the whole series of reflective forms shows this to be the general rule.

In the Entitative Interpretation $(\mathrm{En}),$ where $\texttt{o}$ = false and $\texttt{|}$ = true,
${}^{\backprime\backprime} \texttt{(} x_1 \texttt{,} \ldots \texttt{,} x_k \texttt{)} {}^{\prime\prime}$ translates as “not just one of the $x_j$ is true”.

In the Existential Interpretation $(\mathrm{Ex}),$ where $\texttt{o}$ = true and $\texttt{|}$ = false,
${}^{\backprime\backprime} \texttt{(} x_1 \texttt{,} \ldots \texttt{,} x_k \texttt{)} {}^{\prime\prime}$ translates as “just one of the $x_j$ is not true”.

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | Tagged Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | 4 Comments

Operator Variables in Logical Graphs • 9

Posted on April 17, 2024 by Jon Awbrey

The following Table will suffice to show how the “streamer‑cross” forms C.S. Peirce used in his essay on “Qualitative Logic” and Spencer Brown used in his Laws of Form, as they are extended through successive steps of controlled reflection, translate into syntactic strings and rooted cactus graphs.

$\text{Syntactic Correspondences}$

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | Tagged Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | 5 Comments

Operator Variables in Logical Graphs • 8

Posted on April 16, 2024 by Jon Awbrey

Re: Operator Variables in Logical Graphs • 7

A trick of discovery I learned by observing Peirce’s working methods, more than anything he wrote outright, might be put in the following words.

Take what is constant, Treat it as variable, See if anything remains the same.

The step of controlled reflection we took with the previous post can be repeated at will, as suggested by the following series of forms.

Written inline, we have the series ${}^{\backprime\backprime} \texttt{(} a \texttt{)} {}^{\prime\prime},$ ${}^{\backprime\backprime} \texttt{(} a \texttt{,} b \texttt{)} {}^{\prime\prime},$ ${}^{\backprime\backprime} \texttt{(} a \texttt{,} b \texttt{,} c \texttt{)} {}^{\prime\prime},$ ${}^{\backprime\backprime} \texttt{(} a \texttt{,} b \texttt{,} c \texttt{,} d \texttt{)} {}^{\prime\prime},$ and so on, whose general form is ${}^{\backprime\backprime} \texttt{(} x_1 \texttt{,} x_2 \texttt{,} \ldots \texttt{,} x_k \texttt{)} {}^{\prime\prime}.$ With this move we have passed beyond the graph-theoretical form of rooted trees to what graph theorists know as rooted cacti.

I will discuss this cactus language and its logical interpretations next.

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | Tagged Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | 4 Comments

Operator Variables in Logical Graphs • 7

Posted on April 15, 2024 by Jon Awbrey

Re: Operator Variables in Logical Graphs • 6

A funny thing just happened. Let’s see if we can tell where. We started with the algebraic expression ${}^{\backprime\backprime} \texttt{(} a \texttt{)} {}^{\prime\prime},$ where the operand ${}^{\backprime\backprime} a {}^{\prime\prime}$ suggests the contemplated absence or presence of an arbitrary arithmetic expression. Next we contemplated the absence or presence of the operator ${}^{\backprime\backprime} \texttt{(} ~ \texttt{)} {}^{\prime\prime}$ in ${}^{\backprime\backprime} \texttt{(} a \texttt{)} {}^{\prime\prime}$ to be determined by the value of a newly introduced variable, say ${}^{\backprime\backprime} b {}^{\prime\prime},$ which is placed in a new slot of a newly extended operator form, as suggested by the following Figure.

What happened here is this. Our contemplation of a constant operator as being potentially variable gave rise to the contemplation of a newly introduced but otherwise quite ordinary operand variable, albeit in a newly-fashioned formula. In its interpretation for logic the newly formed operation may be viewed as an extension of ordinary negation, one in which the negation of the first variable is controlled by the value of the second variable.

We may regard this development as marking a form of controlled reflection, or a form of reflective control. From here on out we’ll use the inline syntax ${}^{\backprime\backprime} \texttt{(} a \texttt{,} b \texttt{)} {}^{\prime\prime}$ to indicate the corresponding operation on two variables, whose formal operation table is given below.

The Entitative Interpretation $(\mathrm{En}),$ for which $\texttt{Space} = \texttt{False}$ and $\texttt{Cross} = \texttt{True},$
calls this operation logical equality.
The Existential Interpretation $(\mathrm{Ex}),$ for which $\texttt{Space} = \texttt{True}$ and $\texttt{Cross} = \texttt{False},$
calls this operation logical difference.

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | Tagged Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | 5 Comments

Operator Variables in Logical Graphs • 6

Posted on April 14, 2024 by Jon Awbrey

Another tactic I tried by way of porting operator variables into Peirce’s logical graphs and Spencer Brown’s logical forms was to hollow out a leg of the latter’s crosses, gnomons, or markers, whatever you wish to call them, as shown below.

$Transitional Form (q)_p = {q,(q)}$

The initial idea I had in mind was the same as before, that the operator over $q$ would be counted as absent when $p$ evaluates to a space and present when $p$ evaluates to a cross.

However, much in the same way operators with a shade of negativity tend to be more generative than the purely positive brand, it turned out more useful to reverse the initial polarity of operation, letting the operator over $q$ be counted as absent when $p$ evaluates to a cross and present when $p$ evaluates to a space.

So that is the convention I’ll adopt from this point on.

cc: FB | Logical Graphs • Laws of Form • Ma^thstodon • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | Tagged Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | 5 Comments

	Survey of Differenti… on Differential Logic • 4
	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…
	Differential Logic •… on Logic Syllabus
	Survey of Differenti… on Differential Logic • 3
	Survey of Differenti… on Differential Logic • 2
	Survey of Differenti… on Differential Logic • 1
	Survey of Differenti… on Differential Logic • Over…
	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…

Inquiry Into Inquiry

Interpretive Duality in Logical Graphs • 3

Resources

Interpretive Duality in Logical Graphs • 2

Interpretive Duality in Logical Graphs • 1

Operator Variables in Logical Graphs • 12

Operator Variables in Logical Graphs • 11

Operator Variables in Logical Graphs • 10

Operator Variables in Logical Graphs • 9

Operator Variables in Logical Graphs • 8

Operator Variables in Logical Graphs • 7

Operator Variables in Logical Graphs • 6

Elsewhere

Blogroll

Follow Blog via Email

Recent Posts

Recent Comments

Archives

Blog Stats

Categories

Logic, Mathematics, Philosophy

Inquiry Driven Systems

Cybernetics

Differential Logic

Logical Graphs

Minimal Negation Operators

Peirce Matters

Relation Theory

Riffs & Rotes

Semeiotics

Theme One

Current Events

Fawkes News

Meta

Resources

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Share this:

Elsewhere

Blogroll

Follow Blog via Email

Recent Posts

Recent Comments

Archives

Blog Stats

Categories

Logic, Mathematics, Philosophy

Current Events

Meta