Inquiry Into Inquiry

Functional Logic • Inquiry and Analogy • 4

Posted on June 24, 2023 by Jon Awbrey

Inquiry and Analogy • Aristotle’s “Apagogy” • Abductive Reasoning

Peirce’s notion of abductive reasoning is derived from Aristotle’s treatment of it in the Prior Analytics. Aristotle’s discussion begins with an example which may seem incidental but the question and its analysis are echoes of the investigation pursued in one of Plato’s Dialogue, the Meno. It concerns nothing less than the possibility of knowledge and the relationship between knowledge and virtue, or between their objects, the true and the good. It is not just because it forms a recurring question in philosophy, but because it preserves a close correspondence between its form and its content, that we shall find this example increasingly relevant to our study.

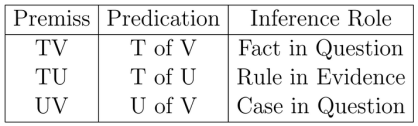
We have Reduction (απαγωγη, abduction): (1) when it is obvious that the first term applies to the middle, but that the middle applies to the last term is not obvious, yet nevertheless is more probable or not less probable than the conclusion; or (2) if there are not many intermediate terms between the last and the middle; for in all such cases the effect is to bring us nearer to knowledge.

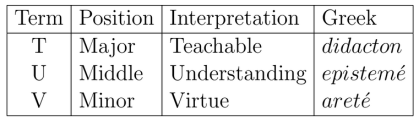
(1) E.g., let A stand for “that which can be taught”, B for “knowledge”, and C for “morality”. Then that knowledge can be taught is evident; but whether virtue is knowledge is not clear. Then if BC is not less probable or is more probable than AC, we have reduction; for we are nearer to knowledge for having introduced an additional term, whereas before we had no knowledge that AC is true.

(2) Or again we have reduction if there are not many intermediate terms between B and C; for in this case too we are brought nearer to knowledge. E.g., suppose that D is “to square”, E “rectilinear figure”, and F “circle”. Assuming that between E and F there is only one intermediate term — that the circle becomes equal to a rectilinear figure by means of lunules — we should approximate to knowledge.

Aristotle, “Prior Analytics” 2.25, Hugh Tredennick (trans.)

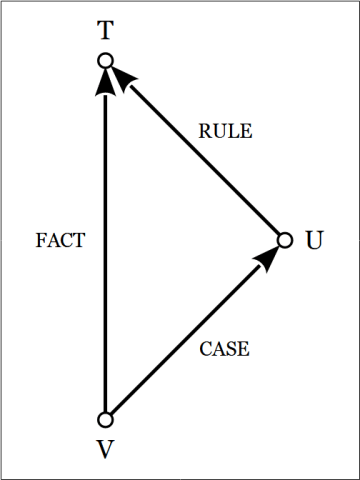
A few notes on the reading may be helpful. The Greek text seems to imply a geometric diagram, in which directed line segments AB, BC, AC indicate logical relations between pairs of terms taken from A, B, C. We have two options for reading the line labels, either as implications or as subsumptions, as in the following two paradigms for interpretation.

In the latter case, $P \geqslant Q$ is read as $``P ~\text{subsumes}~ Q",$ that is, $``P ~\text{applies to all}~ Q",$ or $``P ~\text{is predicated of all}~ Q".$

The method of abductive reasoning bears a close relation to the sense of reduction in which we speak of one question reducing to another. The question being asked is “Can virtue be taught?” The type of answer which develops is as follows.

If virtue is a form of understanding, and if we are willing to grant that understanding can be taught, then virtue can be taught. In this way of approaching the problem, by detour and indirection, the form of abductive reasoning is used to shift the attack from the original question, whether virtue can be taught, to the hopefully easier question, whether virtue is a form of understanding.

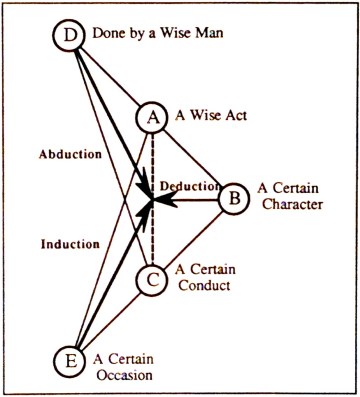
The logical structure of the process of hypothesis formation in the first example follows the pattern of “abduction to a case”, whose abstract form is diagrammed and schematized in Figure 5.

$\text{Figure 5. Teachability, Understanding, Virtue}$

The sense of the Figure is explained by the following assignments.

Abduction from a Fact to a Case proceeds according to the following schema.

$\begin{array}{l} ~ \text{Fact:}~ V \Rightarrow T? \\ ~ \text{Rule:}~ U \Rightarrow T. \\ \overline{~~~~~~~~~~~~~~~~~~~~~~} \\ ~ \text{Case:}~ V \Rightarrow U? \end{array}$

Resources

Logic Syllabus
Boolean Function
Boolean-Valued Function
Logical Conjunction
Minimal Negation Operator
Functional Logic • Part 1 • Part 2 • Part 3
Cactus Language • Part 1 • Part 2 • Part 3 • References • Document History

cc: FB | Peirce Matters • Laws of Form • Mathstodon • Ontolog • Academia.edu (1) (2)
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Posted in Abduction, Analogy, Argument, Aristotle, C.S. Peirce, Constraint, Deduction, Determination, Diagrammatic Reasoning, Diagrams, Differential Logic, Functional Logic, Hypothesis, Indication, Induction, Inference, Information, Inquiry, Logic, Logic of Science, Mathematics, Pragmatic Semiotic Information, Probable Reasoning, Propositional Calculus, Propositions, Reasoning, Retroduction, Semiotics, Sign Relations, Syllogism, Triadic Relations, Visualization | Tagged Abduction, Analogy, Argument, Aristotle, C.S. Peirce, Constraint, Deduction, Determination, Diagrammatic Reasoning, Diagrams, Differential Logic, Functional Logic, Hypothesis, Indication, Induction, Inference, Information, Inquiry, Logic, Logic of Science, Mathematics, Pragmatic Semiotic Information, Probable Reasoning, Propositional Calculus, Propositions, Reasoning, Retroduction, Semiotics, Sign Relations, Syllogism, Triadic Relations, Visualization | 4 Comments

Functional Logic • Inquiry and Analogy • 3

Posted on June 23, 2023 by Jon Awbrey

Inquiry and Analogy • Comparison of the Analyses

The next two Figures will be of use when we turn to comparing the three types of inference as they appear in the respective analyses of Aristotle and Peirce.

Types of Reasoning in Transition

$\text{Figure 3. Types of Reasoning in Transition}$

Types of Reasoning in Peirce

$\text{Figure 4. Types of Reasoning in Peirce}$

Resources

Logic Syllabus
Boolean Function
Boolean-Valued Function
Logical Conjunction
Minimal Negation Operator
Functional Logic • Part 1 • Part 2 • Part 3
Cactus Language • Part 1 • Part 2 • Part 3 • References • Document History

cc: FB | Peirce Matters • Laws of Form • Mathstodon • Ontolog • Academia.edu (1) (2)
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Functional Logic • Inquiry and Analogy • 2

Posted on June 22, 2023 by Jon Awbrey

Inquiry and Analogy • Three Types of Reasoning

Types of Reasoning in C.S. Peirce

Peirce gives one of his earliest treatments of the three types of reasoning in his Harvard Lectures of 1865 “On the Logic of Science”. There he shows how the same proposition may be reached from three directions, as the result of an inference in each of the three modes.

We have then three different kinds of inference.

Deduction or inference à priori,
Induction or inference à particularis,
Hypothesis or inference à posteriori.

(Peirce, CE 1, 267).

If I reason that certain conduct is wise because it has a character which belongs only to wise things, I reason à priori.
If I think it is wise because it once turned out to be wise, that is, if I infer that it is wise on this occasion because it was wise on that occasion, I reason inductively [à particularis].
But if I think it is wise because a wise man does it, I then make the pure hypothesis that he does it because he is wise, and I reason à posteriori.

(Peirce, CE 1, 180).

Suppose we make the following assignments.

$\begin{array}{lll} \mathrm{A} & = & \text{Wisdom} \\ \mathrm{B} & = & \text{a certain character} \\ \mathrm{C} & = & \text{a certain conduct} \\ \mathrm{D} & = & \text{done by a wise man} \\ \mathrm{E} & = & \text{a certain occasion} \end{array}$

Recognizing a little more concreteness will aid understanding, let us make the following substitutions in Peirce’s example.

$\begin{array}{lllll} \mathrm{B} & = & \text{Benevolence} & = & \text{a certain character} \\ \mathrm{C} & = & \text{Contributes to Charity} & = & \text{a certain conduct} \\ \mathrm{E} & = & \text{Earlier today} & = & \text{a certain occasion} \end{array}$

The converging operation of all three reasonings is shown in Figure 2.

$\text{Figure 2. A Triply Wise Act}$

The common proposition concluding each argument is AC, contributing to charity is wise.

Deduction could have obtained the Fact AC from the Rule AB, benevolence is wisdom, along with the Case BC, contributing to charity is benevolent.
Induction could have gathered the Rule AC, contributing to charity is exemplary of wisdom, from the Fact AE, the act of earlier today is wise, along with the Case CE, the act of earlier today was an instance of contributing to charity.
Abduction could have guessed the Case AC, contributing to charity is explained by wisdom, from the Fact DC, contributing to charity is done by this wise man, and the Rule DA, everything wise is done by this wise man. Thus, a wise man, who does all the wise things there are to do, may nonetheless contribute to charity for no good reason and even be charitable to a fault. But on seeing the wise man contribute to charity it is natural to think charity may well be the mark of his wisdom, in essence, that wisdom is the reason he contributes to charity.

Resources

Logic Syllabus
Boolean Function
Boolean-Valued Function
Logical Conjunction
Minimal Negation Operator
Functional Logic • Part 1 • Part 2 • Part 3
Cactus Language • Part 1 • Part 2 • Part 3 • References • Document History

cc: FB | Peirce Matters • Laws of Form • Mathstodon • Ontolog • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Functional Logic • Inquiry and Analogy • 1

Posted on June 21, 2023 by Jon Awbrey

Inquiry and Analogy • Three Types of Reasoning

Types of Reasoning in Aristotle

Figure 1 gives a quick overview of traditional terminology I’ll have occasion to refer to as discussion proceeds.

$\text{Figure 1. Types of Reasoning in Aristotle}$

Resources

Logic Syllabus
Boolean Function
Boolean-Valued Function
Logical Conjunction
Minimal Negation Operator
Functional Logic • Part 1 • Part 2 • Part 3
Cactus Language • Part 1 • Part 2 • Part 3 • References • Document History

cc: FB | Peirce Matters • Laws of Form • Mathstodon • Ontolog • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Functional Logic • Inquiry and Analogy • Preliminaries

Posted on June 20, 2023 by Jon Awbrey

Functional Logic • Inquiry and Analogy

This report discusses C.S. Peirce’s treatment of analogy, placing it in relation to his overall theory of inquiry. We begin by introducing three basic types of reasoning Peirce adopted from classical logic. In Peirce’s analysis both inquiry and analogy are complex programs of logical inference which develop through stages of these three types, though normally in different orders.

Note on notation. The discussion to follow uses logical conjunctions, expressed in the form of concatenated tuples $e_1 ~\ldots~ e_k,$ and minimal negation operations, expressed in the form of bracketed tuples $\texttt{(} e_1 \texttt{,} \ldots \texttt{,} e_k \texttt{)},$ as the principal expression-forming operations of a calculus for boolean-valued functions, that is, for propositions. The expressions of this calculus parse into data structures whose underlying graphs are called cacti by graph theorists. Hence the name cactus language for this dialect of propositional calculus.

Resources

Logic Syllabus
Boolean Function
Boolean-Valued Function
Logical Conjunction
Minimal Negation Operator
Functional Logic • Part 1 • Part 2 • Part 3
Cactus Language • Part 1 • Part 2 • Part 3 • References • Document History

cc: FB | Peirce Matters • Laws of Form • Mathstodon • Ontolog • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science

Systems of Interpretation • 9

Posted on June 17, 2023 by Jon Awbrey

$\text{Figure 2. An Elementary Sign Relation}$

Re: Peirce List • Jerry Chandler

It is above all important to understand that Peirce’s concept of a sign relation is defined at a higher order of abstraction than any notion of causal or temporal order.

A sign relation $L \subseteq O \times S \times I$ is a structure which can generate the temporal sequences of signs making up a semiotic process but there is no necessary temporal order associated with the relational domains $O, S, I$ nor with the roles of objects, signs, and interpretant signs in any triple of the form $(o, s, i).$

As it happens, generative relationships between a generating structure and a generated class of structures are very common throughout mathematics and not unique to semiotics.

References

Awbrey, S.M., and Awbrey, J.L. (2001), “Conceptual Barriers to Creating Integrative Universities”, Organization : The Interdisciplinary Journal of Organization, Theory, and Society 8(2), Sage Publications, London, UK, 269–284. Abstract. Online.
Awbrey, S.M., and Awbrey, J.L. (September 1999), “Organizations of Learning or Learning Organizations : The Challenge of Creating Integrative Universities for the Next Century”, Second International Conference of the Journal ‘Organization’, Re‑Organizing Knowledge, Trans‑Forming Institutions : Knowing, Knowledge, and the University in the 21st Century, University of Massachusetts, Amherst, MA. Online.
Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), 40–52. Archive. Journal. Online (doc) (pdf).

cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science
cc: FB | Semeiotics • Mathstodon • Laws of Form • Academia.edu

Posted in C.S. Peirce, Diagrammatic Reasoning, Interpretive Frameworks, Logic, Logical Graphs, Objective Frameworks, Relation Theory, Semiotics, Sign Relations, Systems of Interpretation, Triadic Relations, Visualization | Tagged C.S. Peirce, Diagrammatic Reasoning, Interpretive Frameworks, Logic, Logical Graphs, Objective Frameworks, Relation Theory, Semiotics, Sign Relations, Systems of Interpretation, Triadic Relations, Visualization | 6 Comments

Systems of Interpretation • 8

Posted on June 16, 2023 by Jon Awbrey

$\text{Figure 3. Aspects of a Sign Relation}$

Re: Peirce List • Kirsti Määttänen

One of the chief advantages of Peirce’s systems of logical graphs, entitative and existential, is the way they escape the bounds of 1‑dimensional syntax and thus make it clear that many constraints of order imposed by the ordinary lines of linguistic text are not of the essence for logic but purely rhetorical accidents. That does, of course, leave open the question of what constraints imposed by the 2‑dimensional medium of Peirce’s logical graphs might also be inessential to logic.

As far as visualizations of sign relations go, without worrying about their use as a calculus, there is the above 3‑dimensional example from a paper Susan Awbrey and I presented at conference in 1999 and revised for publication in 2001.

Resources

References

Awbrey, S.M., and Awbrey, J.L. (2001), “Conceptual Barriers to Creating Integrative Universities”, Organization : The Interdisciplinary Journal of Organization, Theory, and Society 8(2), Sage Publications, London, UK, 269–284. Abstract. Online.
Awbrey, S.M., and Awbrey, J.L. (September 1999), “Organizations of Learning or Learning Organizations : The Challenge of Creating Integrative Universities for the Next Century”, Second International Conference of the Journal ‘Organization’, Re‑Organizing Knowledge, Trans‑Forming Institutions : Knowing, Knowledge, and the University in the 21st Century, University of Massachusetts, Amherst, MA. Online.
Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), 40–52. Archive. Journal. Online (doc) (pdf).

cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science
cc: FB | Semeiotics • Mathstodon • Laws of Form • Academia.edu

Systems of Interpretation • 7

Posted on June 15, 2023 by Jon Awbrey

$\text{Figure 2. An Elementary Sign Relation}$

Re: Peirce List • Gary Fuhrman

Peirce’s existential graphs are a general calculus for expressing the same subject matter as his logic of relative terms and thus they serve to represent the structures of many‑place relations. Cast at that level of generality, there is nothing to prevent existential graphs from being used to express the special cases of relative terms needed for a theory of triadic sign relations, for example, terms like “s stands to i for o” or “__ stands to __ for __” or any number of other forms, depending on the style one prefers. It may give us pause that we have to use sign relations in order to mention sign relations but the fact is we do that all the time whether we are using Peirce’s semiotics or not. Peirce’s pragmatic analysis of the process simply provides a clearer account than most other approaches do.

References

Awbrey, S.M., and Awbrey, J.L. (2001), “Conceptual Barriers to Creating Integrative Universities”, Organization : The Interdisciplinary Journal of Organization, Theory, and Society 8(2), Sage Publications, London, UK, 269–284. Abstract. Online.
Awbrey, S.M., and Awbrey, J.L. (September 1999), “Organizations of Learning or Learning Organizations : The Challenge of Creating Integrative Universities for the Next Century”, Second International Conference of the Journal ‘Organization’, Re‑Organizing Knowledge, Trans‑Forming Institutions : Knowing, Knowledge, and the University in the 21st Century, University of Massachusetts, Amherst, MA. Online.
Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), 40–52. Archive. Journal. Online (doc) (pdf).

cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science
cc: FB | Semeiotics • Mathstodon • Laws of Form • Academia.edu

Systems of Interpretation • 6

Posted on June 14, 2023 by Jon Awbrey

$\text{Figure 2. An Elementary Sign Relation}$

Re: Peirce List • Jon Awbrey • John Collier

JA:: Questions about the meaning of the “central hub” in the “three‑spoked” picture of an elementary sign relation have often come up. The central “spot”, as Peirce called it in his logical graphs, is located on a different logical plane, since it is really a place‑holder for the whole sign relation or possibly for the individual triple. Normally I would have labeled it with a letter to indicate the whole sign relation, say $L,$ or else the individual triple, say $\ell = (o, s, i).$

JC:: I strongly agree, Jon. Reading meaning into artefacts of the representation is not typically transparent. I would say that the whole symbol represents the sign with its threefold character and that the node is not some separate signifier. To put it on this level is, as you suggest, a category error.

Precisely. And “artefact” is a very choice word here, with all the right connotations. It would be unfortunate if this trivial “triskelion” figure became a caltrop to our thought, blocking the way of inquiry.

Aside from the ellipses we added to call attention to a couple of derivative dyadic relations, somewhat loosely called denotative and connotative in our paper, it is merely typical of the 3‑spoke figures in common use when I was first learning Peirce’s theory of signs, often arising to point out the differences between Saussure’s dyadic semiology and Peirce’s triadic semiotics.

The intervening decades have taught me all the ways diagrams and figures of that sort can be misinterpreted when the conventions of interpretation needed to understand them are not up and running. It can be instructive to carry out post mortems on the various maps of misreading but if one is not up for the morbidity of that, it is probably wiser to move on to more viable representations.

References

Awbrey, S.M., and Awbrey, J.L. (2001), “Conceptual Barriers to Creating Integrative Universities”, Organization : The Interdisciplinary Journal of Organization, Theory, and Society 8(2), Sage Publications, London, UK, 269–284. Abstract. Online.
Awbrey, S.M., and Awbrey, J.L. (September 1999), “Organizations of Learning or Learning Organizations : The Challenge of Creating Integrative Universities for the Next Century”, Second International Conference of the Journal ‘Organization’, Re‑Organizing Knowledge, Trans‑Forming Institutions : Knowing, Knowledge, and the University in the 21st Century, University of Massachusetts, Amherst, MA. Online.
Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), 40–52. Archive. Journal. Online (doc) (pdf).

cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science
cc: FB | Semeiotics • Mathstodon • Laws of Form • Academia.edu

Systems of Interpretation • Discussion 1

Posted on June 12, 2023 by Jon Awbrey

Re: FB | Systems Sciences • Esteban Trev

ET:: What is the difference between sign and symbol?

In Peirce’s usage, “sign” is the generic term, covering all species or types of signs. Signs are “symbolic” to the extent they mean what they do solely by virtue of being interpreted to do so. In Peirce’s fully triadic semiotics all signs are symbolic to some degree, even when they have the additional properties required to qualify them as “icons”, “indices”, or more specialized types.

Resources

Semeiotic • Inquiry Blog • OEIS Wiki
Survey of Semiotics, Semiosis, Sign Relations

cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science
cc: FB | Semeiotics • Mathstodon • Laws of Form • Academia.edu

	Survey of Differenti… on Differential Logic • 9
	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…
	Differential Logic •… on Logic Syllabus
	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…
	Differential Logic •… on Logic Syllabus
	Survey of Differenti… on Differential Logic • 8
	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…

Inquiry and Analogy • Aristotle’s “Apagogy” • Abductive Reasoning

Resources

Share this:

Inquiry and Analogy • Comparison of the Analyses

Resources

Share this:

Inquiry and Analogy • Three Types of Reasoning

Resources

Share this:

Inquiry and Analogy • Three Types of Reasoning

Resources

Share this:

Resources

Share this:

References

Share this:

Resources

References

Share this:

References

Share this:

References

Share this:

Resources

Share this:

Elsewhere

Blogroll

Follow Blog via Email

Recent Posts

Recent Comments

Archives

Blog Stats

Categories

Logic, Mathematics, Philosophy

Current Events

Meta