Re: Gil Kalai • Why Is Mathematics Possible? • Tim Gowers’ Take On The Matter
Comment 1
To the extent that mathematics has to do with reasoning about possible existence, or inference from pure hypothesis, a line of thinking going back to Aristotle and developed greatly by C.S. Peirce may have some bearing on the question of “Why Mathematics Is Possible”. In that line of thought, hypothesis formation is treated as a case of “abductive” inference, whose job in science generally is to supply suitable raw materials for deduction and induction to develop and test. In that light, a large part of our original question becomes, as Peirce once expressed it —
Is there cause to believe “we can trust to the human mind’s having such a power of guessing right that before very many hypotheses shall have been tried, intelligent guessing may be expected to lead us to the one which will support all tests, leaving the vast majority of possible hypotheses unexamined”? (Peirce, Collected Papers, CP 6.530).
The question may fit the situation in mathematics slightly better if we modify the word “hypothesis” to say “proof“.
Comment 2
I copied out a more substantial excerpt from Peirce’s paper here:
The question of naturalness arises in many areas, from AI and cognitive science to logic and the philosophy of science, most often under the heading of “Natural Kinds”. Given a universe of discourse 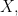 the lattice of “All Kinds” would be its power set, and we want to know what portion of that ordering makes up the Natural Kinds, the concepts or hypotheses that are worth considering in practice.
the lattice of “All Kinds” would be its power set, and we want to know what portion of that ordering makes up the Natural Kinds, the concepts or hypotheses that are worth considering in practice.
To the same purpose, Peirce employs the criterion of “admissible hypotheses that seem the simplest to the human mind”.
Comment 3
The following project report outlines the three types of inference — Abductive, Deductive, and Inductive — as treated by Aristotle and Peirce, at least insofar as these patterns of reasoning can be analyzed in syllogistic forms. I did this work by way of exploring how a propositional logic engine might be used to assist in scientific inquiry.
It looks a bit cobbled together to my eyes today and probably could use a rewrite, but I did put a lot of work into the diagrams and remain rather pleased with those.
References
Well, more like allusions, really …
- McCulloch, Warren S. (1961), “What Is a Number that a Man May Know It, and a Man, that He May Know a Number?”, Ninth Alfred Korzybski Memorial Lecture, General Semantics Bulletin, Numbers 26 and 27, pp. 7–18, Institute of General Semantics, Lakeville, CT. Reprinted in Embodiments of Mind, pp. 1–18. Online (1) (2).
- McCulloch, Warren S. (1965), Embodiments of Mind, MIT Press, Cambridge, MA.
