Inquiry Into Inquiry

Re: Peirce List • Jon Awbrey • John Collier

JA:

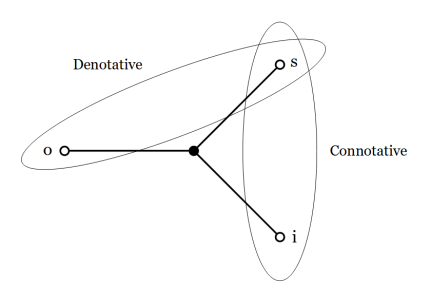
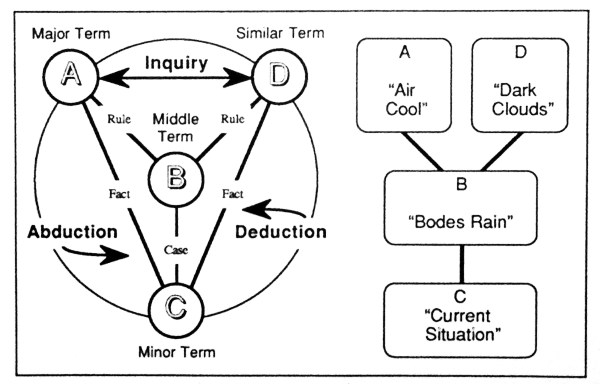
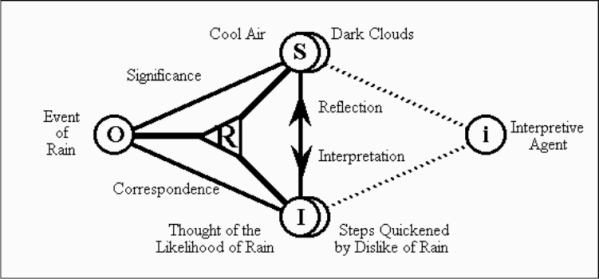
Questions about the meaning of the “central hub” in the “three‑spoked” picture of an elementary sign relation have often come up.  The central “spot”, as Peirce called it in his logical graphs, is located on a different logical plane, since it is really a place‑holder for the whole sign relation or possibly for the individual triple.  Normally I would have labeled it with a letter to indicate the whole sign relation, say or else the individual triple, say

JC:

I strongly agree, Jon.  Reading meaning into artefacts of the representation is not typically transparent.  I would say that the whole symbol represents the sign with its threefold character and that the node is not some separate signifier.  To put it on this level is, as you suggest, a category error.

Precisely.  And “artefact” is a very choice word here, with all the right connotations.  It would be unfortunate if this trivial “triskelion” figure became a caltrop to our thought, blocking the way of inquiry.

Aside from the ellipses we added to call attention to a couple of derivative dyadic relations, somewhat loosely called denotative and connotative in our paper, it is merely typical of the 3‑spoke figures in common use when I was first learning Peirce’s theory of signs, often arising to point out the differences between Saussure’s dyadic semiology and Peirce’s triadic semiotics.

The intervening decades have taught me all the ways diagrams and figures of that sort can be misinterpreted when the conventions of interpretation needed to understand them are not up and running.  It can be instructive to carry out post mortems on the various maps of misreading but if one is not up for the morbidity of that, it is probably wiser to move on to more viable representations.

References

• Awbrey, S.M., and Awbrey, J.L. (2001), “Conceptual Barriers to Creating Integrative Universities”, Organization : The Interdisciplinary Journal of Organization, Theory, and Society 8(2), Sage Publications, London, UK, 269–284.  Abstract.  Online.
• Awbrey, S.M., and Awbrey, J.L. (September 1999), “Organizations of Learning or Learning Organizations : The Challenge of Creating Integrative Universities for the Next Century”, Second International Conference of the Journal ‘Organization’, Re‑Organizing Knowledge, Trans‑Forming Institutions : Knowing, Knowledge, and the University in the 21st Century, University of Massachusetts, Amherst, MA.  Online.
• Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), 40–52.  Archive.  Journal.  Online (doc) (pdf).

cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science
cc: FB | Semeiotics • Mathstodon • Laws of Form • Peirce List (1) (2) (3) (4) (5)

Re: Peirce List • Jerry Chandler

An elementary sign relation is an ordered triple   It is called elementary because it is one element of a sign relation where is a set of objects, is a set of signs, and is a set of interpretant signs that are collectively called the domains of the relation.

But what is the significance of that ordering?

In any presentation of subject matter we have to distinguish the natural order of things from the order of consideration or presentation in which things are taken up on a given occasion.

The natural order of things comes to light through the discovery of invariants over a variety of presentations and representations.  That type of order tends to take a considerable effort to reveal.

The order of consideration or presentation is often more arbitrary, making some aspects of the subject matter more salient than others depending on the paradigm or perspective one has chosen.

In the case of sign relations, the order in which we take up the domains or the components of a triple is wholly arbitrary so long as we maintain the same order throughout the course of discussion.

References

• Awbrey, S.M., and Awbrey, J.L. (2001), “Conceptual Barriers to Creating Integrative Universities”, Organization : The Interdisciplinary Journal of Organization, Theory, and Society 8(2), Sage Publications, London, UK, 269–284.  Abstract.  Online.
• Awbrey, S.M., and Awbrey, J.L. (September 1999), “Organizations of Learning or Learning Organizations : The Challenge of Creating Integrative Universities for the Next Century”, Second International Conference of the Journal ‘Organization’, Re‑Organizing Knowledge, Trans‑Forming Institutions : Knowing, Knowledge, and the University in the 21st Century, University of Massachusetts, Amherst, MA.  Online.
• Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), 40–52.  Archive.  Journal.  Online (doc) (pdf).

cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science
cc: FB | Semeiotics • Mathstodon • Laws of Form • Peirce List (1) (2) (3) (4) (5)

Re: Peirce List • Mike Bergman • Valentine Daniel

For its pertinence to the present discussion, here again is what Peirce wrote about the mathematical way of using individual or particular cases to make general hypotheses or suppositions:

• Mathematical Demonstration and the Doctrine of Individuals • 1

And just so we don’t forget that Peirce’s theory of individuals is not the run-of-the-mill absolute kind but makes the quality of individuality relative to the context of discussion — or the frame of reference as they say in physics — here is what he wrote about that:

• Mathematical Demonstration and the Doctrine of Individuals • 2

cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science
cc: FB | Semeiotics • Mathstodon • Laws of Form • Peirce List (1) (2) (3) (4) (5)

Re: Peirce List • Mike Bergman • Valentine Daniel

The “triskelion” figure in the previous post shows the bare essentials of an elementary sign relation or individual triple   There’s a less skeletal figure Susan Awbrey and I used in an earlier paper, where our aim was to articulate the commonalities Peirce’s concept of a sign relation shares with its archetype in Aristotle.

Here is the corresponding passage from “On Interpretation”.

Words spoken are symbols or signs (symbola) of affections or impressions (pathemata) of the soul (psyche);  written words are the signs of words spoken.  As writing, so also is speech not the same for all races of men.  But the mental affections themselves, of which these words are primarily signs (semeia), are the same for the whole of mankind, as are also the objects (pragmata) of which those affections are representations or likenesses, images, copies (homoiomata).  (De Interp. i. 16^a4).

References

• Awbrey, J.L., and Awbrey, S.M. (1995), “Interpretation as Action : The Risk of Inquiry”, Inquiry : Critical Thinking Across the Disciplines 15(1), 40–52.  Archive.  Journal.  Online (doc) (pdf).
• Awbrey, S.M., and Awbrey, J.L. (2001), “Conceptual Barriers to Creating Integrative Universities”, Organization : The Interdisciplinary Journal of Organization, Theory, and Society 8(2), Sage Publications, London, UK, 269–284.  Abstract.  Online.
• Awbrey, S.M., and Awbrey, J.L. (September 1999), “Organizations of Learning or Learning Organizations : The Challenge of Creating Integrative Universities for the Next Century”, Second International Conference of the Journal ‘Organization’, Re‑Organizing Knowledge, Trans‑Forming Institutions : Knowing, Knowledge, and the University in the 21st Century, University of Massachusetts, Amherst, MA.  Online.

cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science
cc: FB | Semeiotics • Mathstodon • Laws of Form • Peirce List (1) (2) (3) (4) (5)

Re: Peirce List • Mike Bergman • Valentine Daniel

Let’s start as simply as possible.  The following Figure is typical of many I have used to illustrate sign relations from the time I first began studying Peirce’s theory of signs.

The above variant comes from a paper Susan Awbrey and I presented at a conference in 1999, a revised version of which was published in 2001.

As the drafter of that drawing I can speak with authority about the artist’s intentions in drawing it and also about the conventions of interpretation forming the matrix of its conception and delivery.

Just by way of refreshing my own memory, here is how we set it up —

Figure 2 represents an “elementary sign relation”.  It is a single transaction taking place among three entities, the object the sign and the interpretant sign the association of which is typically represented by means of the ordered triple

One of the interpretive conventions implied in that setup is hallowed by long tradition, going back to the earliest styles of presentation in mathematics.  In it one draws a figure intended as “representative” of many figures.  Regarded as a concrete drawing the figure is naturally imperfect, individual, peculiar, and special but it’s meant to be taken purely as a representative of its class — generic, ideal, and typical.  That is the main convention of interpretation which goes into giving diagrams and figures their significant power.

References

• Awbrey, S.M., and Awbrey, J.L. (2001), “Conceptual Barriers to Creating Integrative Universities”, Organization : The Interdisciplinary Journal of Organization, Theory, and Society 8(2), Sage Publications, London, UK, 269–284.  Abstract.  Online.
• Awbrey, S.M., and Awbrey, J.L. (September 1999), “Organizations of Learning or Learning Organizations : The Challenge of Creating Integrative Universities for the Next Century”, Second International Conference of the Journal ‘Organization’, Re‑Organizing Knowledge, Trans‑Forming Institutions : Knowing, Knowledge, and the University in the 21st Century, University of Massachusetts, Amherst, MA.  Online.

cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science
cc: FB | Semeiotics • Mathstodon • Laws of Form • Peirce List (1) (2) (3) (4) (5)

Re: Peirce List • Mike Bergman • Valentine Daniel

Questions have arisen about the different styles of diagrams and figures used to represent triadic sign relations in Peircean semiotics.  What do they mean?  Which style is best?  Among the most popular pictures some use geometric triangles while others use the three‑pronged graphs Peirce used in his logical graphs to represent triadic relations.

Diagrams and figures, like any signs, can serve to communicate the intended interpretants and thus to coordinate the conduct of interpreters toward the intended objects — but only in communities of interpretation where the conventions of interpretation are understood.  Conventions of interpretation are by comparison far more difficult to communicate.

That brings us to the first question we have to ask about the possibility of communication in this area, namely, what conventions of interpretation are needed to make sense of these diagrams, figures, and graphs?

cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science
cc: FB | Semeiotics • Mathstodon • Laws of Form • Peirce List (1) (2) (3) (4) (5)