Re: Peirce List (1) (2)
Re: Jerry Rhee, quoting Peirce (1) (2)
The surprising fact, C, is observed;
But if A were true, C would be a matter of course,
Hence, there is reason to suspect that A is true. (CP 5.189)
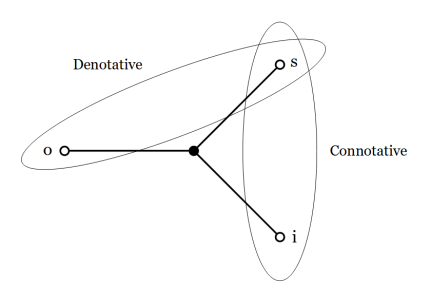
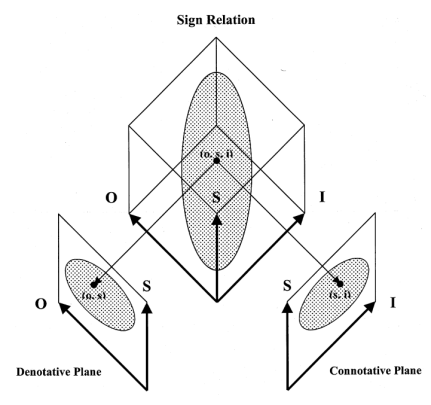
For now I’m just focused on the bare essentials of Peirce’s semiotics, specifically, the minimal adequate definition of a sign relation as it figures into Peirce’s definition of logic along with the necessary concepts of triple correspondence and triadic determination on which all the rest depends.
The essential definitions of logic and sign relations can be found on the following page.
It would take a while to get from there to his full theory of inquiry, involving the interplay of abductive, deductive, and inductive styles of inference, but first things first, as they say.
Just as a side note, though, I’m sure every writer who ever attempted to introduce a complex subject to a new audience has tried the tactic of seeking out the simplest possible capsule summary of its main gist. The pithy epitome of abduction cited above is a perfect example of just such a capsule and I have seen vast literatures in several areas spring from its pith and moment only to have their currents turn awry from its oversimplifications. Let’s not get addicted to that capsule!
A better idea of the rich interplay among the three styles of reasoning and how they work in tandem to reinforce one another in genuine inquiry may be had from the study I carried out when I was working to view Peirce’s theories of inference, information, and inquiry from a systems analysis perspective on a systems engineering platform. There is a sketch of that work in the following report.
cc: Inquiry List • Peirce List (1) (2) (3) (4) (5)