Inquiry Into Inquiry

Note.  This is a placeholder, to be developed later.

Figure 2 shows the implication ordering of logical terms in the form of a lattice diagram.

Figure 2. Disjunctive Term u, Taken as Subject

Reference

• Peirce, C.S. (1866), “The Logic of Science, or, Induction and Hypothesis”, Lowell Lectures of 1866, pp. 357–504 in Writings of Charles S. Peirce : A Chronological Edition, Volume 1, 1857–1866, Peirce Edition Project, Indiana University Press, Bloomington, IN, 1982.

Resources

• C.S. Peirce • Upon Logical Comprehension and Extension
• My Notes • Information = Comprehension × Extension

Let’s stay with Peirce’s example of abductive inference a little longer and try to clear up the more troublesome confusions tending to arise.

Figure 1 shows the implication ordering of logical terms in the form of a lattice diagram.

Figure 1. Conjunctive Term z, Taken as Predicate

One thing needs to be stressed at this point.  It is important to recognize the conjunctive term itself — namely, the syntactic string “spherical bright fragrant juicy tropical fruit” — is not an icon but a symbol.  It has its place in a formal system of symbols, for example, a propositional calculus, where it would normally be interpreted as a logical conjunction of six elementary propositions, denoting anything in the universe of discourse having all six of the corresponding properties.  The symbol denotes objects which may be taken as icons of oranges by virtue of bearing those six properties.  But there are no objects denoted by the symbol which aren’t already oranges themselves.  Thus we observe a natural reduction in the denotation of the symbol, consisting in the absence of cases outside of oranges that have all the properties indicated.

The above analysis provides another way to understand the abductive inference from the Fact and the Rule to the Case   The lack of any cases which are and not is expressed by the implication   Taking this together with the Rule gives the logical equivalence   But this reduces the Case to the Fact and so the Case is justified.

Viewed in the light of the above analysis, Peirce’s example of abductive reasoning exhibits an especially strong form of inference, almost deductive in character.  Do all abductive arguments take this form, or may there be weaker styles of abductive reasoning which enjoy their own levels of plausibility?  That must remain an open question at this point.

Reference

• Peirce, C.S. (1866), “The Logic of Science, or, Induction and Hypothesis”, Lowell Lectures of 1866, pp. 357–504 in Writings of Charles S. Peirce : A Chronological Edition, Volume 1, 1857–1866, Peirce Edition Project, Indiana University Press, Bloomington, IN, 1982.

Resources

• C.S. Peirce • Upon Logical Comprehension and Extension
• My Notes • Information = Comprehension × Extension

Many things still puzzle me about Peirce’s account at this point.  I indicated a few of them by means of question marks at several places in the last two Figures.  There is nothing for it but returning to the text and trying once more to follow the reasoning.

Let’s go back to Peirce’s example of abductive inference and try to get a clearer picture of why he connects it with conjunctive terms and iconic signs.

Figure 1 shows the implication ordering of logical terms in the form of a lattice diagram.

Figure 1. Conjunctive Term z, Taken as Predicate

The relationship between conjunctive terms and iconic signs may be understood as follows.  If there is anything having all the properties described by the conjunctive term — spherical bright fragrant juicy tropical fruit — then sign users may use that thing as an icon of an orange, precisely by virtue of the fact it shares those properties with an orange.  But the only natural examples of things with all those properties are oranges themselves, so the only thing able to serve as a natural icon of an orange by virtue of those properties is that orange itself or another orange.

Reference

• Peirce, C.S. (1866), “The Logic of Science, or, Induction and Hypothesis”, Lowell Lectures of 1866, pp. 357–504 in Writings of Charles S. Peirce : A Chronological Edition, Volume 1, 1857–1866, Peirce Edition Project, Indiana University Press, Bloomington, IN, 1982.

Resources

• C.S. Peirce • Upon Logical Comprehension and Extension
• My Notes • Information = Comprehension × Extension

Peirce identifies inference with a process he describes as symbolization.  Let us consider what that might imply.

I am going, next, to show that inference is symbolization and that the puzzle of the validity of scientific inference lies merely in this superfluous comprehension and is therefore entirely removed by a consideration of the laws of information.  (467).

Even if it were only a weaker analogy between inference and symbolization, a principle of logical continuity — what in physics is called a correspondence principle — would suggest parallels between steps of reasoning in the neighborhood of exact inferences and signs in the vicinity of genuine symbols.  This would lead us to expect a correspondence between degrees of inference and degrees of symbolization that extends from exact to approximate or non-demonstrative inferences and from genuine to approximate or degenerate symbols.

In addition to Aristotle, the influence of Kant on Peirce is very strongly marked in these earliest expositions.  The invocations of “conceptions of the understanding”, the “use of concepts” and thus of symbols in reducing the manifold of extension, and the not so subtle hint of the synthetic à priori in Peirce’s discussion, not only of natural kinds but also of the kinds of signs leading up to genuine symbols, can all be recognized as pervasive Kantian themes.

In order to draw out these themes and see how Peirce was led to develop their leading ideas, let us bring together our previous Figures, abstracting from their concrete details, and see if we can figure out what is going on here.

Figure 3 shows an abductive step of inquiry, as taken on the cue of an iconic sign.

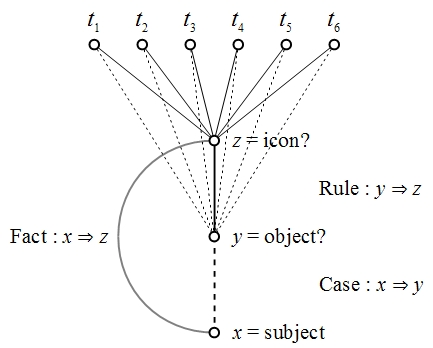
Figure 3. Conjunctive Predicate z, Abduction of Case x ⇒ y

Figure 4 shows an inductive step of inquiry, as taken on the cue of an indicial sign.

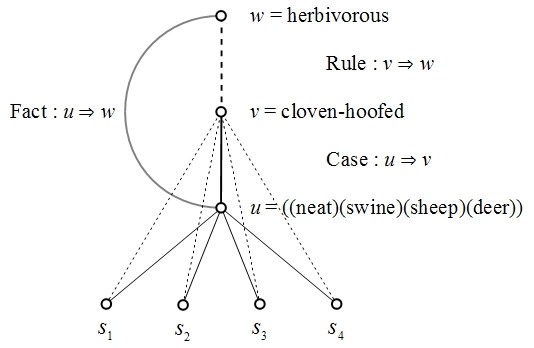
Figure 4. Disjunctive Subject u, Induction of Rule v ⇒ w

To be continued …

Reference

• Peirce, C.S. (1866), “The Logic of Science, or, Induction and Hypothesis”, Lowell Lectures of 1866, pp. 357–504 in Writings of Charles S. Peirce : A Chronological Edition, Volume 1, 1857–1866, Peirce Edition Project, Indiana University Press, Bloomington, IN, 1982.

Resources

• C.S. Peirce • Upon Logical Comprehension and Extension
• My Notes • Information = Comprehension × Extension