Animated Logical Graphs • 22

Posted on July 22, 2019 by Jon Awbrey

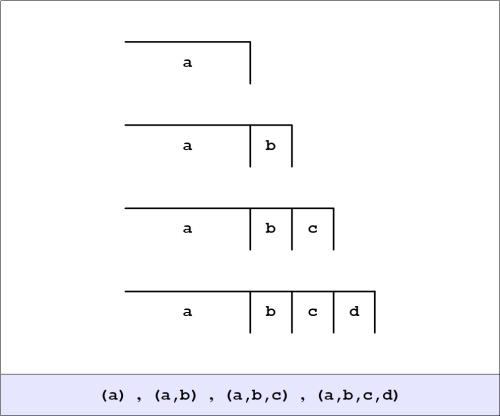
The step of controlled reflection we took with the previous post can be repeated at will, as suggested by the following series of forms.

Reflective Series (a) to (a, b, c, d)

Written inline, we have the series {}^{\backprime\backprime} \texttt{(} a \texttt{)} {}^{\prime\prime}, {}^{\backprime\backprime} \texttt{(} a \texttt{,} b \texttt{)} {}^{\prime\prime}, {}^{\backprime\backprime} \texttt{(} a \texttt{,} b \texttt{,} c \texttt{)} {}^{\prime\prime}, {}^{\backprime\backprime} \texttt{(} a \texttt{,} b \texttt{,} c \texttt{,} d \texttt{)} {}^{\prime\prime}, and so on, whose general form is {}^{\backprime\backprime} \texttt{(} x_1 \texttt{,} x_2 \texttt{,} \ldots \texttt{,} x_k \texttt{)} {}^{\prime\prime}.  With this move we have passed beyond the graph-theoretical form of rooted trees to what graph theorists know as rooted cacti.

I will discuss this cactus language and its logical interpretations next.

cc: Cybernetics (1) (2) • Peirce (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) (14)
cc: Ontolog Forum (1) (2) • Structural Modeling (1) (2) • Systems Science (1) (2)
cc: FB | Logical Graphs • Laws of Form

This entry was posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization and tagged , , , , , , , , , , , , , , , , , , , , , , , , , . Bookmark the permalink.