Examples from Semiotics

The study of signs — the full variety of significant forms of expression — in relation to all the affairs signs are significant of, and in relation to all the beings signs are significant to, is known as semiotics or the theory of signs.  As described, semiotics treats of a 3-place relation among signs, their objects, and their interpreters.

The term semiosis refers to any activity or process involving signs.  Studies of semiosis focusing on its abstract form are not concerned with every concrete detail of the entities acting as signs, as objects, or as agents of semiosis, but only with the most salient patterns of relationship among those three roles.  In particular, the formal theory of signs does not consider all the properties of the interpretive agent but only the more striking features of the impressions signs make on a representative interpreter.  From a formal point of view this impact or influence may be treated as just another sign, called the interpretant sign, or the interpretant for short.  A triadic relation of this type, among objects, signs, and interpretants, is called a sign relation.

For example, consider the aspects of sign use involved when two people, say Ann and Bob, use their own proper names, “Ann” and “Bob”, along with the pronouns, “I” and “you”, to refer to themselves and each other.  For brevity, these four signs may be abbreviated to the set   The abstract consideration of how and use this set of signs leads to the contemplation of a pair of triadic relations, the sign relations and reflecting the differential use of these signs by and respectively.

Each of the sign relations and consists of eight triples of the form where the object belongs to the object domain the sign belongs to the sign domain the interpretant sign belongs to the interpretant domain and where it happens in this case that   The union is often referred to as the syntactic domain, but in this case

The set-up so far is summarized as follows:

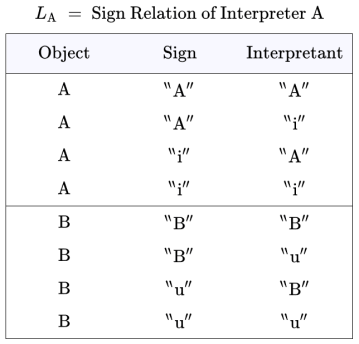
The relation is the following set of eight triples in

The triples in represent the way interpreter uses signs.  For example, the presence of in says uses to mean the same thing uses to mean, namely,

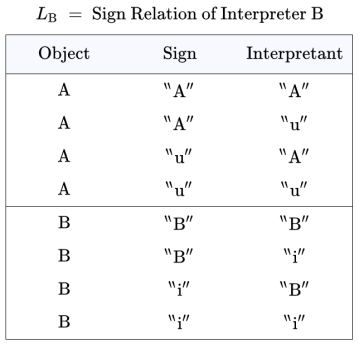
The relation is the following set of eight triples in

The triples in represent the way interpreter uses signs.  For example, the presence of in says uses to mean the same thing uses to mean, namely,

The triples in the relations and are conveniently arranged in the form of relational data tables, as shown below.

Resources

• Logic Syllabus
• Sign Relations
• Triadic Relations
• Relation Theory

Document History

Portions of the above article were adapted from the following sources under the GNU Free Documentation License, under other applicable licenses, or by permission of the copyright holders.

• Triadic Relation • OEIS Wiki
• Triadic Relation • InterSciWiki
• Triadic Relation • MyWikiBiz
• Triadic Relation • Wikiversity
• Triadic Relation • Wikipedia

cc: Cybernetics • Ontolog Forum • Peirce List • Structural Modeling • Systems Science