Inquiry Into Inquiry

Animated Logical Graphs • 65

Posted on March 4, 2021 by Jon Awbrey

Thus, what looks to us like a sphere of scientific knowledge more accurately should be represented as the inside of a highly irregular and spiky object, like a pincushion or porcupine, with very sharp extensions in certain directions, and virtually no knowledge in immediately adjacent areas. If our intellectual gaze could shift slightly, it would alter each quill’s direction, and suddenly our entire reality would change.

Herbert J. Bernstein • “Idols of Modern Science”

Re: Laws of Form • Lyle Anderson
Re: Richard J. Lipton • The Art Of Math

Dear Lyle,

Thanks for the link to the Wikipedia article on Cactus Graphs, which I found surprisingly good for that venue. I was pleased to see it mentioned the role my own first teacher in graph theory, Frank Harary, played in the history of cactus graphs. Frank co-authored Graphical Enumeration and many papers with Ed Palmer, my second teacher in graph theory and later my advisor in grad school.

Synchronicity being what it is, one of the jobs I worked on between my undergrad decade and my first crack at grad school was scanning and measuring particle interactions on bubble-chamber filmstrips in a high-energy physics lab, so I got a gadshillion gammas engrammed in my brain from that time.

Regards,

Jon

Resources

cc: Cybernetics (1) (2) • Laws of Form • FB | Logical Graphs • Ontolog Forum (1) (2)
• Peirce List (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) (13) • Structural Modeling (1) (2)
• Systems Science (1) (2)

Posted in Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | Tagged Amphecks, Animata, Boolean Algebra, Boolean Functions, C.S. Peirce, Cactus Graphs, Constraint Satisfaction Problems, Deduction, Diagrammatic Reasoning, Duality, Equational Inference, Graph Theory, Laws of Form, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Model Theory, Painted Cacti, Peirce, Proof Theory, Propositional Calculus, Propositional Equation Reasoning Systems, Spencer Brown, Theorem Proving, Visualization | 15 Comments

Animated Logical Graphs • 64

Posted on March 4, 2021 by Jon Awbrey

If exegesis raised a hermeneutic problem, that is, a problem of interpretation, it is because every reading of a text always takes place within a community, a tradition, or a living current of thought, all of which display presuppositions and exigencies — regardless of how closely a reading may be tied to the quid, to “that in view of which” the text was written.

Paul Ricoeur • The Conflict of Interpretations

Re: Laws of Form • John Mingers
Re: Richard J. Lipton • The Art Of Math

Dear John,

It occurred to me a picture might save a few thousand words. A good place to start is the following Table from an earlier post on my blog.

The smart way to deal with parens + character strings in computing is to parse them into graph-theoretic data structures and then work on those instead of the strings themselves. Usually one gets some sort of tree structures for the parse graphs. In my work on logical graphs I eventually came to use the more general species of structure graph theorists call cactus graphs or cacti.

Referring to the Table —

Column 1 shows the logical graphs I use for the sixteen boolean functions on two variables, with the string forms underneath. The cactus string obtained by traversing the cactus graph uses parens + commas + variables in forms like $\texttt{(} x \texttt{,} y \texttt{)}$ and $\texttt{((} x \texttt{,} y \texttt{))}.$
Column 2 shows the venn diagram associated with the entitative interpretation of the graph in Column 1. This is the interpretation C.S. Peirce used in his earlier work on entitative graphs and the one Spencer Brown used in his Laws of Form.
Column 3 shows the venn diagram associated with the existential interpretation of the graph in Column 1. This is the interpretation C.S. Peirce used in his later work on existential graphs.

Logical Graphs • Entitative and Existential Venn Diagrams
$\text{Logical Graph}$	$\text{Entitative Interpretation}$	$\text{Existential Interpretation}$

$\texttt{(} ~ \texttt{)}$	$\text{true}$ $f_{15}$	$\text{false}$ $f_{0}$

$\texttt{(} x \texttt{)(} y \texttt{)}$	$\lnot x \lor \lnot y$ $f_{7}$	$\lnot x \land \lnot y$ $f_{1}$

$\texttt{(} x \texttt{)} y$	$x \Rightarrow y$ $f_{11}$	$x \nLeftarrow y$ $f_{2}$

$\texttt{(} x \texttt{)}$	$\lnot x$ $f_{3}$	$\lnot x$ $f_{3}$

$x \texttt{(} y \texttt{)}$	$x \Leftarrow y$ $f_{13}$	$x \nRightarrow y$ $f_{4}$

$\texttt{(} y \texttt{)}$	$\lnot y$ $f_{5}$	$\lnot y$ $f_{5}$

$\texttt{(} x \texttt{,} y \texttt{)}$	$x = y$ $f_{9}$	$x \ne y$ $f_{6}$

$\texttt{(} x y \texttt{)}$	$\lnot (x \lor y)$ $f_{1}$	$\lnot (x \land y)$ $f_{7}$

$x y$	$x \lor y$ $f_{14}$	$x \land y$ $f_{8}$

$\texttt{((} x \texttt{,} y \texttt{))}$	$x \ne y$ $f_{6}$	$x = y$ $f_{9}$

$y$	$y$ $f_{10}$	$y$ $f_{10}$

$\texttt{(} x \texttt{(} y \texttt{))}$	$x \nLeftarrow y$ $f_{2}$	$x \Rightarrow y$ $f_{11}$

$x$	$x$ $f_{12}$	$x$ $f_{12}$

$\texttt{((} x \texttt{)} y \texttt{)}$	$x \nRightarrow y$ $f_{4}$	$x \Leftarrow y$ $f_{13}$

$\texttt{((} x \texttt{)(} y \texttt{))}$	$x \land y$ $f_{8}$	$x \lor y$ $f_{14}$

	$\text{false}$ $f_{0}$	$\text{true}$ $f_{15}$

Take a gander at all that and I’ll discuss more tomorrow …

Regards,

Jon

Resources

Animated Logical Graphs • 63

Posted on March 2, 2021 by Jon Awbrey

Re: Richard J. Lipton • The Art Of Math
Re: Animated Logical Graphs • (57) • (58) • (59) • (60) • (61) • (62)

We’ve been using the duality between entitative and existential interpretations of logical graphs to get a handle on the mathematical forms pervading logical laws. A few posts ago we took up the tools of groups and symmetries and transformations to study the duality and we looked to the space of 2-variable boolean functions as a basic training grounds. On those grounds the translation between interpretations presents as a group $G$ of order two acting on a set $X$ of sixteen logical graphs denoting boolean functions.

Last time we arrived at a Table showing how the group $G$ partitions the set $X$ into ten orbits of logical graphs. Here again is that Table.

$\text{Peirce Duality as Group Symmetry} \stackrel{_\bullet}{} \text{Orbit Order}$

I invited the reader to investigate the relationship between the group order $|G| = 2,$ the number of orbits $10,$ and the total number of fixed points $16 + 4 = 20.$ In the present case the product of the group order (2) and the number of orbits (10) is equal to the sum of the fixed points (20) — Is that just a fluke? If not, why so? And does it reflect a general rule?

We can make a beginning toward answering those questions by inspecting the incidence relation of fixed points and orbits in the Table above. Each singleton orbit accumulates two hits, one from the group identity and one from the other group operation. But each doubleton orbit also accumulates two hits, since the group identity fixes both of its two points. Thus all the orbits are double-counted by counting the incidence of fixed points and orbits. In sum, dividing the total number of fixed points by the order of the group brings us back to the exact number of orbits.

Resources

Animated Logical Graphs • 62

Posted on February 28, 2021 by Jon Awbrey

Re: Richard J. Lipton • The Art Of Math
Re: Animated Logical Graphs • (57) • (58) • (59) • (60) • (61)

Another way of looking at the dual interpretation of logical graphs from a group-theoretic point of view is provided by the following Table. In this arrangement we have sorted the rows of the previous Table to bring together similar graphs $\gamma$ belonging to the set $X,$ the similarity being determined by the action of the group $G = \{ 1, t \}.$ Transformation group theorists refer to the corresponding similarity classes as orbits of the group action under consideration. The orbits are defined by the group acting transitively on them, meaning elements of the same orbit can always be transformed into one another by some group operation while elements of different orbits cannot.

$\text{Peirce Duality as Group Symmetry} \stackrel{_\bullet}{} \text{Orbit Order}$

Scanning the Table we observe the 16 points of $X$ fall into 10 orbits total, divided into 4 orbits of 1 point each and 6 orbits of 2 points each. The points in singleton orbits are called fixed points of the transformation group since they are not moved but mapped into themselves by all group actions. The bottom row of the Table tabulates the total number of fixed points for the group operations $1$ and $t$ respectively. The group identity $1$ always fixes all points, so its total is 16. The group action $t$ fixes only the four points in singleton orbits, giving a total of 4.

I leave it as an exercise for the reader to investigate the relationship between the group order $|G| = 2,$ the number of orbits $10,$ and the total number of fixed points $16 + 4 = 20.$

Resources

cc: Cybernetics (1) (2) • Laws of Form • FB | Logical Graphs • Ontolog Forum (1) (2)
• Peirce List (1) (2) (3) (4) (5) (6) (7) (8) (9) (10) (11) (12) • Structural Modeling (1) (2)
• Systems Science (1) (2)

Animated Logical Graphs • 61

Posted on February 26, 2021 by Jon Awbrey

Re: Richard J. Lipton • The Art Of Math
Re: Animated Logical Graphs • (57) • (58) • (59) • (60)

Anything called a duality is naturally associated with a transformation group of order 2, say a group $G$ acting on a set $X.$ Transformation groupies normally refer to $X$ as a set of “points” even when the elements have additional structure of their own, as they often do. A group of order two has the form $G = \{ 1, t \},$ where $1$ is the identity element and the remaining element $t$ satisfies the equation $t^2 = 1,$ being on that account self-inverse.

A first look at the dual interpretation of logical graphs from a group-theoretic point of view is provided by the following Table. The sixteen boolean functions $f : \mathbb{B} \times \mathbb{B} \to \mathbb{B}$ on two variables are listed in Column 1. Column 2 lists the elements of the set $X,$ specifically, the sixteen logical graphs $\gamma$ giving canonical expression to the boolean functions in Column 1. Column 2 shows the graphs in existential order but the order is arbitrary since only the transformations of the set $X$ into itself are material in this setting. Column 3 shows the result $1 \gamma$ of the group element $1$ acting on each graph $\gamma$ in $X,$ which is of course the same graph $\gamma$ back again. Column 4 shows the result $t \gamma$ of the group element $t$ acting on each graph $\gamma$ in $X,$ which is the entitative graph dual to the existential graph in Column 2.

$\text{Peirce Duality as Group Symmetry}$

The last Row of the Table displays a statistic of considerable interest to transformation group theorists. It is the total incidence of fixed points, in other words, the number of points in $X$ left invariant or unchanged by the respective group actions. I’ll explain the significance of the fixed point parameter next time.

Resources

Animated Logical Graphs • 60

Posted on February 21, 2021 by Jon Awbrey

Re: Laws of Form • Lyle Anderson
Re: Richard J. Lipton • The Art Of Math
Re: Animated Logical Graphs • (57) • (58) • (59)

LA:

Definition 1. A group $(G, *)$ is a set $G$ together with a binary operation $* : G \times G \to G$ satisfying the following three conditions.

Associativity. For any $x, y, z \in G,$ we have $(x * y) * z = x * (y * z).$
Identity. There is an identity element $e \in G$ such that $\forall g \in G,$
we have $e * g = g * e = g.$
Inverses. Each element has an inverse, that is, for each $g \in G,$
there is some $h \in G$ such that $g * h = h * g = e.$

Dear Lyle,

Thanks for supplying that definition of a mathematical group. It will afford us a wealth of useful concepts and notations as we proceed. As you know, the above three axioms define what is properly called an abstract group. Over the course of group theory’s history this definition was gradually abstracted from the more concrete examples of permutation groups and transformation groups initially arising in the theory of equations and their solvability.

As it happens, the application of group theory I’ll be developing over the next several posts will be using the more concrete type of structure, where a transformation group $G$ is said to “act on” a set $X$ by permuting its elements among themselves. In the work we do here, each group $G$ we contemplate will act a set $X$ which may be viewed as either one of two things, either a canonical set of expressions in a formal language or the mathematical objects denoted by those expressions.

What you say about deriving arithmetic, algebra, group theory, and all the rest from the calculus of indications may well be true, but it remains to be shown if so, and that’s a ways down the road from here.

Resources

Animated Logical Graphs • 59

Posted on February 21, 2021 by Jon Awbrey

Re: Richard J. Lipton • The Art Of Math
Re: Animated Logical Graphs • (57) • (58)

Returning to the theme of duality and more general group-theoretic symmetries in logical graphs, here’s an improved version of the introduction I gave two years ago.

Cf: Animated Logical Graphs • 30

The duality between Entitative and Existential interpretations of logical graphs is a good example of a mathematical symmetry, in this case a symmetry of order two. Symmetries of this and higher orders give us conceptual handles on excess complexity in the manifold of sensuous impressions, making it well worth the effort to seek them out and grasp them where we find them.

In that vein, here’s a Rosetta Stone to give us a grounding in the relationship between boolean functions and our two readings of logical graphs.

$\text{Boolean Functions on Two Variables}$

Resources

Double Negation • 3

Posted on February 19, 2021 by Jon Awbrey

Re: Double Negation • (1) • (2)

The steps of the proof of double negation are replayed in the following animation.

Resources

Reference

Spencer Brown, G. (1969), Laws of Form, George Allen and Unwin, London, UK.

cc: Cybernetics • Laws of Form • FB | Logical Graphs • Ontolog Forum • Peirce List
• Structural Modeling • Systems Science

Double Negation • 2

Posted on February 18, 2021 by Jon Awbrey

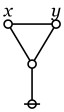
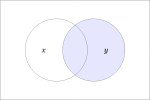
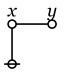
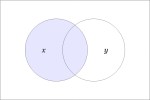
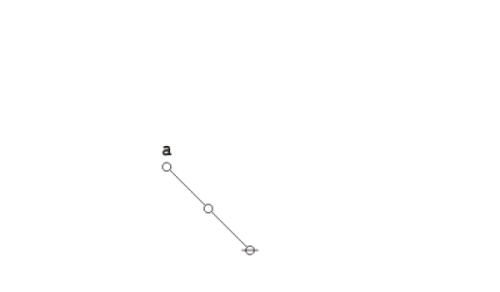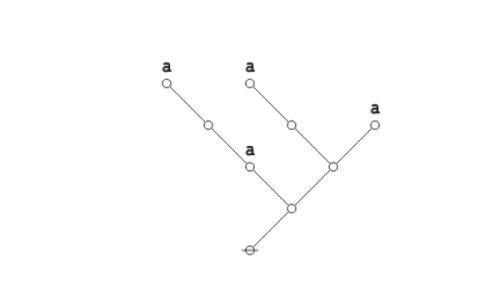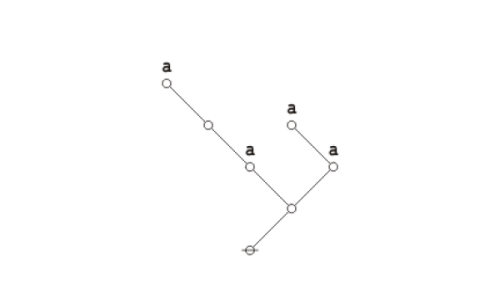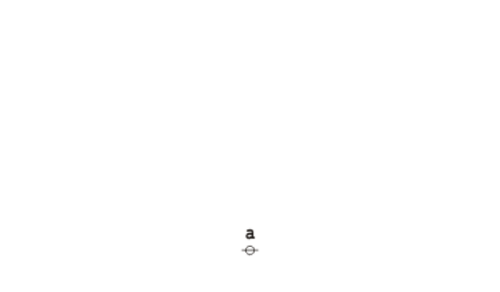
If we stand back for a moment to regard the structure of an implicational logic, such as Whitehead and Russell’s, we see that it is fully contained in that of an equivalence logic. The difference is in the kind of step used. In one case expressions are detached at the point of implication, in the other they are detached at the point of equivalence.

G. Spencer Brown • Laws of Form

We have been exploring the properties of a simple but elegant formal system exhibiting useful applications to logic. This very simplicity helps us focus on core features of formal systems and logical reasoning in a far less cluttered environment than the general run of logical systems. Earlier we touched on the theme of duality sourcing the radiation of mathematical form into logical subject matter, a theme we’ll touch on again.

But while we have the simple but critical example of Double Negation in our sights let’s use it to illustrate another central feature of logical graphs bearing on the mathematical infrastructure of logic. This is the power of using equational inference over and above implicational inference in proofs.

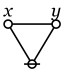
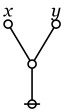
Here again is the formal equation corresponding to the principle of double negation, shown below in graph-theoretic and traversal-string forms.

Whether any principle is taken for an axiom or has to be proven as a theorem depends on the formal system at hand. In the present system double negation is a consequence of the following set of axioms.

Axioms

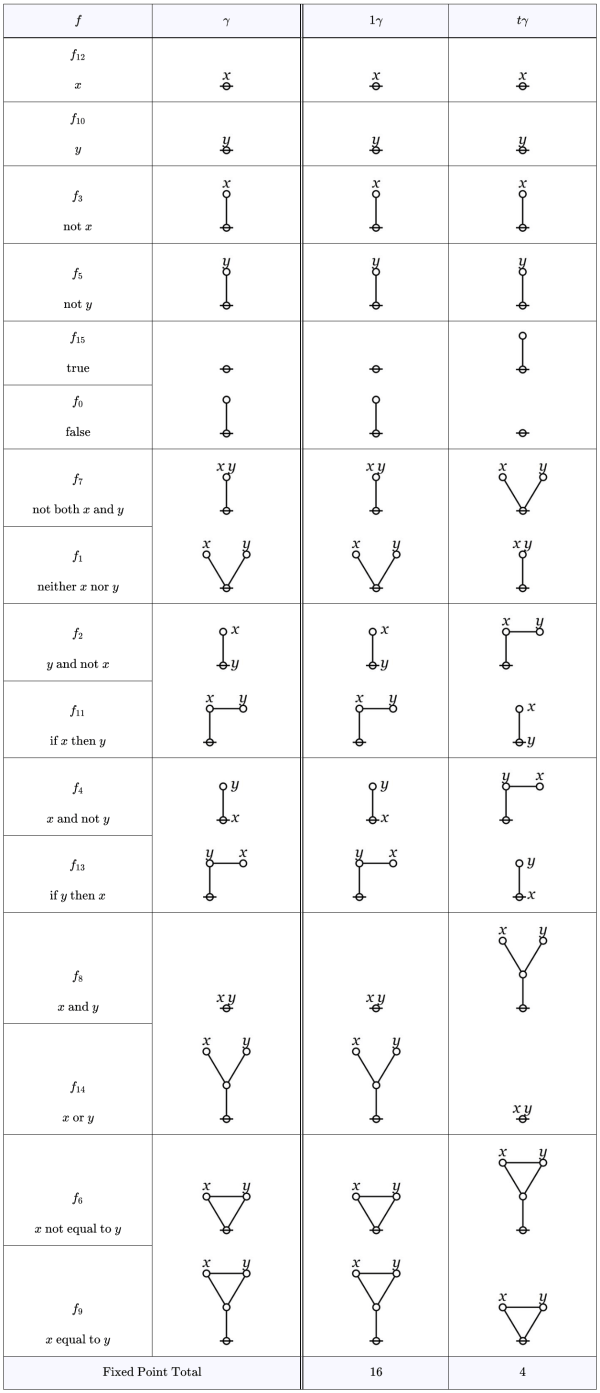
The formal system of logical graphs is defined by a foursome of formal equations, called initials when regarded purely formally, in abstraction from potential interpretations, and called axioms when interpreted as logical equivalences. There are two arithmetic initials and two algebraic initials, as shown below.

Arithmetic Initials

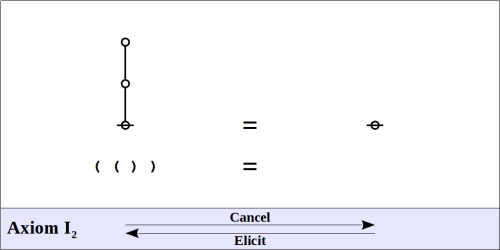
Algebraic Initials

Logical Interpretation

One way of assigning logical meaning to the initial equations is known as the entitative interpretation (En). Under En, the axioms read as follows.

$\begin{array}{ccccc} \mathrm{I_1} & : & \text{true} ~ \text{or} ~ \text{true} & = & \text{true} \\[4pt] \mathrm{I_2} & : & \text{not} ~ \text{true} & = & \text{false} \\[4pt] \mathrm{J_1} & : & a ~ \text{or} ~ \text{not} ~ a & = & \text{true} \\[4pt] \mathrm{J_2} & : & (a ~ \text{or} ~ b) ~ \text{and} ~ (a ~ \text{or} ~ c) & = & a ~ \text{or} ~ (b ~ \text{and} ~ c) \end{array}$

Another way of assigning logical meaning to the initial equations is known as the existential interpretation (Ex). Under Ex, the axioms read as follows.

$\begin{array}{ccccc} \mathrm{I_1} & : & \text{false} ~ \text{and} ~ \text{false} & = & \text{false} \\[4pt] \mathrm{I_2} & : & \text{not} ~ \text{false} & = & \text{true} \\[4pt] \mathrm{J_1} & : & a ~ \text{and} ~ \text{not} ~ a & = & \text{false} \\[4pt] \mathrm{J_2} & : & (a ~ \text{and} ~ b) ~ \text{or} ~ (a\ \text{and}\ c) & = & a ~ \text{and} ~ (b ~ \text{or} ~ c) \end{array}$

Equational Inference

Formal proofs in what follows employ a variation on Spencer Brown’s annotation scheme to mark each step of proof according to which axiom is called to license the corresponding step of syntactic transformation, whether it applies to graphs or to strings. All the axioms in the above set have the form of equations. This means the inference steps they license are all reversible. The proof annotation scheme employs a double bar $=\!=\!=\!=\!=\!=$ to mark this fact, though it will often be left to the reader to decide which of the two possible directions is the one required for applying the indicated axiom.

Here is the proof of Double Negation.

The actual business of proof is a far more strategic affair than the simple cranking of inference rules might suggest. Part of the reason for this lies in the circumstance that implicational inference rules combine the moving forward of a state of inquiry with the losing of whatever information along the way one did not think immediately relevant, at least, not as viewed in the local focus and short hauls of moment to moment progress of the proof in question. Over the long haul, this has the pernicious side-effect of one being strategically forced to reconstruct much of the information one had strategically thought to forget in earlier stages of the proof, where before the proof started may be counted as an earlier stage of the proof in view.

This is one of the reasons it is instructive to study equational inference rules. Equational forms of reasoning are paramount in mathematics but they are less familiar to the student of conventional logic textbooks, who may find a few surprises here.

Resources

Reference

Spencer Brown, G. (1969), Laws of Form, George Allen and Unwin, London, UK, p. 118.

cc: Cybernetics • Laws of Form • FB | Logical Graphs • Ontolog Forum • Peirce List
• Structural Modeling • Systems Science

Double Negation • 1

Posted on February 14, 2021 by Jon Awbrey

The article and section linked below introduce the Double Negation Theorem (DNT) in the manner described as Consequence 1 $(C_1)$ or Reflection by Spencer Brown.

Logical Graphs • Double Negation

Converting the planar figures used by Peirce and Spencer Brown to the graph-theoretic structures commonly used in mathematics and computer science, the double negation theorem takes the following form.

The formal system of logical graphs is defined by a foursome of formal equations, called initials when regarded purely formally, in abstraction from potential interpretations, and called axioms when interpreted as logical equivalences. There are two arithmetic initials and two algebraic initials, as shown below.

Arithmetic Initials

Algebraic Initials

Using these equations as transformation rules permits the development of formal consequences which may be interpreted as logical theorems. The double negation theorem is one such consequence. The proof of the double negation theorem I give next time is adapted from the one Spencer Brown presents in his Laws of Form and credits to two of his students, John Dawes and D.A. Utting.

Resources

Logic Syllabus
Logical Graphs • Informal Introduction • Formal Development

cc: Cybernetics • Laws of Form • FB | Logical Graphs • Ontolog Forum • Peirce List
• Structural Modeling • Systems Science

	Survey of Differenti… on Differential Logic • 5
	Differential Logic •… on Differential Logic • 4
	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…
	Differential Logic •… on Logic Syllabus
	Differential Logic •… on Differential Logic • 4
	Differential Logic •… on Survey of Animated Logical Gra…
	Differential Logic •… on Survey of Differential Logic •…
	Differential Logic •… on Logic Syllabus
	Survey of Differenti… on Differential Logic • 4

Resources

Share this:

Resources

Share this:

Resources

Share this:

Resources

Share this:

Resources

Share this:

Resources

Share this:

Resources

Share this:

Resources

Reference

Share this:

Axioms

Arithmetic Initials

Algebraic Initials

Logical Interpretation

Equational Inference

Resources

Reference

Share this:

Arithmetic Initials

Algebraic Initials

Resources

Share this:

Elsewhere

Blogroll

Follow Blog via Email

Recent Posts

Recent Comments

Archives

Blog Stats

Categories

Logic, Mathematics, Philosophy

Current Events

Meta