Sign Relational Manifolds • 5

Posted on November 6, 2022 by Jon Awbrey

Let me try to say in intuitive terms what I think is really going on here.

The problem we face is as old as the problem of other minds, or intersubjectivity, or even commensurability, and it naturally involves a whole slew of other old problems — reality and appearance, or reality and representation, not to mention the one and the many.  One way to sum up the question might be “conditions on the possibility of a mutually objective world”.

Working on what oftentimes seems like the tenuous assumption that there really is a real world causing the impressions in my mind and the impressions in yours — more generally speaking, that there really is a real world impressing itself in systematic measures on every frame of reference — we find ourselves pressed to give an account of the hypothetical unity beneath the manifest diversity — and how it is possible to discover the former in the latter.

Manifold theory proposes one type of solution to that host of problems.

cc: Conceptual Graphs • Cybernetics • Laws of Form • Ontolog Forum
cc: FB | Semeiotics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Cybernetics, Differential Geometry, Differential Logic, Geometry, Interoperability, Logic, Manifolds, Mathematics, Riemann, Semiotics, Sign Relational Manifolds, Sign Relations, Triadic Relations, Visualization | Tagged , , , , , , , , , , , , , , | 6 Comments

Sign Relational Manifolds • 4

Posted on November 5, 2022 by Jon Awbrey

Another set of notes I found on this theme strikes me as getting to the point more quickly and though they read a little rough in places I think it may be worth the effort to fill out their general line of approach.

cc: Conceptual Graphs • Cybernetics • Laws of Form • Ontolog Forum
cc: FB | Semeiotics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Cybernetics, Differential Geometry, Differential Logic, Geometry, Interoperability, Logic, Manifolds, Mathematics, Riemann, Semiotics, Sign Relational Manifolds, Sign Relations, Triadic Relations, Visualization | Tagged , , , , , , , , , , , , , , | 6 Comments

Sign Relational Manifolds • 3

Posted on November 3, 2022 by Jon Awbrey

I’m not sure when it was I first noticed the relationship between manifolds and semiotics but I distinctly recall the passage in Serge Lang’s Differential and Riemannian Manifolds which brought the triadic character of tangent vectors into high relief.  I copied out a set of excerpts highlighting the point and shared it with the Inquiry, Ontology, and Peirce lists.

Excerpts from Serge Lang, Differential and Riemannian Manifolds,
Springer‑Verlag, New York, NY, 1995.

Chapter 2.  Manifolds

Using the concepts and terminology from Lang’s text, I explained the connection between manifold theory and semiotics in the following way.

cc: Conceptual Graphs • Cybernetics • Laws of Form • Ontolog Forum
cc: FB | Semeiotics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Cybernetics, Differential Geometry, Differential Logic, Geometry, Intentionality, Logic, Manifolds, Mathematics, Riemann, Semiotics, Sign Relational Manifolds, Sign Relations, Triadic Relations, Visualization | Tagged , , , , , , , , , , , , , , | 6 Comments

Sign Relational Manifolds • 2

Posted on November 1, 2022 by Jon Awbrey

A sense of how manifolds are applied in practice may be gleaned from the set of excerpts linked below, from Doolin and Martin (1990), Introduction to Differential Geometry for Engineers, which I used in discussing differentiable manifolds with other participants in the IEEE Standard Upper Ontology Working Group.

What brought the concept of a manifold to mind in that context was a set of problems associated with perspectivity, relativity, and interoperability among multiple ontologies.  To my way of thinking, those are the very sorts of problems manifolds were invented to handle.

Reference

  • Doolin, Brian F., and Martin, Clyde F. (1990), Introduction to Differential Geometry for Engineers, Marcel Dekker, New York, NY.

cc: Conceptual Graphs • Cybernetics • Laws of Form • Ontolog Forum
cc: FB | Semeiotics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Cybernetics, Differential Geometry, Differential Logic, Geometry, Interoperability, Logic, Manifolds, Mathematics, Riemann, Semiotics, Sign Relational Manifolds, Sign Relations, Triadic Relations, Visualization | Tagged , , , , , , , , , , , , , , | 6 Comments

Sign Relational Manifolds • 1

Posted on October 31, 2022 by Jon Awbrey

Riemann’s concept of a manifold, especially as later developed, bears a close relationship to Peirce’s concept of a sign relation.

I will have to wait for my present train of thought to stop at a station before I can hop another but several recent discussions of geometry have brought the subject back to mind and I thought it might serve to drop off a few mail bags of related letters in anticipation of the next pass through this junction.

Here is a set of excerpts from Murray G. Murphey (1961), The Development of Peirce’s Philosophy, discussing Peirce’s reception of Riemann’s philosophy of geometry.

Later developments of the manifold concept, looking to applications on the one hand and theory on the other, are illustrated by excerpts in the next two posts.

cc: Conceptual Graphs • Cybernetics • Laws of Form • Ontolog Forum
cc: FB | Semeiotics • Structural Modeling • Systems Science

Posted in C.S. Peirce, Cybernetics, Differential Geometry, Differential Logic, Geometry, Interoperability, Logic, Manifolds, Mathematics, Riemann, Semiotics, Sign Relational Manifolds, Sign Relations, Triadic Relations, Visualization | Tagged , , , , , , , , , , , , , , | 6 Comments

Zeroth Law Of Semiotics • Discussion 2

Posted on October 27, 2022 by Jon Awbrey

Re: All Liar, No Paradox • Zeroth Law Of Semiotics
Re: FB | Charles S. Peirce Society • Joseph Harry

Paradoxes star among my first loves in logic.  So enamored was I with tricks of the mind’s eye I remember once concocting the motto, “Only what is paradoxical is ornery enough to exist”.  These days my less precocious self tends to suspect all our nominal paradoxes will gradually dissolve on sufficient inspection and placement in the proper light.  There I find the pragmatic spectrum of C.S. Peirce, stretching from the theory of triadic sign relations to the mathematical forms underlying logic, brings a full range of lights to the purpose.

It was by those lights, Peirce’s semiotic and logical graphs, I came to see through the fog of misdirection surrounding the so-called Liar Paradox, inscribing my epitaph to Epimenides under the heading “All Liar, No Paradox”.  More than that it became possible to see how the apparent paradox derives its appearance from unexamined assumptions about the relation between signs and objects.

That much prologue brings us up to speed with the Zeroth Law Of Semiotics and the scene of Joseph Harry’s remarks.

JH:
“Meaning is a privilege not a right” would seem to be a meaningless proposition, since ‘privilege’ and ‘right’ are third-order evaluative, symbolic terms, while ‘meaning’ is a neutral second-order term, implying only existential individualized dynamic activity or process.  Driving (a car) is a privilege not a right, but meaning is neither.

Dear Joseph,

That may be too literal a reading for Zero‑Aster’s poetic figure.  If I read the oracle right, the contrast between “privilege” and “right” serves merely to mark the distinction between meanings optional and obligatory.  Whether any hint of “private law” or “law unto itself” is intended or involved is something I would have to spend more time thinking about.

Regards,

Jon

cc: Conceptual Graphs • Cybernetics • Laws of Form (1) (2) • Ontolog Forum
cc: FB | Semeiotics • Peirce List (1) (2) (3) • Structural Modeling • Systems Science

Posted in Animata, C.S. Peirce, Denotation, Information = Comprehension × Extension, Liar Paradox, Logic, Logical Graphs, Mathematics, Nominalism, Pragmatic Maxim, Semiositis, Semiotics, Sign Relations, Zeroth Law Of Semiotics | Tagged , , , , , , , , , , , , , | 6 Comments

Abduction, Deduction, Induction, Analogy, Inquiry • 31

Posted on October 14, 2022 by Jon Awbrey

Re: Scott Aaronson • Explanation-Gödel and Plausibility-Gödel

Scott Aaronson asks a question arising from Gödel’s First Incompleteness Theorem, namely, what are its consequences for the differential values of explanation, plausibility, and proof?  I add the following thoughts.

A general heuristic in problem solving suggests priming the pump with a stronger hypothesis.  Applying that strategy here would have us broaden the grounds of validity, our notion of validation, from purely deductive proofs to more general forms of inference.  Along that line, and following a lead from Aristotle, C.S. Peirce recognized three distinct modes of inference, called abductive, deductive, and inductive reasoning, and that way of thinking has even had some traction in AI from the days of Warren S. McCulloch on.  At any rate I think it helps to view our questions in that ballpark.  There’s a budget of resources and running thoughts on the matter I keep on the following page.

cc: Conceptual Graphs • Cybernetics • Laws of Form • Ontolog Forum
cc: FB | Inquiry Driven Systems • Structural Modeling • Systems Science

Posted in Abduction, Analogy, Animata, Aristotle, Artificial Intelligence, C.S. Peirce, Deduction, Induction, Inquiry, Inquiry Driven Systems, Intelligent Systems Engineering, Logic, Mathematics, Scientific Method, Semiotics, Visualization | Tagged , , , , , , , , , , , , , , , | 5 Comments

Theme One Program • Exposition 8

Posted on October 8, 2022 by Jon Awbrey

Transformation Rules and Equivalence Classes

The abstract character of the cactus language relative to its logical interpretations makes it possible to give abstract rules of equivalence for transforming cacti among themselves and partitioning the space of cacti into formal equivalence classes.  The transformation rules and equivalence classes are “purely formal” in the sense of being indifferent to the logical interpretation, entitative or existential, one happens to choose.

Two definitions are useful here:

  • A reduction is an equivalence transformation which applies in the direction of decreasing graphical complexity.
  • A basic reduction is a reduction which applies to a basic connective, either a node connective or a lobe connective.

The two kinds of basic reductions are described as follows.

  • A node reduction is permitted if and only if every component cactus joined to a node itself reduces to a node.

Node Reduction

  • A lobe reduction is permitted if and only if exactly one component cactus listed in a lobe reduces to an edge.

Lobe Reduction

That is roughly the gist of the rules.  More formal definitions can wait for the day when we need to explain their use to a computer.

Resources

cc: Conceptual Graphs • Cybernetics • Laws of Form • Ontolog Forum
cc: FB | Theme One Program • Structural Modeling • Systems Science

Posted in Algorithms, Animata, Artificial Intelligence, Boolean Functions, C.S. Peirce, Cactus Graphs, Cognition, Computation, Constraint Satisfaction Problems, Data Structures, Differential Logic, Equational Inference, Formal Languages, Graph Theory, Inquiry Driven Systems, Laws of Form, Learning Theory, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Painted Cacti, Peirce, Propositional Calculus, Semiotics, Spencer Brown, Visualization | Tagged , , , , , , , , , , , , , , , , , , , , , , , , , , | 3 Comments

Theme One Program • Exposition 7

Posted on September 30, 2022 by Jon Awbrey

Mathematical Structure and Logical Interpretation

The main things to take away from the previous post are the following two ideas, one syntactic and one semantic.

  • Syntax.  The compositional structures of cactus graphs and cactus expressions are constructed from two kinds of connective operations.
  • Semantics.  There are two ways of mapping the compositional structures of syntax into the compositional structures of propositional sentences.

The two kinds of connective operations are described as follows.

  • The node connective joins a number of component cacti C_1, \ldots, C_k to a node, as shown below.

Node Connective

  • The lobe connective joins a number of component cacti C_1, \ldots, C_k to a lobe, as shown below.

Lobe Connective

The two ways of mapping cactus structures to logical meanings are summarized in Table 3, which compares the entitative and existential interpretations of the basic cactus structures, in effect, the graphical constants and connectives.

\text{Table 3. Logical Interpretations of Cactus Structures}
Logical Interpretations of Cactus Structures

Resources

cc: Conceptual Graphs • Cybernetics • Laws of Form • Ontolog Forum
cc: FB | Theme One Program • Structural Modeling • Systems Science

Posted in Algorithms, Animata, Artificial Intelligence, Boolean Functions, C.S. Peirce, Cactus Graphs, Cognition, Computation, Constraint Satisfaction Problems, Data Structures, Differential Logic, Equational Inference, Formal Languages, Graph Theory, Inquiry Driven Systems, Laws of Form, Learning Theory, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Painted Cacti, Peirce, Propositional Calculus, Semiotics, Spencer Brown, Visualization | Tagged , , , , , , , , , , , , , , , , , , , , , , , , , , | 3 Comments

Theme One Program • Exposition 6

Posted on September 29, 2022 by Jon Awbrey

Quickly recapping the discussion so far, we started with a data structure called an idea‑form flag and adopted it as a building block for constructing a species of graph-theoretic data structures called painted and rooted cacti.  We showed how to code the abstract forms of cacti into character strings called cactus expressions and how to parse the character strings into pointer structures in computer memory.

At this point we had to choose between two expository strategies.

A full account of Theme One’s operation would describe its use of cactus graphs in three distinct ways, called lexical, literal, and logical applications.  The more logical order would approach the lexical and literal tasks first.  That is because the program’s formal language learner must first acquire the vocabulary its propositional calculator interprets as logical variables.  The sequential learner operates at two levels, taking in sequences of characters it treats as strings or words plus sequences of words it treats as strands or sentences.

Finding ourselves more strongly attracted to the logical substance, however, we leave the matter of grammar to another time and turn to Theme One’s use of cactus graphs in its reasoning module to represent logical propositions on the order of Peirce’s alpha graphs and Spencer Brown’s calculus of indications.

Logical Cacti

Up till now we’ve been working to hammer out a two-edged sword of syntax, honing the syntax of cactus graphs and cactus expressions and turning it to use in taming the syntax of two-level formal languages.

But the purpose of a logical syntax is to support a logical semantics, which means, for starters, to bear interpretation as sentential signs capable of denoting objective propositions about a universe of objects.

One of the difficulties we face is that the words interpretation, meaning, semantics, and their ilk take on so many different meanings from one moment to the next of their use.  A dedicated neologician might be able to think up distinctive names for all the aspects of meaning and all the approaches to them that concern us, but I will do the best I can with the common lot of ambiguous terms, leaving it to context and intelligent interpreters to sort it out as much as possible.

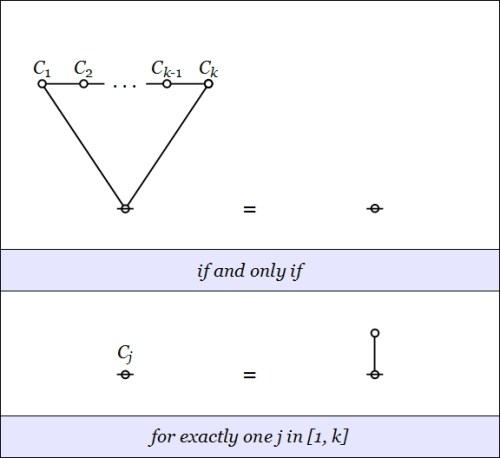
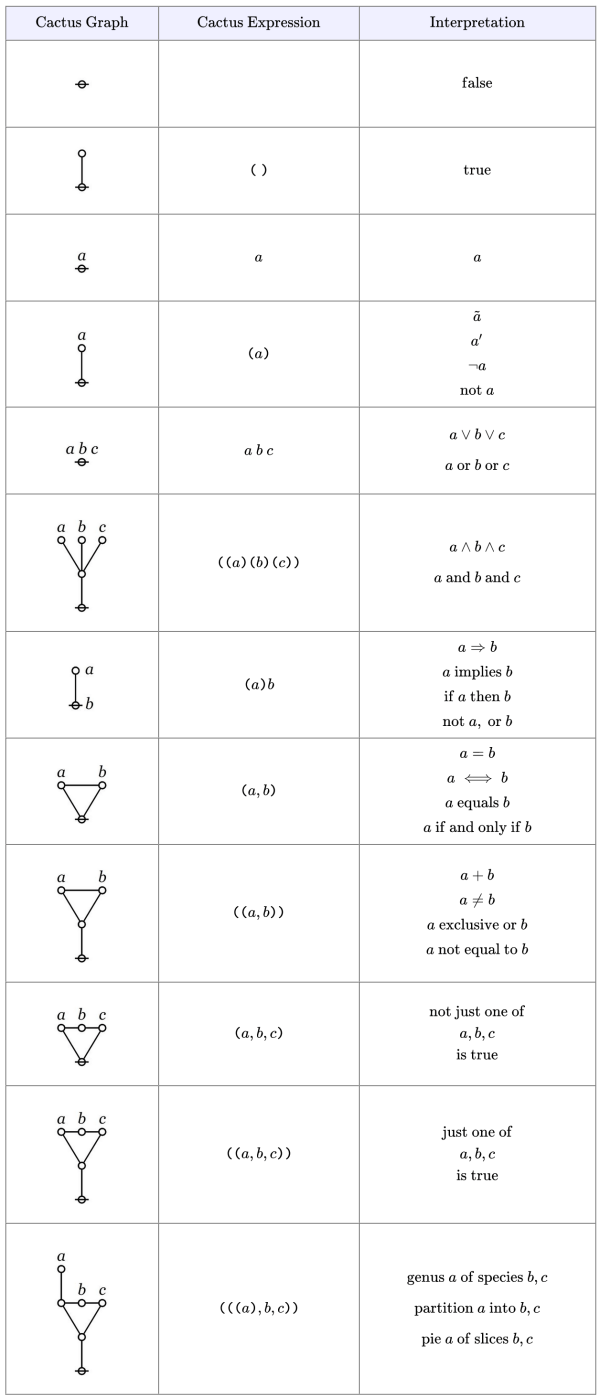
The formal language of cacti is formed at such a high level of abstraction that its graphs bear at least two distinct interpretations as logical propositions.  The two interpretations concerning us here are descended from the ones C.S. Peirce called the entitative and the existential interpretations of his systems of graphical logics.

Existential Interpretation

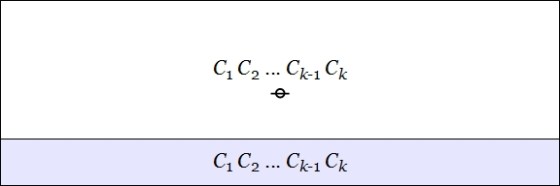
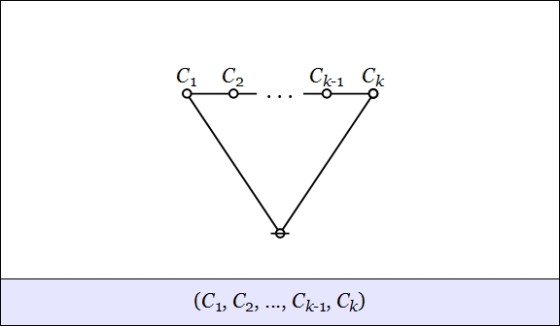
Table 1 illustrates the existential interpretation of cactus graphs and cactus expressions by providing English translations for a few of the most basic and commonly occurring forms.

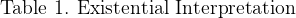
\text{Table 1. Existential Interpretation}
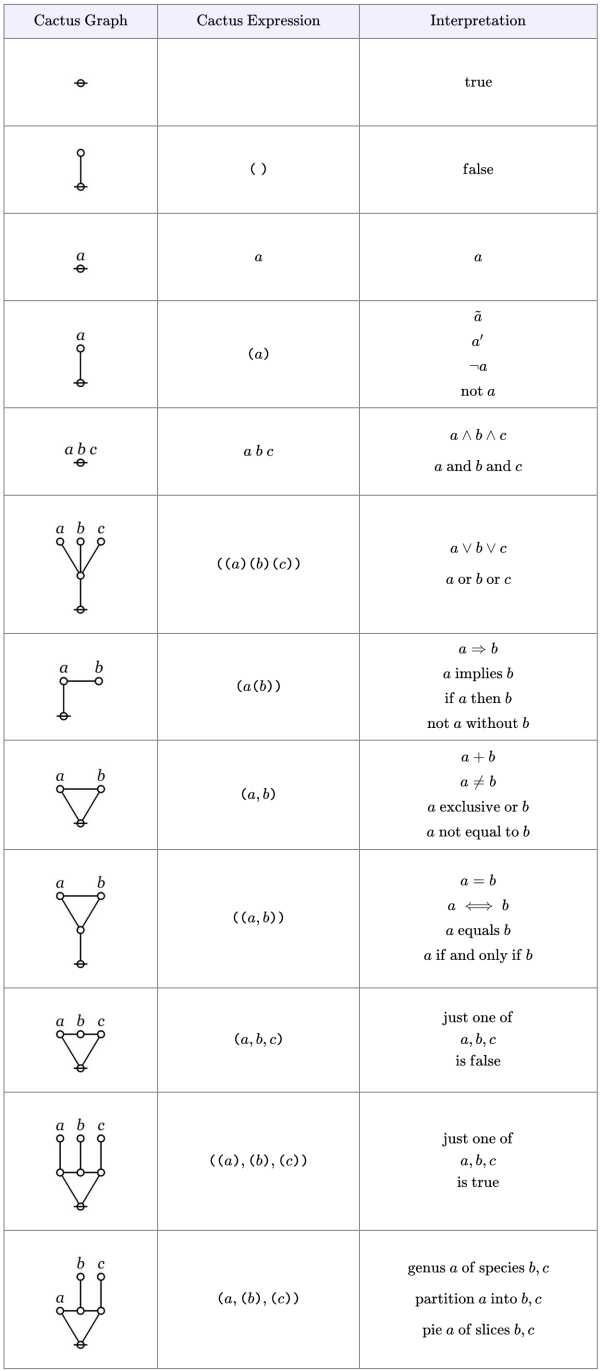
Existential Interpretation

Entitative Interpretation

Table 2 illustrates the entitative interpretation of cactus graphs and cactus expressions by providing English translations for a few of the most basic and commonly occurring forms.

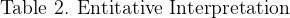
\text{Table 2. Entitative Interpretation}
Entitative Interpretation

Resources

cc: Conceptual Graphs • Cybernetics • Laws of Form • Ontolog Forum
cc: FB | Theme One Program • Structural Modeling • Systems Science

Posted in Algorithms, Animata, Artificial Intelligence, Boolean Functions, C.S. Peirce, Cactus Graphs, Cognition, Computation, Constraint Satisfaction Problems, Data Structures, Differential Logic, Equational Inference, Formal Languages, Graph Theory, Inquiry Driven Systems, Laws of Form, Learning Theory, Logic, Logical Graphs, Mathematics, Minimal Negation Operators, Painted Cacti, Peirce, Propositional Calculus, Semiotics, Spencer Brown, Visualization | Tagged , , , , , , , , , , , , , , , , , , , , , , , , , , | 5 Comments