Inquiry Into Inquiry

Logical Cacti (cont.)

The abstract character of the cactus language relative to its logical interpretations makes it possible to give abstract rules of equivalence for transforming cacti among themselves and partitioning the space of cacti into formal equivalence classes.  The transformation rules and equivalence classes are “purely formal” in the sense of being indifferent to the logical interpretation, entitative or existential, one happens to choose.

Two definitions are useful here:

• A reduction is an equivalence transformation which applies in the direction of decreasing graphical complexity.
• A basic reduction is a reduction which applies to a basic connective, either a node connective or a lobe connective.

The two kinds of basic reductions are described as follows.

• A node reduction is permitted if and only if every component cactus joined to a node itself reduces to a node.

• A lobe reduction is permitted if and only if exactly one component cactus listed in a lobe reduces to an edge.

That is roughly the gist of the rules.  More formal definitions can wait for the day when we have to explain all this to a computer.

Resources

• Theme One Program • Overview
• Theme One Program • Exposition
• Theme One Program • User Guide

cc: Peirce List • (1) • (2) • (3)

Logical Cacti (cont.)

The main things to take away from the previous post are the following two ideas, one syntactic and one semantic.

• The compositional structures of cactus graphs and cactus expressions are constructed from two kinds of connective operations.
• There are two ways of mapping these compositional structures into the compositional structures of propositional sentences.

The two kinds of connective operations are described as follows.

• The node connective joins a number of component cacti to a node:

• The lobe connective joins a number of component cacti to a lobe:

The two ways of mapping cactus structures to logical meanings are summarized in Table 3, which compares the entitative and existential interpretations of the basic cactus structures, in effect, the graphical constants and connectives.

Resources

• Theme One Program • Overview
• Theme One Program • Exposition
• Theme One Program • User Guide

cc: Peirce List • (1) • (2) • (3)

The portions of exposition just skipped over covered the use of cactus graphs in the program’s learning module to learn sequences of characters called “words” or “strings” and sequences of words called “sentences” or “strands”.  Leaving the matter of grammar to another time we turn to the use of cactus graphs in the program’s reasoning module to represent logical propositions on the order of Peirce’s alpha graphs and Spencer Brown’s calculus of indications.

Logical Cacti

Up till now we’ve been working to hammer out a two-edged sword of syntax, honing the syntax of cactus graphs and cactus expressions and turning it to use in taming the syntax of two-level formal languages.

But the purpose of a logical syntax is to support a logical semantics, which means, for starters, to bear interpretation as sentential signs capable of denoting objective propositions about a universe of objects.

One of the difficulties we face is that the words interpretation, meaning, semantics, and their ilk take on so many different meanings from one moment to the next of their use.  A dedicated neologician might be able to think up distinctive names for all the aspects of meaning and all the approaches to them that concern us, but I will do the best I can with the common lot of ambiguous terms, leaving it to context and intelligent interpreters to sort it out as much as possible.

The formal language of cacti is formed at such a high level of abstraction that its graphs bear at least two distinct interpretations as logical propositions.  The two interpretations concerning us here are descended from the ones C.S. Peirce called the entitative and the existential interpretations of his systems of graphical logics.

Existential Interpretation

Table 1 illustrates the existential interpretation of cactus graphs and cactus expressions by providing English translations for a few of the most basic and commonly occurring forms.

Entitative Interpretation

Table 2 illustrates the entitative interpretation of cactus graphs and cactus expressions by providing English translations for a few of the most basic and commonly occurring forms.

Resources

• Theme One Program • Overview
• Theme One Program • Exposition
• Theme One Program • User Guide

cc: Peirce List • (1) • (2)

Re: Laws Of Form • Armahedi Mahzar

AM:  Why do you need XOR in your inquiry system?

Clearly we need a way to represent exclusive disjunction, along with its dual, logical equivalence, in any calculus capable of covering propositional logic, so I assume this is a question about why I chose to represent those two operations more compactly with cactus graphs instead of using trees and defining them in terms of conjunctions and negations.

The generalization from trees to cacti presented itself at the point where multiple lines of problem-solving effort converged.  Some of the problems were conceptual, arising from a desire to include the types of operator-variables Peirce considered.  Other problems were computational, provoked by a need to avoid combinatorial explosions in the evaluation of logical formulas.

But, as I remarked earlier, “the genesis of that generalization is a tale worth telling another time”, after we’ve gotten a better handle on the basic logical issues.

Resources

• Theme One Program • Overview
• Theme One Program • Exposition
• Survey of Theme One Program

cc: Cybernetics • Ontolog Forum (1) (2) • Systems Science (1) (2)
cc: Peirce List (12-12) (18-02) (18-03) (20-09) (20-10) (21-10)
cc: FB | Theme One Program • Laws of Form (1) (2)

Lexical, Literal, Logical

Theme One puts cactus graphs to work in three distinct but related ways, called lexical, literal, and logical applications.  The three modes of operation employ three distinct but overlapping subsets of the broader species of cacti.  Accordingly we find ourselves working with graphs, expressions, and files of lexical, literal, and logical types, depending on the task at hand.

The logical class of cacti is the broadest, encompassing the whole species described above, of which we have already seen a typical example in its several avatars as abstract graph, pointer data structure, and string of characters suitable for storage in a text file.

Being a logical cactus is not just a matter of syntactic form — it means being subject to meaningful interpretations as a sign of a logical proposition.  To enter the logical arena cactus expressions must express something, a proposition true or false of something.

Fully addressing the logical, interpretive, semantic aspect of cactus graphs normally requires a mind-boggling mass of preliminary work on the details of their syntactic structure.  Practical, pragmatic, and especially computational considerations will eventually make that unavoidable.  For the sake of the present discussion, however, let’s put that on hold and fast forward to the logical substance.

Resources

• Theme One Program • Overview
• Theme One Program • Exposition
• Theme One Program • User Guide

cc: Peirce List • (1) • (2)

We have seen how to take an abstract logical graph of a sort a person might have in mind to represent a logical state of affairs and translate it into a string of characters a computer can translate into a concrete data structure.

Now we look a little more closely at the finer details of those data structures, as they work out in this particular sequence of representations.

Parsing Logical Graphs

It is possible to write a program that parses cactus expressions into reasonable facsimiles of cactus graphs as pointer structures in computer memory, making edges correspond to addresses and nodes correspond to records.  I did just that in the early forerunners of the present program, but it turned out to be a more robust strategy in the long run, despite the need for additional nodes at the outset, to implement a more articulate but more indirect parsing algorithm, one in which the punctuation marks are not just tacitly converted to addresses in passing, but instead recorded as nodes in roughly the same way as the ordinary identifiers, or paints.

Figure 3 illustrates the type of parsing paradigm used by the program, showing the pointer graph structure obtained by parsing the cactus expression in Figure 2.  A traversal of this graph naturally reconstructs the cactus string that parses into it.

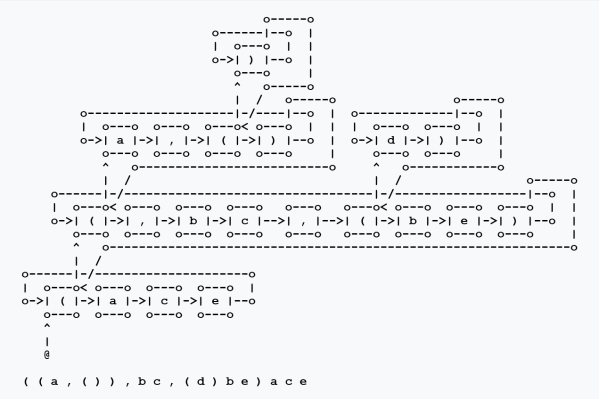
The pointer graph in Figure 3, namely, the parse graph of a cactus expression, is the sort of thing we’ll probably not be able to resist calling a cactus graph, for all the looseness of that manner of speaking, but we should keep in mind its level of abstraction lies a step further in the direction of a concrete implementation than the last thing we called by that name.  While we have them before our mind’s eyes, there are several other distinctive features of cactus parse graphs we ought to notice before moving on.

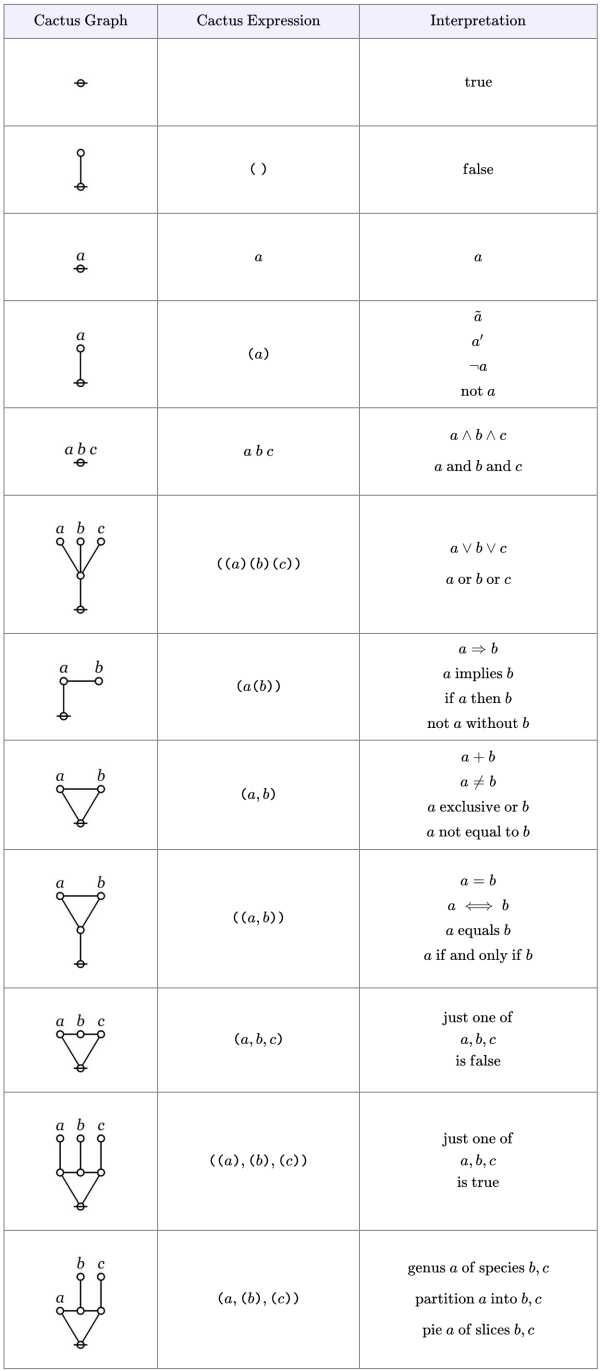
In terms of idea-form structures, a cactus parse graph begins with a root idea pointing into a by‑cycle of forms, each of whose sign fields bears either a paint, in other words, a direct or indirect identifier reference, or an opening left parenthesis indicating a link to a subtended lobe of the cactus.

A lobe springs from a form whose sign field bears a left parenthesis.  That stem form has an on idea pointing into a by‑cycle of forms, exactly one of which has a sign field bearing a right parenthesis.  That last form has an on idea pointing back to the form bearing the initial left parenthesis.

In the case of a lobe, aside from the single form bearing the closing right parenthesis, the by‑cycle of a lobe may list any number of forms, each of whose sign fields bears either a comma, a paint, or an opening left parenthesis signifying a link to a more deeply subtended lobe.

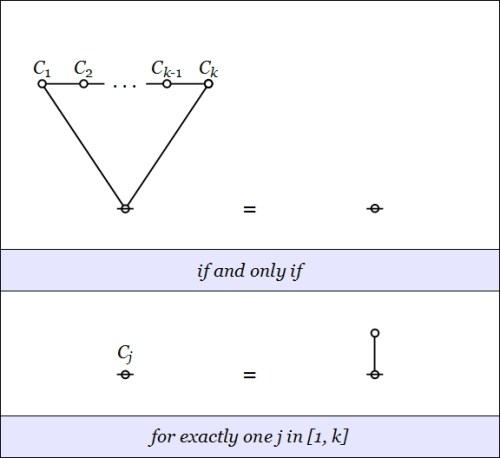
Just to draw out one of the implications of this characterization and to stress the point of it, the root node can be painted and bear many lobes, but it cannot be segmented, that is, the by‑cycle corresponding to the root node can bear no commas.

Resources

• Theme One Program • Overview
• Theme One Program • Exposition
• Theme One Program • User Guide

cc: Peirce List • (1) • (2)

Coding Logical Graphs

My earliest experiments coding logical graphs as dynamic “pointer” data structures taught me that conceptual and computational efficiencies of a critical sort could be achieved by generalizing their abstract graphs from trees to the variety graph theorists know as cacti.  The genesis of that generalization is a tale worth telling another time, but for now it’s best to jump right in and proceed by way of generic examples.

Figure 1 shows a typical example of a painted and rooted cactus.

Figure 2 shows a way to visualize the correspondence between cactus graphs and cactus strings, demonstrated on the cactus from Figure 1.  By way of convenient terminology, the polygons of a cactus graph are called its lobes.  An edge not part of a larger polygon is called a 2‑gon or a bi‑gon.  A terminal bi‑gon is called a spike.

The correspondence between a cactus graph and a cactus string is obtained by an operation called traversing the graph in question.

• One traverses a cactus graph by beginning at the left hand side of the root node, reading off the list of paints one encounters at that point.  Since the order of elements at any node is not significant, one may start the cactus string with that list of paints or save them for the end.  We have done the latter in this case.
• One continues by climbing up the left hand side of the leftmost lobe, marking the ascent by means of a left parenthesis, traversing whatever cactus one happens to reach at the first node above the root, that done, proceeding from left to right along the top side of the lobe, marking each interlobal span by means of a comma, traversing each cactus in turn one meets along the way, on completing the last of them climbing down the right hand side of the lobe, marking the descent by means of a right parenthesis, and then traversing each cactus in turn, in left to right order, that is incident with the root node.

The string of letters, parentheses, and commas one obtains by this procedure is called the traversal string of the graph, in this case, a cactus string.

Resources

• Theme One Program • Overview
• Theme One Program • Exposition
• Theme One Program • User Guide

cc: Peirce List • (1) • (2)

Re: Peirce List • (1) • (2)

Discussion arose in the Laws Of Form Group about computational explorations of George Spencer Brown’s calculus of indications.

Readers of Peirce are generally aware Spencer Brown revived certain aspects of Peirce’s logical graphs, focusing on what Peirce called the Alpha level and its interpretation for Boolean Algebra and Propositional Calculus but adding hints of potential extension and generalization.  Spencer Brown used what amounts to Peirce’s entitative interpretation of the graphical forms in his exposition but he was clear about the abstract character of the forms themselves, as evidenced by their dual interpretations, dubbed entitative and existential by Peirce.

In computational contexts the question naturally arises how to code the abstract formal structures used by the calculi of CSP and GSB into the relatively concrete forms that a computer can process.

I began my response to that question as follows …

• Theme One • A Program Of Inquiry 6

To be continued …

Resources

• Theme One Program • Overview
• Theme One Program • Exposition

Programs are algorithms operating on data structures (Niklaus Wirth).  How do we turn abstract graphs like those used by Charles S. Peirce and G. Spencer Brown into concrete data structures algorithms can manipulate?  There are many ways to do this, but one very efficient way is through the use of “pointer data structures”.

The full documentation of my Theme One Program is still in progress, but here’s a link to a page of exposition, describing the family of graphs used in the program, how to code the graphs as strings of parentheses, commas, and letters, and how the program parses the strings into pointer structures that live in computer memory.

• Theme One Program • Exposition

Here’s a link to a suitable point of entry for our present purpose:

• Theme One Program • Expository Note 2

       o
   a   |       d
   o---o       o
    \ /  b c   |
     o----o----o b e
      \       /
       \     /
        \   /
         \ /
          @ a c e

   Figure 1.  Painted And Rooted Cactus

Resources

• Theme One Program • Overview
• Theme One Program • Exposition
• Theme One Program • Expository Note 2