Re: Laws of Form • James Bowery

The concepts of closure and idempotence are closely related.

We usually speak of a closure operator in contexts where the objects acted on are the primary interest, as in topology, where the objects of interest are open sets, boundaries, closed sets, etc.  In contexts where we abstract away from the operand space, as in algebra, we tend to say idempotence for the detached application   (If I recall right, it was actually Charles Peirce’s father Benjamin who coined the term idempotence.)

At any rate, I’ll have to mutate the principle a bit to cover the uses Peirce makes of it.

cc: Systems Science • Structural Modeling • Ontolog Forum • Laws of Form • Cybernetics

Re: Structural Modeling • Joseph Simpson
Re: Peirce’s 1870 Logic Of Relatives • Selection 1

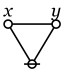
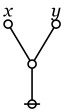
A critical question in mathematical logic and its applications concerns the threshold of complexity between dyadic (binary) and triadic (ternary) relations, in essence, whether 2-place relations are universally adequate or whether 3-place relations are irreducible, minimally adequate, and even sufficient as a basis for all higher dimensions.

One of Peirce’s earliest arguments for the sufficiency of triadic relative terms occurs at the top of his 1870 “Logic of Relatives”.

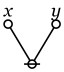
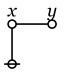
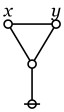
The conjugative term involves the conception of third, the relative that of second or other, the absolute term simply considers an object.  No fourth class of terms exists involving the conception of fourth, because when that of third is introduced, since it involves the conception of bringing objects into relation, all higher numbers are given at once, inasmuch as the conception of bringing objects into relation is independent of the number of members of the relationship.  Whether this reason for the fact that there is no fourth class of terms fundamentally different from the third is satisfactory or not, the fact itself is made perfectly evident by the study of the logic of relatives.  (Peirce, CP 3.63).

Peirce’s argument invokes what is known as a closure principle, as I remarked in the following comment:

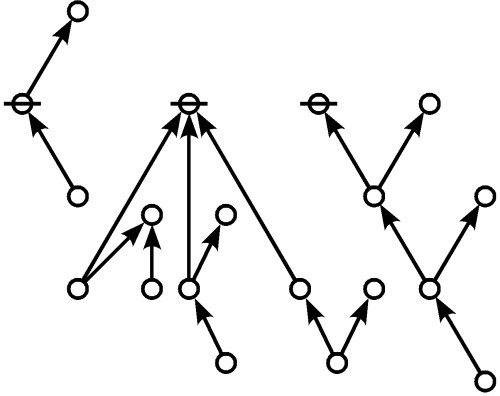
What strikes me about the initial installment this time around is its use of a certain pattern of argument I can recognize as invoking a closure principle, and this is a figure of reasoning Peirce uses in three other places:  his discussion of continuous predicates, his definition of sign relations, and in the formulation of the pragmatic maxim itself.

In mathematics, a closure operator is one whose repeated application yields the same result as its first application.

If we consider an arbitrary operator 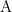, the result of applying 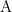to an operand is the result of applying 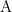again is the result of applying 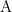again is and so on.  In general, it is perfectly possible each application yields a novel result, distinct from all previous results.

But a closure operator 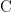is defined by the property so nothing new results beyond the first application.

cc: Systems Science • Structural Modeling • Ontolog Forum • Laws of Form • Cybernetics

Peirce Society Facebook Page • JC • JA • JA • JA • JC

A discussion — well, more like a series of posts and counterposts — arose last week on the Facebook Page of the Charles S. Peirce Society, and I’ve been going back over it this week because it seemed to invite a useful re-examination of some old but important issues.  There appears to be some sort of disagreement, or maybe just failure to communicate, but I’m still having trouble putting my finger on what the source of the issue might be.

One factor seems to be different understandings about the relationship between Peirce’s brand of semiotics and standard first order logic.  One thing I’ve noticed before is that people who view Peirce’s work through the filter of first order logic are not likely to see what many of us appreciate in his semiotic approach to logic.  There are commentators on Peirce’s logical systems who treat them as nothing more than first order logics in other syntaxes, but I am not one of those.  There is something more general and powerful going on with Peirce’s conception of “logic as formal semiotic”, in other words, a normative science of signs.

I still see that factor playing a role in the background of the animadversion but I’m beginning to think there’s probably a much simpler explanation.

cc: Systems Science • Structural Modeling • Ontolog Forum • Laws of Form • Cybernetics

Re: Ontolog Forum • John Bottoms
Re: The Difference That Makes A Difference That Peirce Makes : 20

The reflections in my previous blog post developed over several weeks observing various discussions around the web where people seemed to be spending most of their effort talking past each other and hardly ever getting any ideas or information out of one skull and into another.  It’s not the first time I’ve noticed belief systems, comfort zones, conceptual silos, paradigms, whatever we call them, acting like immune systems, insulating our mental metabolisms from intellectual antigens.

Anyhow, it’s a working hypothesis to prime future inquiry …

As far as Peirce references go, the choices are legion, so I’ll just link to one place I have in mind at the moment where Peirce sets out a number of truly radical ideas, ones I view as missed opportunities — so far as I know he never fully followed up on them.

• Peirce’s 1870 Logic Of Relatives
• Overview
• Part 1
• Part 2
• Part 3
• References
• Resources

cc: Systems Science • Structural Modeling • Ontolog Forum • Laws of Form • Cybernetics

cc: Systems Science • Structural Modeling • Ontolog Forum • Laws of Form • Cybernetics