Inquiry and Analogy • Application of Higher Order Propositions to Quantification Theory

Last time we took up a fourfold scheme of quantified propositional forms traditionally known as a “Square of Opposition”, relating it to a quartet of higher order propositions which, depending on context, are also known as measures, qualifiers, or higher order indicator functions.

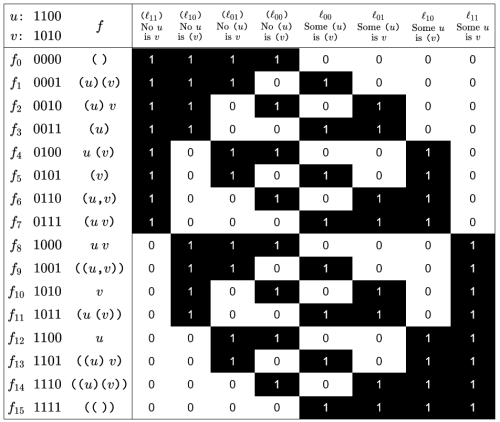
Table 18 develops the above ideas in further detail, expressing a larger set of quantified propositional forms by means of propositions about propositions.

Resources

• Logic Syllabus
• Boolean Function
• Boolean-Valued Function
• Logical Conjunction
• Minimal Negation Operator
• Introduction to Inquiry Driven Systems
• Functional Logic • Part 1 • Part 2 • Part 3
• Cactus Language • Part 1 • Part 2 • Part 3 • References • Document History

cc: FB | Peirce Matters • Laws of Form • Mathstodon • Ontolog • Academia.edu
cc: Conceptual Graphs • Cybernetics • Structural Modeling • Systems Science