Re: C.S. Peirce • Relatives of Second Intention
Re: Paradisaical Logic and the After Math • Comment (1) (2)
I am getting a feeling I occasionally get when discussing Peirce’s work in a group setting — as though we had a grand feast set before us while the dining philosophers wrangle over the amuse-bouche. With that in mind I’d like to return to the inciting text, the one so exciting me all those years ago, and see what’s truly substantial and tantalizing in it.
Selections from C.S. Peirce, “The Logic of Relatives”, CP 3.456–552
488. The general method of graphical representation of propositions has now been given in all its essential elements, except, of course, that we have not, as yet, studied any truths concerning special relatives; for to do so would seem, at first, to be “extralogical”.
Logic in this stage of its development may be called paradisaical logic, because it represents the state of Man’s cognition before the Fall. For although, with this apparatus, it is easy to write propositions necessarily true, it is absolutely impossible to write any which is necessarily false, or, in any way which that stage of logic affords, to find out that anything is false. The mind has not as yet eaten of the fruit of the Tree of Knowledge of Truth and Falsity.
Probably it will not be doubted that every child in its mental development necessarily passes through a stage in which he has some ideas, but yet has never recognised that an idea may be erroneous; and a stage that every child necessarily passes through must have been formerly passed through by the race in its adult development. It may be doubted whether many of the lower animals have any clear and steady conception of falsehood; for their instincts work so unerringly that there is little to force it upon their attention. Yet plainly without a knowledge of falsehood no development of discursive reason can take place.
489. This paradisaical logic appears in the study of non-relative formal logic. But there no possible avenue appears by which the knowledge of falsehood could be brought into this Garden of Eden except by the arbitrary and inexplicable introduction of the Serpent in the guise of a proposition necessarily false. The logic of relatives affords such an avenue, and that, the very avenue by which in actual development, this stage of logic supervenes. It is the avenue of experience and logical reflexion.
490. By logical reflexion, I mean the observation of thoughts in their expressions. Aquinas remarked that this sort of reflexion is requisite to furnish us with those ideas which, from lack of contrast, ordinary external experience fails to bring into prominence. He called such ideas second intentions. Is is by means of relatives of second intention that the general method of logical representation is to find completion.
Reference
- Charles S. Peirce, “The Logic of Relatives”, The Monist, vol. 7, 161–217, (1897). Reprinted, CP 3.456–552.
cc: Cybernetics • Ontolog Forum • Peirce List • Structural Modeling • Systems Science
cc: FB | Relation Theory • FB | Medieval Logic • Laws of Form
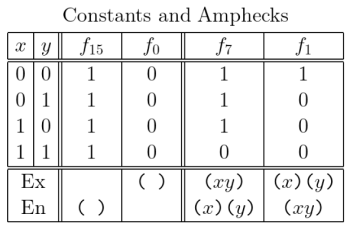
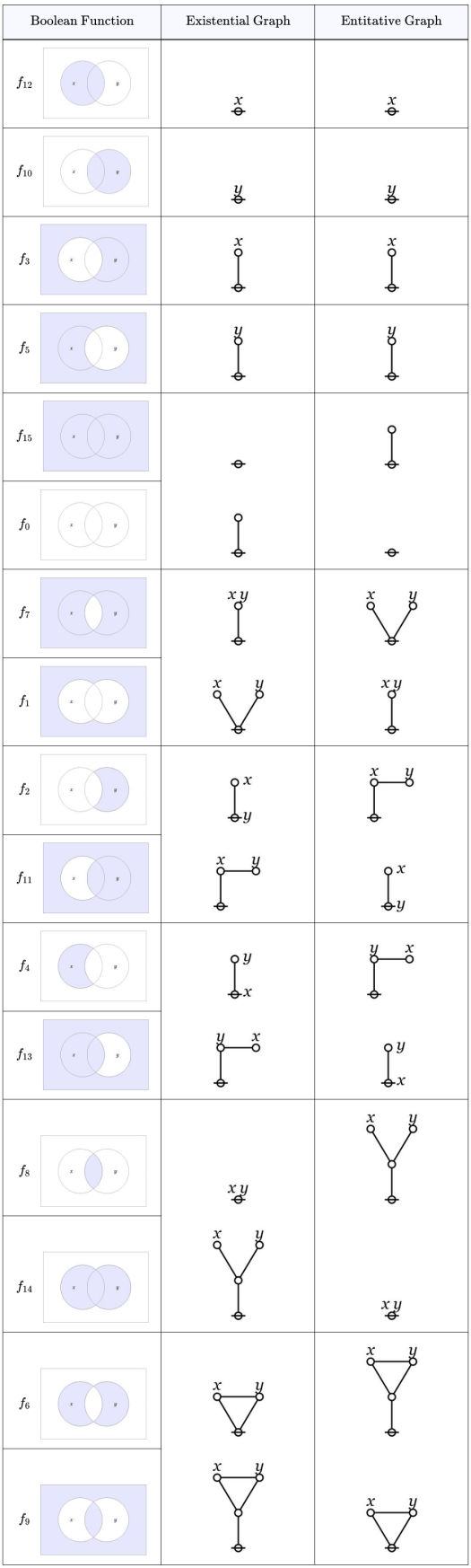
and
are dual to each other.
and
are dual to each other.
and the text expressions for their logical graphs are given in the following Table.